2015-2016学年山东省济宁市嘉祥县八年级下学期期中数学试卷
试卷更新日期：2016-10-13 类型：期中考试
一、选择题
-
1. 若式子 在实数范围内有意义，则x的取值范围是（ ）A、x≥1 B、x＞1 C、x＜1 D、x≤12.
如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是（ ）
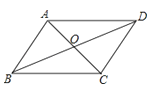A、AB∥CD B、AB=CD C、AC=BD D、OA=OC3. 下列二次根式中，最简二次根式是（ ）A、 B、 C、 D、4. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（ ）A、 ， ， B、2，3，4 C、6，7，8 D、1， ，5. 如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是（ ）
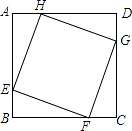A、30 B、34 C、36 D、406. 已知直角三角形的周长为4+ ， 斜边为4，则该三角形的面积是（ ）A、2 B、 C、 D、7. 分别顺次连接①平行四边形；②矩形；③菱形；④对角线相等的四边形“各边中点所构成的四边形”中，为菱形的是（ ）A、①② B、①③ C、②③ D、②④8. 已知a= +2，b=2﹣ ，则a2016b2015的值为（ ）A、﹣ ﹣2 B、﹣ +2 C、1 D、﹣19.如图：一个长、宽、高分别为4cm、3cm、12cm的长方体盒子能容下的最长木棒长为（ ）
A、11cm B、12cm C、13cm D、14cm10. 如图，在△ABC中，∠ACB=90°，D是BC的中点，DE⊥BC，CE∥AD，若AC=2，∠ADC=30°，①四边形ACED是平行四边形；
②△BCE是等腰三角形；
③四边形ACEB的周长是10+2 ；
④四边形ACEB的面积是16．
则以上结论正确的是（ ）
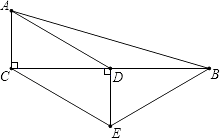A、①②③ B、①②④ C、①③④ D、②④二、填空题
-
11. 已知最简二次根式 与2 可以合并，则a的值是 ．12. 如图，矩形内有两个相邻的正方形，面积分别为4和2，那么阴影部分的面积是 ．
13. 如图，矩形ABCD的对角线AC、BD相交于点O，∠AOB=120°，CE∥BD，DE∥AC，若AD=4，则四边形CODE的周长 ．
14. 如图，小华将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8m处，发现此时绳子末端距离地面2m，则旗杆的高度为 ．
15. 观察下列勾股数第一组：3=2×1+1，4=2×1×（1+1），5=2×1×（1+1）+1
第二组：5=2×2+1，12=2×2×（2+1），13=2×2×（2+1）+1
第三组：7=2×3+1，24=2×3×（3+1），25=2×3×（3+1）+1
第四组：9=2×4+1，40=2×4×（4+1），41=2×4×（4+1）+1
…观察以上各组勾股数组成特点，第7组勾股数是（只填数，不填等式）
三、解答题
-
16. 计算(1)、（2015﹣π）0+| ﹣2|+ +（ ）﹣1；(2)、先化简，再求值：（a﹣ ）（a+ ）﹣a（a﹣6），其中a= + ．17. 如图，菱形的对角线BD，AC的长分别是6和8，求菱形的周长与面积．
18. 如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．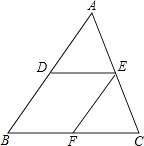
(1)、求证：四边形DBFE是平行四边形；(2)、当△ABC满足什么条件时，四边形DBFE是菱形？为什么？19. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
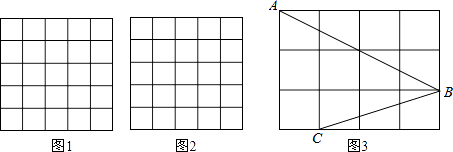(1)、在图1中以格点为顶点画一个面积为10的正方形；(2)、在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 ， ；(3)、如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．20. 如图，在矩形ABCD中，E为BC上一点，AE⊥DE，∠DAE=30°，若DE=m+n，且m、n满足m= + +2，试求BE的长．
21. 已知三角形三边之长能求出三角形的面积吗？海伦公式告诉你计算的方法是：S= ，其中S表示三角形的面积，a，b，c分别表示三边之长，p表示周长之半，即p= ．
我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致，所有这个公式也叫“海伦﹣秦九韶公式”．
请你利用公式解答下列问题．
(1)、在△ABC中，已知AB=5，BC=6，CA=7，求△ABC的面积；(2)、计算（1）中△ABC的BC边上的高．22. 如图，在△ABC中，点O是边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交△BCA的外角平分线于点F．
(1)、探究OE与OF的数量关系并加以证明；(2)、当点O在边AC运动时，四边形BCFE会是菱形吗？若是，请加以证明；若不是，则说明理由．(3)、当点O在AC运动到什么位置，四边形AECF是矩形，请说明理由；(4)、在（3）问的基础上，△ABC满足什么条件时，四边形AECF是正方形？为什么？