2015-2016学年山东省德州市夏津三中八年级下学期期中数学试卷
试卷更新日期:2016-10-13 类型:期中考试
一、选择题
-
1. 一次函数的图象经过点A(﹣2,﹣1),且与直线y=2x﹣3平行,则此函数的解析式为( )A、y=x+1 B、y=2x+3 C、y=2x﹣1 D、y=﹣2x﹣52. 永州市内货摩(运货的摩托)的运输价格为:2千米内运费5元;路程超过2千米的,每超过1千米增加运费1元,那么运费y元与运输路程x千米的函数图象是( )A、
 B、
B、 C、
C、 D、
D、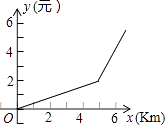 3.
3.已知一次函数y=kx+b的图象如图,则k、b的符号是( )
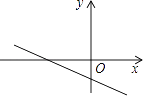 A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<04. 汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的函数关系用图象表示应为( )A、
A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<04. 汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的函数关系用图象表示应为( )A、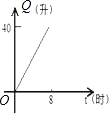 B、
B、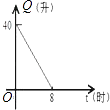 C、
C、 D、
D、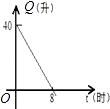 5. 若一次函数y=(1﹣2m)x+m的图象经过点A(x1 , y1)和点B(x2 , y2),当x1<x2时,y1<y2 , 且与y轴相交于正半轴,则 m的取值范围是( )A、m>0 B、m< C、0<m< D、m>6. 已知一次函数y=mx+|m+1|的图象与y轴交于点(0,3),且y随x的增大而增大,则m的值为( )A、2 B、﹣4 C、﹣2或﹣4 D、2或﹣47. 一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶.过了一段时间,汽车到达下一车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下图中近似地刻画出汽车在这段时间内的速度变化情况的是( )A、
5. 若一次函数y=(1﹣2m)x+m的图象经过点A(x1 , y1)和点B(x2 , y2),当x1<x2时,y1<y2 , 且与y轴相交于正半轴,则 m的取值范围是( )A、m>0 B、m< C、0<m< D、m>6. 已知一次函数y=mx+|m+1|的图象与y轴交于点(0,3),且y随x的增大而增大,则m的值为( )A、2 B、﹣4 C、﹣2或﹣4 D、2或﹣47. 一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶.过了一段时间,汽车到达下一车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下图中近似地刻画出汽车在这段时间内的速度变化情况的是( )A、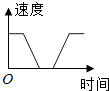 B、
B、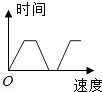 C、
C、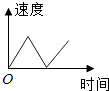 D、
D、 8. 直线y= x﹣6与直线y=﹣ x﹣ 的交点坐标是( )A、(﹣8,﹣10) B、(0,﹣6) C、(10,﹣1) D、以上答案均不对9. 下列函数中,y随x的增大而减小的有( )
8. 直线y= x﹣6与直线y=﹣ x﹣ 的交点坐标是( )A、(﹣8,﹣10) B、(0,﹣6) C、(10,﹣1) D、以上答案均不对9. 下列函数中,y随x的增大而减小的有( )①y=﹣2x+1;②y=6﹣x;③y= ;④y=(1﹣ )x.
A、1个 B、2个 C、3个 D、4个10. 一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )A、 B、
B、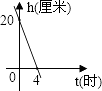 C、
C、 D、
D、
二、填空题
-
11. 直线y=3x+b与y轴的交点的纵坐标为﹣2,则这条直线一定不过象限.12. 一次函数y=(m2﹣4)x+(1﹣m)和y=(m﹣1)x+m2﹣3的图象与y轴分别交于点P和点Q,若点P与点Q关于x轴对称,则m= .13. 一次函数y=﹣2x+4的图象与x轴交点坐标是 , 与y轴交点坐标是 , 图象与坐标轴所围成的三角形面积是 .14. 已知关系x,y的二元一次方程3ax+2by=0和5ax﹣3by=19化成的两个一次函数的图象的交点坐标为(1,﹣1),则a= , b= .15. 若一次函数y=kx+b的函数值y随x的增大而减小,且图象与y轴的负半轴相交,那么对k和b的取值范围分别是和 .16. 已知函数 是一次函数,则m= , 此函数图象经过第象限.
三、解答题
-
17. 已知一次函数y=(2m+4)x+(3﹣n),求:(1)、当m是什么数时,y随x的增大而增大?(2)、当n为何值时,函数图象与y轴的交点在x轴下方?(3)、m,n为何值时,函数图象过原点?18. 已知y﹣2与x+1成正比例函数关系,且x=﹣2时,y=6.(1)、写出y与x之间的函数关系式;(2)、求当x=﹣3时,y的值;(3)、求当y=4时,x的值.19. 已知函数y=(m+1)x+2m﹣6,(1)、若函数图象过(﹣1,2),求此函数的解析式.(2)、若函数图象与直线y=2x+5平行,求其函数的解析式.(3)、求满足(2)条件的直线与直线y=﹣3x+1的交点,并求出这两条直线与y轴所围成三角形的面积.20. 如图,直线L: 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
 (1)、求A、B两点的坐标;(2)、求△COM的面积S与M的移动时间t之间的函数关系式;(3)、当t为何值时△COM≌△AOB,并求此时M点的坐标.21. 已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.(1)、求y(元)与x(套)的函数关系式,并求出自变量的取值范围;(2)、当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?22. 小刚家装修,准备安装照明灯.他和爸爸到市场进行调查,了解到某种优质品牌的一盏40瓦白炽灯的售价为1.5元,一盏8瓦节能灯的售价为22.38元,这两种功率的灯发光效果相当.假定电价为0.45元/度,设照明时间为x(小时),使用一盏白炽灯和一盏节能灯的费用分别为y1(元)和y2(元)[耗电量(度)=功率(千瓦)×用电时间(小时),费用=电费+灯的售价].(1)、分别求出y1、y2与照明时间x之间的函数表达式;(2)、你认为选择哪种照明灯合算?(3)、若一盏白炽灯的使用寿命为2000小时,一盏节能灯的使用寿命为6000小时,如果不考虑其他因素,以6000小时计算,使用哪种照明灯省钱?省多少钱?
(1)、求A、B两点的坐标;(2)、求△COM的面积S与M的移动时间t之间的函数关系式;(3)、当t为何值时△COM≌△AOB,并求此时M点的坐标.21. 已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.(1)、求y(元)与x(套)的函数关系式,并求出自变量的取值范围;(2)、当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?22. 小刚家装修,准备安装照明灯.他和爸爸到市场进行调查,了解到某种优质品牌的一盏40瓦白炽灯的售价为1.5元,一盏8瓦节能灯的售价为22.38元,这两种功率的灯发光效果相当.假定电价为0.45元/度,设照明时间为x(小时),使用一盏白炽灯和一盏节能灯的费用分别为y1(元)和y2(元)[耗电量(度)=功率(千瓦)×用电时间(小时),费用=电费+灯的售价].(1)、分别求出y1、y2与照明时间x之间的函数表达式;(2)、你认为选择哪种照明灯合算?(3)、若一盏白炽灯的使用寿命为2000小时,一盏节能灯的使用寿命为6000小时,如果不考虑其他因素,以6000小时计算,使用哪种照明灯省钱?省多少钱?