2015-2016学年江西省宜春市高安市八年级下学期期中数学试卷
试卷更新日期：2016-10-13 类型：期中考试
一、选择题：
-
1. 下列二次根式中，属于最简二次根式的是（ ）A、 B、 C、 D、2. 以下各组数为边长的三角形中，能组成直角三角形的是（ ）A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，63. 已知：如图，菱形ABCD中，对角线AC与BD相交于点O，OE∥AB交BC于点E，AD=6cm，则OE的长为（ ）
A、6cm B、4cm C、3cm D、2cm4. 若顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是（ ）A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形5. 如图，以正方形ABCD的对角线AC为一边作菱形AEFC，则∠FAB=（ ）
A、30° B、45° C、22.5° D、135°6. 如图，在5×5的正方形网格中，以AB为边画直角△ABC，使点C在格点上，满足这样条件的点C的个数（ ）
A、6 B、7 C、8 D、9二、填空题：
-
7. 已知函数y= ，则自变量x的取值范围是 ．8. 已知 ，则x3y+xy3= ．9. 如图，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E、F，AB=2，BC=3，则图中阴影部分的面积为 ．
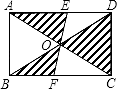10. 如图，若▱ABCD的周长为36cm，过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，▱ABCD的面积为 cm2 ．
11. 已知Rt△ABC中，∠C=90°，a+b=14cm，c=10cm，则Rt△ABC的面积等于 ．12. 如图，圆柱形容器中，高为1.2m，底面周长为1m，在容器内壁离容器底部0.3m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为 m（容器厚度忽略不计）．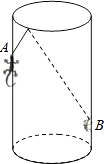
13. 如图，矩形纸片ABCD中，AB=6cm，AD=10cm，点E、F在矩形ABCD的边AB、AD上运动，将△AEF沿EF折叠，使点A′在BC边上，当折痕EF移动时，点A′在BC边上也随之移动．则A′C的取值范围为 ．
14. 如图，在△ABC中，AB=AC=5，P是BC边上除点B、C外的任意一点，则AP2+PB•PC= ．
三、解答
-
15. 计算：（π﹣1）0+ + ﹣2 ．16. 先化简，再求值： ，其中x= ．17. 在如图所示的5×5的正方形网格中，每个小正方形的边长均为1，按下列要求画图或填空；
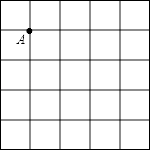(1)、画一条线段AB使它的另一端点B落在格点上（即小正方形的顶点），且AB=2 ；(2)、以（1）中的AB为边画一个等腰△ABC，使点C落在格点上，且另两边的长都是无理数；(3)、△ABC的周长为 ， 面积为 ．18. 已知实数a、b、c在数轴上的位置如图所示，化简： ﹣|a+b|+ +|b﹣c|
四、解答题
-
19. 如图所示，在菱形ABCD中，∠BAD=120°，AB=4．求：
(1)、对角线AC，BD的长；(2)、菱形ABCD的面积．20. 已知a，b，c是△ABC的三边，且a2+b2+c2﹣12a﹣16b﹣20c+200=0，试判断△ABC的形状．21. 如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．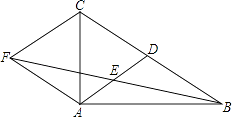
(1)、求证：AF=DC；(2)、若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．22. 如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G．
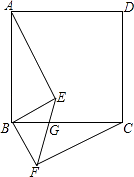(1)、求证：AE=CF；(2)、若∠ABE=55°，求∠EGC的大小．五、解答题
-
23. 图①是一面矩形彩旗完全展平时的尺寸图（单位：cm），其中矩形ABCD是由双层白布缝制的穿旗杆用的旗裤，阴影部分DCEF为矩形绸缎旗面．
(1)、用经加工的圆木杆穿入旗裤作旗杆，求旗杆的最大直径（精确到1cm）；(2)、将穿好彩旗的旗杆垂直插在操场上，旗杆从旗顶到地面的高度为220cm，在无风的天气里，彩旗自然下垂，如图②，求彩旗下垂时最低处离地面的最小高度h．六、解答题
-
24. 正方形ABCD中，点O是对角线DB的中点，点P是DB所在直线上的一个动点，PE⊥BC于E，PF⊥DC于F．
(1)、当点P与点O重合时（如图①），猜测AP与EF的数量及位置关系，并证明你的结论；(2)、当点P在线段DB上（不与点D、O、B重合）时（如图②），探究（1）中的结论是否成立？若成立，写出证明过程；若不成立，请说明理由；(3)、当点P在DB的长延长线上时，请将图③补充完整，并判断（1）中的结论是否成立？若成立，直接写出结论；若不成立，请写出相应的结论．
-