2015-2016学年湖北省宜昌三中八年级下学期期中数学试卷
试卷更新日期:2016-10-13 类型:期中考试
一、选择题
-
1. 式子 在实数范围内有意义,则x的取值范围是( )A、x>1 B、x≥1 C、x<1 D、x≤12. 下列各点,不在函数y=2x﹣1的图象上的是( )A、(2,3) B、(﹣2,﹣5) C、(0,﹣1) D、(﹣1,0)3. 下列运算正确的是( )A、× =3 B、÷ =4 C、3+ =3 D、+ =4. 下列三条线段不能构成直角三角形的是( )A、1、 、2 B、、 、 C、5、12、13 D、9、40、415. 已知点(﹣4,y1),(2,y2)都在直线y=﹣ x+2上,则y1 , y2大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能比较6. 在下列性质中,平行四边形不一定具有的是( )A、对边相等 B、对边平行 C、对角互补 D、内角和为360°7. 菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为( )A、3:1 B、4:1 C、5:1 D、6:18. 在△ABC中,AB=1,AC= ,BC=2,则这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形9. 如图.在菱形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
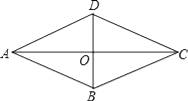 A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OC10. 如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是( )
A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OC10. 如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是( ) A、
A、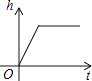 B、
B、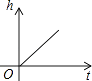 C、
C、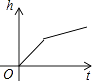 D、
D、 11. 在下列命题中,正确的是( )A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形12. 已知一次函数y=kx+b的图象经过一、二、四象限,则直线y=bx﹣k的图象可能是( )A、
11. 在下列命题中,正确的是( )A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形12. 已知一次函数y=kx+b的图象经过一、二、四象限,则直线y=bx﹣k的图象可能是( )A、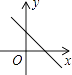 B、
B、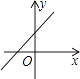 C、
C、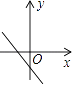 D、
D、 13. 如图,矩形ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AC=8,AB的长度是( )
13. 如图,矩形ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AC=8,AB的长度是( )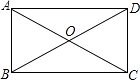 A、4 B、4 C、4 D、814. 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以OB为半径画圆,交数轴于点C,则OC的长为( )
A、4 B、4 C、4 D、814. 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以OB为半径画圆,交数轴于点C,则OC的长为( )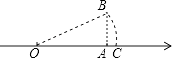 A、3 B、 C、 D、15. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
A、3 B、 C、 D、15. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )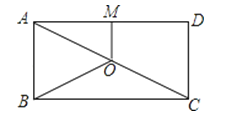 A、17 B、18 C、19 D、20
A、17 B、18 C、19 D、20二、解答题
-
16. 计算: ( ﹣ )+( +1)2 .17. 求如图的Rt△ABC的面积.
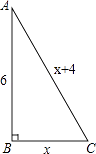 18. 一次函数图象经过(3,8)和(5,12)两点,求一次函数解析式.19. 某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系式如图所示.
18. 一次函数图象经过(3,8)和(5,12)两点,求一次函数解析式.19. 某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系式如图所示.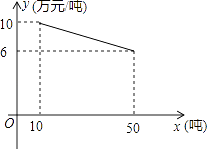 (1)、求y关于x的函数解析式,并写出自变量的取值范围;(2)、当每吨成本为9万元时,求该产品的生产数量.20. 正方形ABCD中,AB=4,对角线交于点O,F是BO的中点,连接AF,求AF的长度.
(1)、求y关于x的函数解析式,并写出自变量的取值范围;(2)、当每吨成本为9万元时,求该产品的生产数量.20. 正方形ABCD中,AB=4,对角线交于点O,F是BO的中点,连接AF,求AF的长度.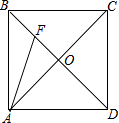 21. 如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.
21. 如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.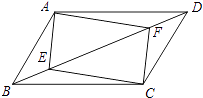 (1)、若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;(2)、若四边形AECF是菱形,则四边形ABCD是菱形吗?请说明理由?(3)、若四边形AECF是矩形,则四边形ABCD是矩形吗?不必写出理由.22. 某欢乐谷为回馈广大谷迷,在暑假期间推出学生个人门票优惠价,各票价如下:
(1)、若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;(2)、若四边形AECF是菱形,则四边形ABCD是菱形吗?请说明理由?(3)、若四边形AECF是矩形,则四边形ABCD是矩形吗?不必写出理由.22. 某欢乐谷为回馈广大谷迷,在暑假期间推出学生个人门票优惠价,各票价如下:票价种类
(A)学生夜场票
(B)学生日通票
(C)节假日通票
单价(元)
80
120
150
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生,其中购买的B种票数是A种票数的3倍还多7张,设购买A种票x张,C种票y张.
(1)、直接写出x与y之间的函数关系式;(2)、设购票总费用为W元,求W(元)与x(张)之间的函数关系式;(3)、为方便学生游玩,计划购买的学生夜场票不低于20张,且每种票至少购买5张,则有几种购票方案?并指出哪种方案费用最少.23.如图,在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD的内部,延长AF交CD于点G.
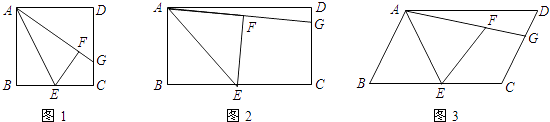 (1)、猜想并证明线段GF与GC的数量关系;(2)、若将图1中的正方形改成矩形,其它条件不变,如图2,那么线段GF与GC之间的数量关系是否改变?请证明你的结论;(3)、若将图1中的正方形改成平行四边形,其它条件不变,如图3,那么线段GF与GC之间的数量关系是否会改变?请证明你的结论.24. 如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.
(1)、猜想并证明线段GF与GC的数量关系;(2)、若将图1中的正方形改成矩形,其它条件不变,如图2,那么线段GF与GC之间的数量关系是否改变?请证明你的结论;(3)、若将图1中的正方形改成平行四边形,其它条件不变,如图3,那么线段GF与GC之间的数量关系是否会改变?请证明你的结论.24. 如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.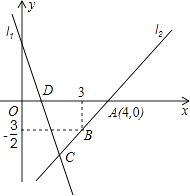 (1)、求直线l2的解析表达式;(2)、求△ADC的面积;(3)、若点P为第一象限上的一点,且以A,C,D,P为顶点的四边形为平行四边形,试求点P的坐标.
(1)、求直线l2的解析表达式;(2)、求△ADC的面积;(3)、若点P为第一象限上的一点,且以A,C,D,P为顶点的四边形为平行四边形,试求点P的坐标.