河北省邢台市2016-2017学年高二下学期理数期末考试试卷

试卷更新日期：2017-12-15 类型：期末考试

进入出卷网下载

一、选择题

1. 已知复数z满足zi⁵=1+2i，则 $\bar{z}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 两个变量y与x的回归模型中，分别选择了4个不同模型，它们对应的R²=1﹣ $\frac{\sum_{i = 1}^{n} {(y_{i} - \hat{y_{i}})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}$ 的值如下，其中拟合效果最好的模型是（）

A、模型1对应的R²=0.48 B、模型3对应的R²=0.15 C、模型2对应的R²=0.96 D、模型4对应的R²=0.30

查看试题解析
3. 用数学归纳法证明“凸n变形对角线的条数f（n）= $\frac{n (n - 3)}{2}$ ”时，第一步应验证（）

A、n=1成立 B、n=2成立 C、n=3成立 D、n=4成立

查看试题解析
4. 下列曲线中，在x=1处切线的倾斜角为 $\frac{3 π}{4}$ 的是（）

A、y=x²﹣ $\frac{3}{x}$ B、y=xlnx C、y=sin（πx） D、y=x³﹣2x²

查看试题解析
5. 已知随机变量X服从正态分布N（100，4），若P（102＜X＜m）=0.1359，则m等于[驸：P（μ﹣σ＜X＜μ+σ）=0.6826，P（μ﹣2σ＜X＜μ+2σ）=0.9544]（）

A、103 B、104 C、105 D、106

查看试题解析
6. 把3名新生分到甲、乙、丙、丁四个班，每个班至多分配1名且甲班必须分配1名，则不同的分配方法有（）

A、12种 B、15种 C、18种 D、20种

查看试题解析
7. 给出下面三个类比结论：
①向量 $\vec{a}$ ，有| $\vec{a}$ |²= $\vec{a}$ ²；类比复数z，有|z|²=z²
②实数a，b有（a+b）²=a²+2ab+b²；类比向量 $\vec{a}$ ， $\vec{b}$ ，有（ $\vec{a} + \vec{b}$ ）²= $\vec{a}$ ² $+ 2 \vec{a} \cdot \vec{b} + \vec{b}$ ²
③实数a，b有a²+b²=0，则a=b=0；类比复数z₁ ， z₂ ，有z₁²+z₂²=0，则z₁=z₂=0
其中类比结论正确的命题个数为（）

A、0 B、1 C、2 D、3

查看试题解析
8. ${(3 \sqrt{x} - 2 \sqrt[3]{x})}^{11}$ 展开式中任取一项，则所取项是有理项的概率为（）

A、 $\frac{1}{12}$ B、 $\frac{1}{6}$ C、 $\frac{2}{11}$ D、 $\frac{1}{11}$

查看试题解析
9. 袋中有6个黄色、4个白色的乒乓球，做不放回抽样，每次任取1个球，取2次，则关于事件“直到第二次才取到黄色球”与事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率说法正确的是（）

A、事件“直到第二次才取到黄色球”与事件“第一次取到白球的情况下，第二次恰好取得黄球”的概率都等于 $\frac{2}{3}$ B、事件“直到第二次才取到黄色球”与事件“第一次取到白球的情况下，第二次恰好取得黄球”的概率都等于 $\frac{4}{15}$ C、事件“直到第二次才取到黄色球”的概率等于 $\frac{2}{3}$ ，事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率等于 $\frac{4}{15}$ D、事件“直到第二次才取到黄色球”的概率等于 $\frac{4}{15}$ ，事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率等于 $\frac{2}{3}$

查看试题解析
10. 已知f（x）= $\frac{2 x}{2 - x}$ ，设f₁（x）=f（x），f_n（x）=f_n_﹣1[f_n_﹣1（x）]（n＞1，n∈N*），若f_m（x）= $\frac{x}{1 - 256 x}$ （m∈N*），则m等于（）

A、9 B、10 C、11 D、126

查看试题解析
11. 3男3女共6名同学从左至右排成一排合影，要求左端排男同学，右端排女同学，且女同学至多有2人排在一起，则不同的排法种数为（）

A、144 B、160 C、180 D、240

查看试题解析
12. 已知函数f（x）=﹣ $\frac{2 + a x^{2}}{e^{x}}$ （a＞0）在区间[0，1]上有极值，且函数f（x）在区间[0，1]上的最小值不小于﹣ $\frac{7}{e}$ ，则a的取值范围是（）

A、（2，5] B、（2，+∞） C、（1，4} D、[5，+∞）

查看试题解析

二、填空题

13. 若（2x²﹣3）ⁿ展开式中第3项的二项式系数为15，则n= ．

查看试题解析
14. 曲线f（x）=sin（ $\frac{π}{6}$ ﹣x）与直线x=﹣ $\frac{π}{6}$ ，x= $\frac{π}{6}$ ，y=0所围成的平面图形的面积为．

查看试题解析
15. 已知复数z=（2a+i）（1﹣bi）的实部为2，其中a，b为正实数，则4^a+（ $\frac{1}{2}$ ）^1﹣b的最小值为．

查看试题解析
16. 某校组织“中国诗词”竞赛，在“风险答题”的环节中，共为选手准备了A、B、C三类不同的题目，选手每答对一个A类、B类或C类的题目，将分别得到300分、200分、100分，但如果答错，则相应要扣去300分、200分、100分，根据平时训练经验，选手甲答对A类、B类或C类题目的概率分别为0.6、0.75、0.85，若腰每一次答题的均分更大一些，则选手甲应选择的题目类型应为（填A、B或C）

查看试题解析

三、解答题

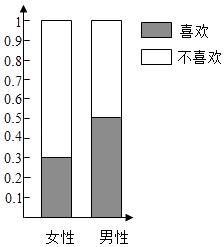
17. 为了调查喜欢旅游是否与性别有关，调查人员就“是否喜欢旅游”这个问题，在火车站分别随机调研了50名女性和50名男性，根据调研结果得到如图所示的等高条形图
（Ⅰ）完成下列2×2列联表：

喜欢旅游
不喜欢旅游
合计
女性

男性

合计

（II）能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关”
附：
P（K²≥k₀）
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k₀
2.072
2.706
3.841
5.024
6.635
7.879
10.828
（参考公式：K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d）

查看试题解析
18. 国内某汽车品牌一个月内被消费者投诉的次数用X表示，据统计，随机变量X的概率分布如下：
X
0
1
2
3
P
0.1
0.3
2a
a

(1)、求a的值；

(2)、假设一月份与二月份被消费者投诉的次数互不影响，求该汽车品牌在这两个月内共被消费者投诉2次的概率．

查看试题解析
19. 已知函数f（x）=x³+ax²+bx+a²（a、b∈R）

(1)、若函数f（x）在x=1处有极值为10，求b的值；

(2)、若a=﹣4，f（x）在x∈[0，2]上单调递增，求b的最小值．

查看试题解析
20. 已知a＞0，b＞0．

(1)、求证： $\frac{1}{a}$ + $\frac{2}{b}$ ≥ $\frac{8}{2 a + b}$ ；

(2)、若c＞0，求证：在a﹣b﹣c，b﹣a﹣c，c﹣a﹣b中至少有两个负数．

查看试题解析
21. 中学阶段是学生身体发育最重要的阶段，长时间熬夜学习严重影响学生的身体健康，某校为了解甲、乙两班每周自我熬夜学习的总时长（单位：小时），分别从这两个班中随机抽取6名同学进步调查，将他们最近一周自我熬夜学习的总时长作为样本数据，绘制成茎叶图如图所示（图中的茎表示十位数字，叶表示个位数字）．如果学生平均每周
自我熬夜学习的总时长超过21小时，则称为“过度熬夜”．
（Ⅰ）请根据样本数据，分别估计甲，乙两班的学生平均每周自我熬夜学习时长的平均值；
（Ⅱ）从甲班的样本数据中有放回地抽取2个数据，求恰有1个数据为“过度熬夜”的概率；
（Ⅲ）从甲班、乙班的样本中各随机抽取2名学生的数据，记“过度熬夜”的学生人数为X，写出X的分布列和数学期望E（X）．

查看试题解析
22. 已知函数f（x）=（2x+b）e^x ， F（x）=bx﹣lnx，b∈R．

(1)、若b＜0，且存在区间M，使f（x）和F（x）在区间M上具有相同的单调性，求b的取值范围；

(2)、若F（x+1）＞b对任意x∈（0，+∞）恒成立，求b的取值范围．

查看试题解析

P（K²≥k₀）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.072	2.706	3.841	5.024	6.635	7.879	10.828

	喜欢旅游	不喜欢旅游	合计
女性
男性
合计

X	0	1	2	3
P	0.1	0.3	2a	a