2015-2016学年山东省临沂市兰陵四中高一下学期期中数学试卷

试卷更新日期：2016-10-12 类型：期中考试

进入出卷网下载

一、选择题

1. 与角﹣ $\frac{π}{3}$ 终边相同的角是（）

A、 $\frac{2 π}{3}$ B、 $\frac{π}{6}$ C、 $\frac{5 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
2. 已知平面向量 $\vec{a}$ =（1，2）， $\vec{b}$ =（1，﹣1），则向量 $\frac{1}{3}$ $\vec{a}$ ﹣ $\frac{4}{3}$ $\vec{b}$ =（）

A、（﹣2，﹣1） B、（﹣2，1） C、（﹣1，0） D、（﹣1，2）

查看试题解析
3. 下列函数中，周期为π的是（）

A、y=cos4x B、y=tan2x C、y=sin2x D、 $y = \sin \frac{x}{2}$

查看试题解析
4. 圆的方程是（x﹣1）（x+2）+（y﹣2）（y+4）=0，则圆心的坐标是（）

A、（1，﹣1） B、（ $\frac{1}{2}$ ，﹣1） C、（﹣1，2） D、（﹣ $\frac{1}{2}$ ，﹣1）

查看试题解析
5. 若sinα=﹣ $\frac{5}{13}$ ，则α为第四象限角，则tanα的值等于（）

A、 $\frac{12}{5}$ B、﹣ $\frac{12}{5}$ C、 $\frac{5}{12}$ D、﹣ $\frac{5}{12}$

查看试题解析
6. 已知函数f（x）= $\sqrt{2}$ sin（2x﹣ $\frac{π}{6}$ ），当x∈[0， $\frac{π}{2}$ ]时，f（x）的最大值、最小值分别为（）

A、 $\sqrt{2}$ 、﹣ $\frac{\sqrt{2}}{2}$ B、1、﹣ $\frac{1}{2}$ C、1、﹣ $\frac{\sqrt{2}}{2}$ D、 $\sqrt{2}$ 、 $\frac{\sqrt{2}}{2}$

查看试题解析
7. 已知| $\vec{a}$ |=2，| $\vec{b}$ |=3，| $\vec{a}$ + $\vec{b}$ |= $\sqrt{19}$ ，则| $\vec{a}$ ﹣ $\vec{b}$ |等于（）

A、 $\sqrt{13}$ B、 $\sqrt{15}$ C、 $\sqrt{17}$ D、 $\sqrt{7}$

查看试题解析
8. 若圆x²+y²=r²和（x﹣3）²+（y+1）²=r²外切，则正实数r的值是（）

A、 $\sqrt{10}$ B、 $\frac{\sqrt{10}}{2}$ C、 $\sqrt{5}$ D、5

查看试题解析
9. 设P是△ABC所在平面内的一点， $\vec{B C} + \vec{B A} = 2 \vec{B P}$ ，则（）

A、 $\vec{P A} + \vec{P B} = \vec{0}$ B、 $\vec{P A} + \vec{P C} = \vec{0}$ C、 $\vec{P B} + \vec{P C} = \vec{0}$ D、 $\vec{P A} + \vec{P B} + \vec{P C} = \vec{0}$

查看试题解析
10. 一条光线从点（﹣2，﹣3）射出，经y轴反射后与圆（x+3）²+（y﹣2）²=1相切，则反射光线所在直线的斜率为（　　）

A、﹣ $\frac{5}{3}$ 或﹣ $\frac{3}{5}$ B、﹣ $\frac{3}{2}$ 或﹣ $\frac{2}{3}$ C、﹣ $\frac{5}{4}$ 或﹣ $\frac{4}{5}$ D、﹣ $\frac{4}{3}$ 或﹣ $\frac{3}{4}$

查看试题解析

二、填空题

11. 设 $\vec{e_{1}} ， \vec{e_{2}}$ 是两个不共线的向量，已知 $\vec{A B} = 2 \vec{e_{1}} + k \vec{e_{2}} ， \vec{B C} = \vec{e_{1}} - 3 \vec{e_{2}}$ 若A，B，C三点共线，则实数k的值是．

查看试题解析
12. 已知直线l：x﹣y+4=0与圆C：（x﹣1）²+（y﹣1）²=2，则C上各点到l的距离的最小值为．

查看试题解析
13. 已知角α的终边在函数y=﹣|x|的图象上，则cosα的值为．

查看试题解析
14. 已知向量 $\vec{a}$ =（1，1）， $\vec{b}$ =（2，﹣3），若 $k \vec{a} - 2 \vec{b}$ 与 $\vec{a}$ 垂直，则实数k等于．

查看试题解析
15. 给出下列四个命题：
①函数y=2sin（2x﹣ $\frac{π}{3}$ ）的一条对称轴是x= $\frac{5 π}{12}$ ；
②函数y=tanx的图象关于点（ $\frac{π}{2}$ ，0）对称；
③正弦函数在第一象限为增函数
④存在实数α，使 $\sqrt{2}$ sin（α+ $\frac{π}{4}$ ）= $\frac{3}{2}$
以上四个命题中正确的有（填写正确命题前面的序号）

查看试题解析

三、解答题

16. 已知角α终边上一点P（﹣4，3），求 $\frac{\cos (\frac{π}{2} + α) \sin (- π - α)}{\cos (\frac{11 π}{2} - α) \sin (\frac{9 π}{2} + α)}$ 的值．

查看试题解析
17. 已知向量| $\vec{a}$ |=2，| $\vec{b}$ |=1，（2 $\vec{a}$ ﹣3 $\vec{b}$ ）•（2 $\vec{a} + \vec{b}$ ）=9．

(1)、求向量 $\vec{a}$ 与向量 $\vec{b}$ 的夹角θ；

(2)、求向量 $\vec{a}$ 在 $\vec{a} + \vec{b}$ 方向上的投影．

查看试题解析
18. 已知直线l：x﹣my+3=0和圆C：x²+y²﹣6x+5=0

(1)、当直线l与圆C相切时，求实数m的值；

(2)、当直线l与圆C相交，且所得弦长为 $\frac{2 \sqrt{10}}{5}$ 时，求实数m的值．

查看试题解析
19. 已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜ $\frac{π}{2}$ ）的部分图象如图．

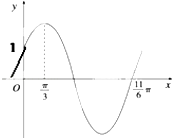(1)、求f（x）的解析式；

(2)、将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的 $\frac{1}{2}$ 倍，再将所得函数图象向右平移 $\frac{π}{6}$ 个单位，得到函数y=g（x）的图象，求g（x）的单调递增区间．

查看试题解析
20. 已知过点A（0，1）且斜率为k的直线l与圆C：（x﹣2）²+（y﹣3）²=1交于点M、N两点．

(1)、求k的取值范围；

(2)、若 $\vec{O M}$ • $\vec{O N}$ =12，其中O为坐标原点，求|MN|．

查看试题解析
21. 设函数f（x）=2sin（2x+φ）（0＜φ＜π），y=f（x）图象的一个对称中心是 $(\frac{π}{3} ， 0)$ ．

(1)、求φ；

(2)、在给定的平面直角坐标系中作出该函数在x∈[0，π]的图象；

(3)、求函数f（x）≥1（x∈R）的解集．

查看试题解析