2015-2016学年河南省郑州106中高一下学期期中数学试卷

试卷更新日期：2016-10-12 类型：期中考试

进入出卷网下载

一、选择题

1. 如果输入n=3，那么执行如图中算法的结果是（）

A、输出3 B、输出4 C、输出5 D、程序出错，输不出任何结果

查看试题解析
2. 下列说法中正确的是（）

A、数据4、6、6、7、9、4的众数是4 B、一组数据的标准差是这组数据的方差的平方 C、数据3，5，7，9的标准差是数据6、10、14、18的标准差的一半 D、频率分布直方图中各小长方形的面积等于相应各组的频数

查看试题解析
3. 某初级中学领导采用系统抽样方法，从该校预备年级全体800名学生中抽50名学生．现将800名学生从1到800进行编号，如果抽到的是7，则从33～48这16个数中应取的数是（）

A、40 B、39 C、38 D、37

查看试题解析
4. 从1，2，3，4这4个数中，不放回地任意取两个数，两个数都是奇数的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
5. 把11化为二进制数为（　　）

A、1 011_（2） B、11 011_（2） C、10 110_（2） D、0 110_（2）

查看试题解析
6. 若扇形圆心角的弧度数为2，且扇形弧所对的弦长也是2，则这个扇形的面积为（）

A、 $\frac{1}{\sin^{2} 1}$ B、 $\frac{2}{\sin^{2} 2}$ C、 $\frac{1}{\cos^{2} 1}$ D、 $\frac{2}{\cos^{2} 2}$

查看试题解析
7. 若α的终边过点P（2sin30°，﹣2cos30°），则sinα的值为（）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、﹣ $\frac{\sqrt{3}}{2}$ D、﹣ $\frac{\sqrt{3}}{3}$

查看试题解析
8. 执行图的程序，如果输出的结果是4，那么输入的只可能是（）

A、﹣2或2 B、2 C、﹣2或4 D、2或﹣4

查看试题解析
9. 按照程序框图（如图）执行，第3个输出的数是（）

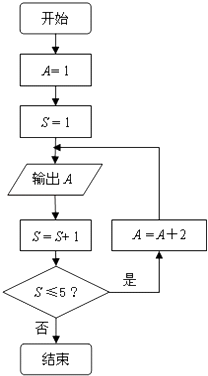A、3 B、4 C、5 D、6

查看试题解析
10. 设cos（α+π）= $\frac{\sqrt{3}}{2}$ （π＜α＜ $\frac{3 π}{2}$ ），那么sin（2π﹣α）的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、﹣ $\frac{\sqrt{3}}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
11. 已知sinα是方程5x²﹣7x﹣6=0的根，且α是第三象限角，则 $\frac{\sin (- α - \frac{3 π}{2}) \cos (\frac{3 π}{2} - α) \tan^{2} (π - α)}{\cos (\frac{π}{2} - α) \sin (\frac{π}{2} + α)}$ =（）

A、 $\frac{9}{16}$ B、﹣ $\frac{9}{16}$ C、 $\frac{3}{4}$ D、﹣ $\frac{3}{4}$

查看试题解析
12. 已知函数f（x）=asin（πx+α）+bcos（πx+β），且f（2 009）=3，则f（2 011）的值是（）

A、﹣1 B、﹣2 C、3 D、1

查看试题解析

二、填空题

13. 已知tanθ=2，则sin²θ+sinθcosθ﹣2cos²θ= ．

查看试题解析
14. 如图，在半径为R的圆内随机撒一粒黄豆，它落在阴影部分内接正三角形上的概率是

查看试题解析
15. 如图是某学校学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为10，则抽取的学生人数是．

查看试题解析
16. 若角α的终边落在直线y=﹣x上，则 $\frac{\sin α}{\sqrt{1 - s i n^{2} α}}$ + $\frac{\sqrt{1 - \cos^{2} α}}{\cos α}$ 的值等于．

查看试题解析

三、解答题

17. 已知cosα=﹣ $\frac{4}{5}$ ，求sinα，tanα

查看试题解析
18. 已知sin（π﹣α）﹣cos（π+α）= $\frac{\sqrt{2}}{3}$ （ $\frac{π}{2}$ ＜α＜π）．求：

(1)、sinα﹣cosα；

(2)、tanα+ $\frac{1}{\tan α}$ ．

查看试题解析
19. 某校从参加高三期中考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），数学成绩分组及样本频率分布表如下：
分组
频数
频率
[40，50）
2
0.04
[50，60）
3
0.06
[60，70）
14
0.28
[70，80）
15
②
[80，90）
①
0.24
[90，100]
4
0.08
合计
③
④

(1)、请把给出的样本频率分布表中的空格都填上；

(2)、为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩[90，100]中选两位同学，共同帮助[40，50）中的某一位同学，已知甲同学的成绩为42分，乙同学的成绩为95分，求甲、乙两同学恰好被安排在同一小组的概率．

查看试题解析
20. 为了了解小学生的体能情况，抽取了某校一个年级的部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），已知图中从左到右前三个小组的频率分别为 0.1，0.3，0.4，第一小组的频数为 5．

(1)、求第四小组的频率；

(2)、若次数在 75 次以上（含75 次）为达标，试估计该年级学生跳绳测试的达标率．

(3)、在这次测试中，一分钟跳绳次数的中位数落在哪个小组内？试求出中位数．

查看试题解析
21. 某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应：
X
2
4
5
6
8
y
30
40
60
50
70

(1)、求回归直线方程．

(2)、回归直线必经过的一点是哪一点？

查看试题解析
22. 若以连续掷两次骰子分别得到的点数m、n作为点P的坐标（m，n），求：

(1)、点P在直线x+y=7上的概率；

(2)、点P在圆x²+y²=25外的概率．

(3)、将m，n，5的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率．

查看试题解析

分组	频数	频率
[40，50）	2	0.04
[50，60）	3	0.06
[60，70）	14	0.28
[70，80）	15	②
[80，90）	①	0.24
[90，100]	4	0.08
合计	③	④