浙教版数学八年级上册跨学科素养培优专题测试
试卷更新日期:2025-11-27 类型:复习试卷
一、第1-6题每题3分,第7题7分,第8题6分,共31分
-
1. 《国语·楚语》有云:“夫美也者,上下、内外、大小、远近皆无害焉,故曰美。”里里外外皆均衡妥帖,方为“美”,对称即是这样的美。下列航空公司的标志是轴对称图形的是( )A、
 贵州航空
B、
贵州航空
B、 中国南方航空
C、
中国南方航空
C、 江西航空
D、
江西航空
D、 中国国际航空
2. 如图是脊柱侧弯的检测示意图,在体检时为方便测出角的大小,需将转化为与它相等的角,则图中与相等的角是( )
中国国际航空
2. 如图是脊柱侧弯的检测示意图,在体检时为方便测出角的大小,需将转化为与它相等的角,则图中与相等的角是( )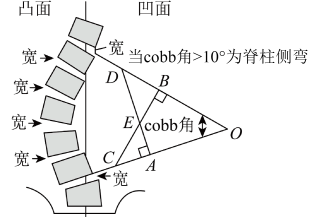 A、 B、 C、 D、3. 把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率P的函数图象(如图1),插线板电源线产生的热量Q与I的函数图象(如图2).下列结论中错误的是( )
A、 B、 C、 D、3. 把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I与使用电器的总功率P的函数图象(如图1),插线板电源线产生的热量Q与I的函数图象(如图2).下列结论中错误的是( ) A、当P=440W时,I=2A B、Q随I的增大而增大 C、I每增加1A,Q的增加量相同 D、P越大,插线板电源线产生的热量Q越多4. 花江峡谷大桥的主体钢结构中广泛应用了三角形框架,其核心原理是 , 这一特性使其能有效抵抗外力形变,保障桥梁稳固.
A、当P=440W时,I=2A B、Q随I的增大而增大 C、I每增加1A,Q的增加量相同 D、P越大,插线板电源线产生的热量Q越多4. 花江峡谷大桥的主体钢结构中广泛应用了三角形框架,其核心原理是 , 这一特性使其能有效抵抗外力形变,保障桥梁稳固. 5. 进行心肺复苏急救措施时,一般胸外心脏按压速度x(单位:次)的范围如图所示,则x的取值范围可表示为 .
5. 进行心肺复苏急救措施时,一般胸外心脏按压速度x(单位:次)的范围如图所示,则x的取值范围可表示为 . 6. 山西风景秀丽,历史文化悠久,自古以来众多文人墨客写下了很多赞美山西或以山西为背景的诗句,李贺的《雁门太守行》便是其中传诵千古的著名诗篇,将这首诗放入下图直角坐标系内,如甲的对应坐标为(1,2),请回答下方问题:
6. 山西风景秀丽,历史文化悠久,自古以来众多文人墨客写下了很多赞美山西或以山西为背景的诗句,李贺的《雁门太守行》便是其中传诵千古的著名诗篇,将这首诗放入下图直角坐标系内,如甲的对应坐标为(1,2),请回答下方问题: (1)、“云”、“塞”和“龙”的坐标依次是、和 .(2)、请直接写出(-4,-2),(-3,1),(4,-1)依次对应的文字.(3)、若将平面直角坐标系向右平移3个单位,向上平移1个单位,诗句不动.则坐标系平移后“鼓”字的新坐标为 .7. 植物呼吸作用受温度影响很大,观察如图,回答问题.
(1)、“云”、“塞”和“龙”的坐标依次是、和 .(2)、请直接写出(-4,-2),(-3,1),(4,-1)依次对应的文字.(3)、若将平面直角坐标系向右平移3个单位,向上平移1个单位,诗句不动.则坐标系平移后“鼓”字的新坐标为 .7. 植物呼吸作用受温度影响很大,观察如图,回答问题. (1)、此图反映的自变量和因变量分别是什么?(2)、温度在什么范围内时豌豆苗的呼吸强度逐渐变强? 在什么范围内逐渐减弱?(3)、要使豌豆呼吸作用最强,应控制在什么温度左右? 要抑制豌豆的呼吸应控制在什么温度左右?
(1)、此图反映的自变量和因变量分别是什么?(2)、温度在什么范围内时豌豆苗的呼吸强度逐渐变强? 在什么范围内逐渐减弱?(3)、要使豌豆呼吸作用最强,应控制在什么温度左右? 要抑制豌豆的呼吸应控制在什么温度左右?二、第11-17题每题3分,第18题6分,第19-20题每题8分,第21题8分,共57分.
-
8. 篮球比赛积分规则是胜一场得2分,负一场得1分.2025年某篮球联赛中,太阳队与月亮队要争夺出线权,太阳队当时的战绩是17胜13负,后面还有6场比赛;月亮队当时的战绩是15胜16负,后面还有5场比赛.为了确保出线,太阳队在后面的比赛中至少要胜多少场? ( )A、3 B、4 C、5 D、69. 如图,点A 在观测点北偏东30°方向,且与观测点之间的距离为8千米,将点A 的位置记作A(8,30°).用同样的方法将点B,点 C 的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )
 A、点O1处 B、点O2处 C、点O3处 D、点O4处10. 如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( )
A、点O1处 B、点O2处 C、点O3处 D、点O4处10. 如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数y(单位:N)与铁块被提起的时间x(单位:s)之间的函数关系的大致图象是( ) A、
A、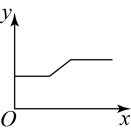 B、
B、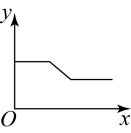 C、
C、 D、
D、 11. “儿子学成今日返,儿子已到父未到,父亲到后细端详,父子高兴把家还,”如图,用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下列图象与上述诗的含义大致相吻合的是( )A、
11. “儿子学成今日返,儿子已到父未到,父亲到后细端详,父子高兴把家还,”如图,用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下列图象与上述诗的含义大致相吻合的是( )A、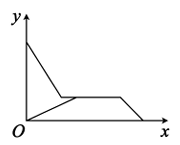 B、
B、 C、
C、 D、
D、 12. 在一定温度下,某固态物质在溶剂中达到饱和状态时所溶解的溶质的质量叫做这种物质在这种溶剂中的溶解度.物质的溶解度会随温度的变化而变化.已知甲、乙两种物质在水中的溶解度与温度之间的对应关系如图所示,相关信息请见下表,则下列说法正确的是( )
12. 在一定温度下,某固态物质在溶剂中达到饱和状态时所溶解的溶质的质量叫做这种物质在这种溶剂中的溶解度.物质的溶解度会随温度的变化而变化.已知甲、乙两种物质在水中的溶解度与温度之间的对应关系如图所示,相关信息请见下表,则下列说法正确的是( )
信息窗
1.溶质质量溶剂质量溶液质量.
2.在一定温度下,向一定量溶剂里加入某种溶质,当溶质不能继续溶解时,所得到的溶液叫做这种溶质的饱和溶液,还能继续溶解的溶液,叫做这种溶质的不饱和溶液.
A、当温度为时,甲物质和乙物质的溶解度都小于 B、当温度从升高至的过程中,甲种物质的溶解度随着温度的升高而增大 C、当时,向水中添加乙,则乙溶液一定能达到饱和状态 D、甲、乙两种物质的溶解度始终都不一样13. 有一个英语单词,其四个字母都关于直线l对称,如图是该单词各字母的一部分,请写出补全后的单词所指的物品:. 14. 汉代初期的《淮南万毕术》记载了我国古代学者在科学领域的成就,下图是古人利用光的反射定律改变光路的方法。在综合实践课上,小圳固定镜面BC , 将镜面BA绕点逆时针转动 , 在光源处发出的一束光射到水平镜面BC后沿DM反射到镜面AB上,随后沿MN反射出去。已知 , 当反射光线MN所在直线与镜面BC所在直线的夹角为时,度。
14. 汉代初期的《淮南万毕术》记载了我国古代学者在科学领域的成就,下图是古人利用光的反射定律改变光路的方法。在综合实践课上,小圳固定镜面BC , 将镜面BA绕点逆时针转动 , 在光源处发出的一束光射到水平镜面BC后沿DM反射到镜面AB上,随后沿MN反射出去。已知 , 当反射光线MN所在直线与镜面BC所在直线的夹角为时,度。 15. 当前我国的军事国防能力稳步提升,特别是激光武器发展迅速.
15. 当前我国的军事国防能力稳步提升,特别是激光武器发展迅速.
(1)如图1,一束激光从点出发,射向轴上的点 , 经过反射后射向点 , 已知光线的反射满足反射定律(即反射角入射角).若点 , 点 , 则直线与轴的交点的坐标为
(2)如图2,线段是一根激光感应器,其函数表达式为 , 从点射出的激光射向位于轴上的镜面 , 经过反射后恰好覆盖线段上的4个整数点(横纵坐标都为整数的点),则的最小值为 .
16. 如图所示是地球截面图,其中 , 分别表示南回归线和北回归线,表示赤道,点P表示某市的位置.现已知地球南回归线的纬度是南纬 , 某市的纬度是北纬 , 而冬至正午时,太阳光直射南回归线(光线的延长线经过地心O),求某市冬至正午时,太阳光线与地面水平线的夹角α的度数 17. 如图1是一架自制天平,支点O固定不变,左侧托盘固定在点A处,右侧托盘的点P可以在横梁段滑动.已知 , , 根据杠杆原理,平衡时:左盘物体质量右盘物体质量(托盘与横梁的质量不计).小慧在存钱罐里存了若干个1元硬币(只有1元硬币),她想利用这个自制天平估计存钱罐里一元硬币的数量.进行了如下操作:
17. 如图1是一架自制天平,支点O固定不变,左侧托盘固定在点A处,右侧托盘的点P可以在横梁段滑动.已知 , , 根据杠杆原理,平衡时:左盘物体质量右盘物体质量(托盘与横梁的质量不计).小慧在存钱罐里存了若干个1元硬币(只有1元硬币),她想利用这个自制天平估计存钱罐里一元硬币的数量.进行了如下操作: (1)、测量一个硬币的质量:如图1,在天平左侧托盘放置一个砝码,右侧托盘放入10个相同的1元硬币,调整点P的位置,发现当时,天平平衡,则测得每个1元硬币的质量为 g;(2)、估算硬币的数量:已知空的存钱罐的质量约为 , 将装了若干个1元硬币的存钱罐放在左侧托盘,右侧托盘放入砝码,调整点P的位置,发现当时,天平向左侧倾斜(如图2),当时,天平向右侧倾斜(如图3),请你帮小慧算一下存钱罐里大约有几个1元硬币?18. 国际上广泛使用“身体体重指数(BMI)”作为判断人体健康状况的一个指标:这个指数B等于人体的体重G(kg)除以人体的身高h(m)的平方所得的商,即B= .
(1)、测量一个硬币的质量:如图1,在天平左侧托盘放置一个砝码,右侧托盘放入10个相同的1元硬币,调整点P的位置,发现当时,天平平衡,则测得每个1元硬币的质量为 g;(2)、估算硬币的数量:已知空的存钱罐的质量约为 , 将装了若干个1元硬币的存钱罐放在左侧托盘,右侧托盘放入砝码,调整点P的位置,发现当时,天平向左侧倾斜(如图2),当时,天平向右侧倾斜(如图3),请你帮小慧算一下存钱罐里大约有几个1元硬币?18. 国际上广泛使用“身体体重指数(BMI)”作为判断人体健康状况的一个指标:这个指数B等于人体的体重G(kg)除以人体的身高h(m)的平方所得的商,即B= .身体体重指数范围
身体属型
B<18
不健康瘦弱
18≤B<20
偏瘦
20≤B<25
正常
25≤B<30
超重
B≥30
不健康肥胖
(1)、上表是国内健康组织提供的参考标准,若林老师体重G=81kg , 身高h=1.80m , 请问他的体型属于哪一种,请说明理由.(2)、赵老师的身高为1.6m , 那么他的体重在什么范围内时,体型属于正常?三、第22题10分,第23题12分,第24题10分,共32分.
-
19. 综合与实践——万花筒里的数学

【发现问题】如图1,学习小组在制作万花筒时,先将两面平面镜的背面用胶带粘贴,形成一个可以自由开合的“镜子门”,发现观察到的图形数量与“镜子门”张角的大小有关,进而研究此规律.
【查阅资料】平面镜成像原理:物体与它在平面镜中的像关于平面镜成轴对称
【数学探究】
探究一:如图2,正方形 P 放在“镜子门”中间,当“镜子门”张角 为 时,正方形 P 关于镜子 OA 的轴对称图形是像 .
(1)、 请你画出正方形 P 在镜子 OB 中的像 (不限作图工具);(2)、 像 , 像 会在镜子中再次轴对称成像,像 关于 的轴对称图形是像 , 像 关于 的轴对称图形是像 , 请分析像 与像 重合(填写“是”或“否”).(3)、探究二:如图3,当“镜子门”张角 大小是 的因数时,观察到的图形数量(包含实物与像,重合的像看作一个像)是有规律的.
改变张角的大小,并记录观察到的图形数量,得到以下表格:
的度数x/度
45
60
72
90
120
观察到的图形数量y/个
8
6
▲
4
3
①在这个变化过程中, ▲ 是自变量, ▲ 是因变量;
②补充上述表格;
③请写出观察到的图形数量y与的度数x的关系式: ▲ .
20. 项目化成果展示了一款简易电子秤:可变电阻上装有托盘(质量忽略不计),测得物品质量x(kg)与可变电阻y(Ω)的多组对应值,画出函数图象(如图1).图2是三种测量方案,电源电压恒为8V,定值电阻为30Ω,与可变电阻串联.
【链接】串联电路中,通过两个电阻的电流I相等,.可变电阻、定值电阻两端的电压之和为8V,则有.
(1)、求y关于x的函数表达式,并写出自变量x的取值范围.(2)、三个托盘放置不同物品后,电表A, , 的读数分别为0.1A,6V,4V.请从以下方案中选择一个,求出对应物品的质量是多少kg?(3)、小明家买了某散装大米65kg,为了检验商家是否存在缺斤少两的情况,请你将大米分批称重,用方案一、二、三来进行检验,设大米为 , 前两次称合适的千克数,第3次用含a的代数式表示,请填写下表.第1次(方案一)
第2次(方案二)
第3次(方案三)
大米(kg)
读数
I= A
= V
V
21. 【背景材料】对称美是我国古人和谐平衡思想的体现,常被用于建筑、器物、绘画、标识等作品的设计上,比如图1.同时,对称在解决生活中的实际问题时,也往往有很大的作用.


【问题提出】某小区要在街道旁修建一个奶站,向居民区A,B提供牛奶,奶站应建在什么地方,才能使A,B到它的距离之和最短?该问题给牛奶公司造成了困扰,现向居民们征求意见.
【问题解决】小明同学将小区和街道抽象出的平面图形,并用轴对称的方法巧妙地解决了这个问题.
如图2,作A关于直线m的对称点 , 连接与直线m交于点C,点C就是所求的位置.



(1)、请你在下列阅读、应用的过程中,完成解答并填空:
证明:如图3,在直线m上另取任一点D,连结 , , ,
∵直线m是点A,的对称轴,点C,D在m上,
∴ , ,
∴ .
在中,
∵ ,
∴ .
∴ , 即最小.
(2)、如图4,在等边中,E是上的点,是的平分线,P是上的点,若 , 则的最小值为 .(3)、【拓展应用】
“龙舟水”来势汹汹,深圳“雨雨雨”模式开启,深圳某学校的志愿者们在查阅地图后,画出了平面示意图5.其中,点A表示龙潭公园,点B表示宝能广场,点C表示万科里,点D表示万科广场,点E表示龙城广场地铁站.如图6,志愿者计划在B宝能广场和D万科广场之间摆放一批共享雨伞,使得共享雨伞的位置到B宝能广场、C万科里、D万科广场和E龙城广场地铁站的距离的和最小.若点A与点C关于对称,请你用尺子在上画出“共享雨伞”的具体摆放位置(用点G表示).