2017-2018学年人教版数学九年级下册28.2 解直角三角形及其应用 同步练习
试卷更新日期:2017-12-14 类型:同步测试
一、单选题
-
1. 在Rt△ABC中,∠C=90°,sinA= ,AB=5,则边AC的长是( )A、3 B、4 C、 D、2.
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米.则小巷的宽度为( )
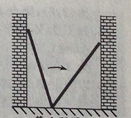 A、0.7米 B、1.5米 C、2.2米 D、2.4米3.
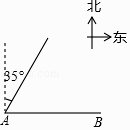
A、0.7米 B、1.5米 C、2.2米 D、2.4米3.如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
 A、北偏东55° B、北偏西55° C、北偏东35° D、北偏西35°4. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )
A、北偏东55° B、北偏西55° C、北偏东35° D、北偏西35°4. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )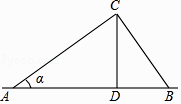 A、 B、 C、 D、h•cosα5. 如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
A、 B、 C、 D、h•cosα5. 如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.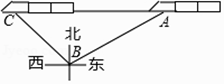 A、20( +1) B、20( ﹣1) C、200 D、3006. 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα= ,则小车上升的高度是( )
A、20( +1) B、20( ﹣1) C、200 D、3006. 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα= ,则小车上升的高度是( ) A、5米 B、6米 C、6.5米 D、12米7. 如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ≈1.414)( )
A、5米 B、6米 C、6.5米 D、12米7. 如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平地面A处安置测倾器测得楼房CD顶部点D的仰角为45°,向前走20米到达A′处,测得点D的仰角为67.5°,已知测倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米, ≈1.414)( )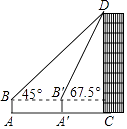 A、34.14米 B、34.1米 C、35.7米 D、35.74米8. 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
A、34.14米 B、34.1米 C、35.7米 D、35.74米8. 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )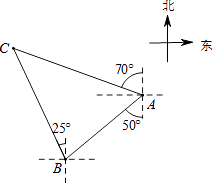 A、10 海里 B、10 海里 C、10 海里 D、20 海里9. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )A、
A、10 海里 B、10 海里 C、10 海里 D、20 海里9. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )A、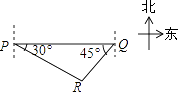 B、
B、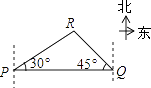 C、
C、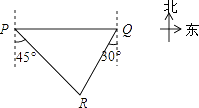 D、
D、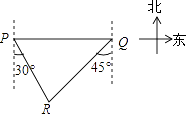 10. 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
10. 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )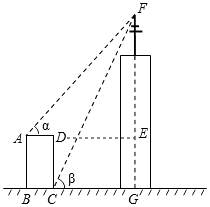 A、(35 +55)m B、(25 +45)m C、(25 +75)m D、(50+20 )m11. 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )
A、(35 +55)m B、(25 +45)m C、(25 +75)m D、(50+20 )m11. 如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为( )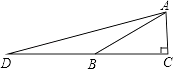 A、2+ B、2 C、3+ D、312. 在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
A、2+ B、2 C、3+ D、312. 在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )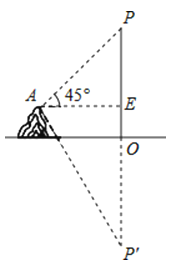 A、25+75 B、50+50 C、75+75 D、50+10013. 如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )
A、25+75 B、50+50 C、75+75 D、50+10013. 如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)( )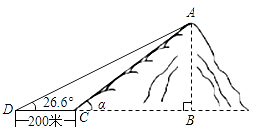 A、164m B、178m C、200m D、1618m14. 如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )A、1,2,3 B、1,1, C、1,1, D、1,2,
A、164m B、178m C、200m D、1618m14. 如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )A、1,2,3 B、1,1, C、1,1, D、1,2,二、填空题
-
15. 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为 n mile.(结果取整数,参考数据: ≈1.7, ≈1.4)
 16. 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为米.
16. 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为米.(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据: ≈1.41, ≈1.73)
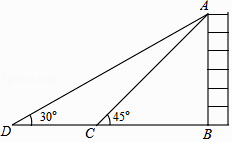 17. △ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是 .18. 为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12 米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE= ,则CE的长为米.
17. △ABC中,AB=12,AC= ,∠B=30°,则△ABC的面积是 .18. 为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12 米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE= ,则CE的长为米. 19.
19.如图,把 个边长为1的正方形拼接成一排,求得 , , ,计算 , ……按此规律,写出 (用含 的代数式表示).
三、解答题
-
20.
如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶中D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(结果精确到0.1m。参考数据:tan20°≈0.36,tan18°≈0.32)
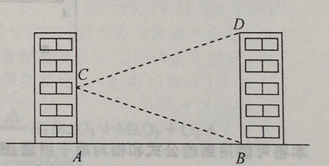 (1)、求∠BCD的度数.(2)、求教学楼的高BD21. 金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73)
(1)、求∠BCD的度数.(2)、求教学楼的高BD21. 金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73) 22. 如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.
22. 如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度. 23. 某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).
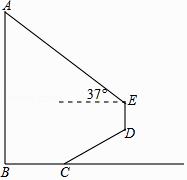
23. 某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).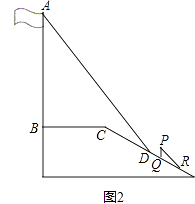 24. 如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方2 米处的点C出发,沿斜面坡度i=1: 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ .计算结果保留根号)
24. 如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方2 米处的点C出发,沿斜面坡度i=1: 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ .计算结果保留根号)