2017-2018学年人教版数学九年级下册28.1 锐角三角函数同步练习

试卷更新日期：2017-12-14 类型：同步测试

进入出卷网下载

一、单选题

1.
如图，已知在 $Rt Δ Α Β C$ 中， $∠ C = 90^{\circ}$ ， $Α Β = 5$ ， $Β C = 3$ ，则 $\cos Β$ 的值是（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
2. $\frac{1}{2}$ sin60°的值等于（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{4}$ D、 $\sqrt{3}$

查看试题解析
3. 为了方便行人推车过某天桥，市政府在10m高的天桥一侧修建了40m长的斜道（如图所示），我们可以借助科学计算器求这条斜道倾斜角的度数，具体按键顺序是（）

A、 B、 C、 D、

查看试题解析
4. 如图，在Rt△ABC中，斜边AB的长为m，∠A=35°，则直角边BC的长是（）

A、msin35° B、mcos35° C、 $\frac{m}{s i n 35 °}$ D、 $\frac{m}{c o s 35 °}$

查看试题解析
5. 在正方形网格中，△ABC的位置如图所示，则cos∠B的值为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、1

查看试题解析
6. 如图，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、3

查看试题解析
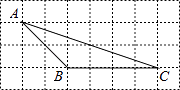7. cos30°的值是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
8. 如图，击打台球时小球反弹前后的运动路线遵循对称原理，即小球反弹前后的运动路线与台球案边缘的夹角相等（α=β），在一次击打台球时，把位于点P处的小球沿所示方向击出，小球经过5次反弹后正好回到点P，若台球案的边AD的长度为4，则小球从P点被击出到回到点P，运动的总路程为（）

A、16 B、16 $\sqrt{2}$ C、20 D、20 $\sqrt{2}$

查看试题解析
9. 如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的是（）

A、 $\frac{B D}{B C}$ B、 $\frac{B C}{A B}$ C、 $\frac{A D}{A C}$ D、 $\frac{C D}{A C}$

查看试题解析
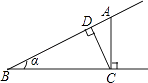10. 一上山坡路（如图所示），小明测得的数据如图中所示，则该坡路倾斜角α的正切值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
11. 如图，点D（0，3），O（0，0），C（4，0）在⊙A上，BD是⊙A的一条弦，则sin∠OBD=（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
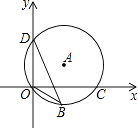12. 一直角三角形的两边长分别为6和8，则该三角形中较小锐角的正弦值为（）

A、 $\frac{3}{5}$ B、 $\frac{\sqrt{7}}{4}$ C、 $\frac{3}{5}$ 或 $\frac{\sqrt{7}}{4}$ D、 $\frac{2}{5}$ 或 $\frac{\sqrt{5}}{4}$

查看试题解析
13. 如果Rt△ABC中各边的长度都扩大到原来的2倍，那么锐角∠A的三角比的值（）

A、都扩大到原来的2倍 B、都缩小到原来的一半 C、没有变化 D、不能确定

查看试题解析
14.
如何求tan75°的值？按下列方法作图可解决问题.如图，在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，延长CB至点M，在射线BM上截取线段BD，使BD=AB，连接AD.连接此图可求得tan75°的值为（）

A、2- $\sqrt{3}$ B、2+ $\sqrt{3}$ C、1+ $\sqrt{3}$ D、 $\sqrt{3}$ -1

查看试题解析

二、计算题

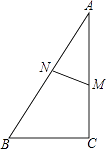
15. 计算：tan²60°﹣2sin30°﹣ $\sqrt{2}$ cos45°．

查看试题解析
16. 如图，在Rt△ABC中，∠C=90°，M是直角边AC上一点，MN⊥AB于点N，AN=3，AM=4，求cosB的值．

查看试题解析
17. 化简：cos²1°+cos²2°+cos²3°+…+cos²89°．

查看试题解析

三、解答题

18. 计算： ${(- 1)}^{2017} - {(- \frac{1}{2})}^{- 3} + {(\cos 68 ° - 2)}^{0} + | 4 \sqrt{3} - 8 \sin 60 ° |$ .

查看试题解析
19. 已知tana= $\frac{3}{4}$ ，求 $\frac{\sin α + \cos α}{\sin α - \cos α}$ 的值．

查看试题解析

四、填空题

20. 在Rt△ABC中，∠C=90°，AB=2，BC= $\sqrt{3}$ ，则sin $\frac{A}{2}$ = ．

查看试题解析
21. 若 $\sqrt{3}$ tan（x+10°）=1，则锐角x的度数为．

查看试题解析
22. 已知对任意锐角α、β均有：cos（α+β）=cosα•cosβ﹣sinα•sinβ，则cos75°= ．

查看试题解析
23. 如图，在下列网格中，小正方形的边长均为1，点A、B、O都在格点上，则∠AOB的正弦值是．

查看试题解析
24. 在Rt△ABC中，∠C=90°，BC= $\sqrt{3}$ ，AC= $\sqrt{6}$ ，则cosA的值是．

查看试题解析

2017-2018学年人教版数学九年级下册28.1 锐角三角函数 同步练习

一、单选题

二、计算题

三、解答题

四、填空题

2017-2018学年人教版数学九年级下册28.1 锐角三角函数同步练习