2017-2018学年人教版数学九年级下册27.3 位似 同步练习
试卷更新日期:2017-12-13 类型:同步测试
一、单选题
-
1. 下列说法错误的是( )
A、位似图形的对应点和位似中心在同一条直线上 B、位似图形上任意一对对应点到位似中心的距离之比等于位似比 C、位似图形一定是相似图形 D、位似图形的对应线段不可能在同一条直线上2. 下列说法正确的是( )
A、相似两个五边形一定是位似图形 B、两个大小不同的正三角形一定是位似图形 C、两个位似图形一定是相似图形 D、所有的正方形都是位似图形3. 如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为( )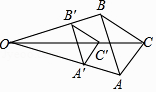 A、2:3 B、3:2 C、4:5 D、4:94. 如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为( )
A、2:3 B、3:2 C、4:5 D、4:94. 如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为( )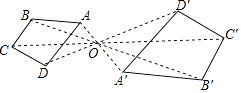 A、4:9 B、2:5 C、2:3 D、 :5. 图中的两个三角形是位似图形,它们的位似中心是( )
A、4:9 B、2:5 C、2:3 D、 :5. 图中的两个三角形是位似图形,它们的位似中心是( )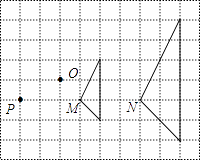 A、点P B、点O C、点M D、点N6. 如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA , 则△ABC与△DEF的面积之比为( )
A、点P B、点O C、点M D、点N6. 如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA , 则△ABC与△DEF的面积之比为( )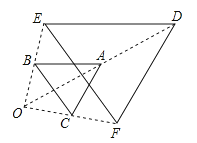 A、1:2 B、1:4 C、1:5 D、1:67. △ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )A、3 B、6 C、9 D、128. 如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )
A、1:2 B、1:4 C、1:5 D、1:67. △ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )A、3 B、6 C、9 D、128. 如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
 A、1 B、2 C、3 D、49. 已知△ABC和△A′B′C′是位似图形.△A′B′C′的面积为6cm2 , △A′B′C′的周长是△ABC的周长一半.则△ABC的面积等于( )A、24cm2 B、12cm2 C、6cm2 D、3cm210.
A、1 B、2 C、3 D、49. 已知△ABC和△A′B′C′是位似图形.△A′B′C′的面积为6cm2 , △A′B′C′的周长是△ABC的周长一半.则△ABC的面积等于( )A、24cm2 B、12cm2 C、6cm2 D、3cm210.如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为( )
 A、(0,0),2 B、(2,2), C、(2,2),2 D、(1,1),11. 如图,已知点E(﹣4,2),点F(﹣1,﹣1),以O为位似中心,把△EFO放大为原来的2倍,则E点的对应点坐标为( )
A、(0,0),2 B、(2,2), C、(2,2),2 D、(1,1),11. 如图,已知点E(﹣4,2),点F(﹣1,﹣1),以O为位似中心,把△EFO放大为原来的2倍,则E点的对应点坐标为( )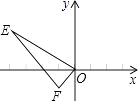 A、(2,﹣1)或(﹣2,1) B、(8,﹣4)或(﹣8,4) C、(2,﹣1) D、(8,﹣4)12. 已知两点A(4,6),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则点A的对应点C的坐标为( )A、(2,3) B、(3,1) C、(2,1) D、(3,3)13.
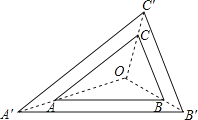
A、(2,﹣1)或(﹣2,1) B、(8,﹣4)或(﹣8,4) C、(2,﹣1) D、(8,﹣4)12. 已知两点A(4,6),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则点A的对应点C的坐标为( )A、(2,3) B、(3,1) C、(2,1) D、(3,3)13.如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=5,则S△A′B′C′等于( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
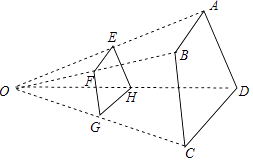
14. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则 = .
 15. 如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是 .
15. 如图,已知图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心的坐标是 .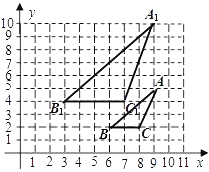 16. 如图,△ABC与△DEF是位似图形,位似比为2:3,已知AB=4,则DE的长为 .
16. 如图,△ABC与△DEF是位似图形,位似比为2:3,已知AB=4,则DE的长为 . 17.
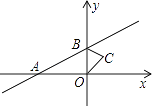
17.如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为 .
 18.
18.已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是 ;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1 ,点C2的坐标是 ;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标 .
三、解答题
-
19. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2 , 并写出C2的坐标.
20.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
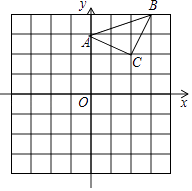 (1)、画出△ABC向下平移4个单位长度得到的△A1B1C1 ,(2)、点C1的坐标是;(3)、以点B为位似中心,在网格内画出△A2B2C2 ,(4)、使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
(1)、画出△ABC向下平移4个单位长度得到的△A1B1C1 ,(2)、点C1的坐标是;(3)、以点B为位似中心,在网格内画出△A2B2C2 ,(4)、使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .


