2017-2018学年人教版数学九年级下册27.2.2 相似三角形的性质 同步练习
试卷更新日期:2017-12-13 类型:同步测试
一、单选题
-
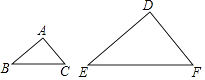
1. 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )
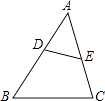
 A、 = B、 = C、 = D、 =2. 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A、 = B、 = C、 = D、 =2. 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( ) A、 = B、 = C、 = D、 =3. 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
A、 = B、 = C、 = D、 =3. 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( ) A、6 B、8 C、10 D、124. 若△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为1:2,则△ABC与△A′B′C′的面积比是( )A、1:1 B、1:2 C、1:3 D、1:45. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A、6 B、8 C、10 D、124. 若△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为1:2,则△ABC与△A′B′C′的面积比是( )A、1:1 B、1:2 C、1:3 D、1:45. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( ) A、 B、 C、 D、6. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A、 B、 C、 D、6. 如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( ) A、
A、 B、
B、 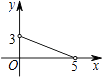 C、
C、 D、
D、 7. 已知△ABC∽△DEF,相似比为3:1,且△DEF的周长为18,则△ABC的周长为( )A、3 B、2 C、6 D、548. 若△ABC∽△A′B′C′,∠A=20°,∠C=120°,则∠B′的度数为( )A、20° B、30° C、40° D、120°9. 若两个相似三角形的面积之比为1:2,则它们的周长之比为( )A、1:2 B、1:4 C、1:3 D、1:10. 如果△ABC∽△A′B′C′,BC=3,B′C′=1.8,则△A′B′C′与△ABC的相似比为( )A、5:3 B、3:2 C、2:3 D、3:511. 如图,点D是△ABC的边AB上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论错误的是( )
7. 已知△ABC∽△DEF,相似比为3:1,且△DEF的周长为18,则△ABC的周长为( )A、3 B、2 C、6 D、548. 若△ABC∽△A′B′C′,∠A=20°,∠C=120°,则∠B′的度数为( )A、20° B、30° C、40° D、120°9. 若两个相似三角形的面积之比为1:2,则它们的周长之比为( )A、1:2 B、1:4 C、1:3 D、1:10. 如果△ABC∽△A′B′C′,BC=3,B′C′=1.8,则△A′B′C′与△ABC的相似比为( )A、5:3 B、3:2 C、2:3 D、3:511. 如图,点D是△ABC的边AB上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论错误的是( ) A、 B、 C、 D、12. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
A、 B、 C、 D、12. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
① CMP∽ BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ;
⑤当 ABP≌ AND时,BP=4 -4.
A、①②③ B、②③⑤ C、①④⑤ D、①②⑤二、填空题
-
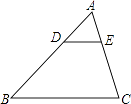
13. 若△ABC∽△A′B′C′,相似比为1:3,则△ABC与△A′B′C′的面积之比为 .14. 如图,在△ABC中,D,E分别为AB,AC上的点,若DE∥BC, = ,则 = .
 15. 如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是 .
15. 如图,在△ABC中,AD平分∠BAC交边BC于点D,BD=AD,AB=3,AC=2,那么AD的长是 .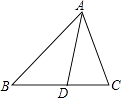 16. 如图,在△ABC中, = ,DE∥AC,则DE:AC= .
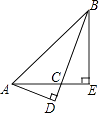
16. 如图,在△ABC中, = ,DE∥AC,则DE:AC= . 17. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 .
17. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 .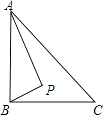
三、解答题
-
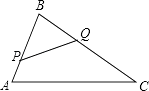
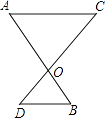
18. 如图,AB与CD相交于点O,△OBD∽△OAC, = ,OB=4,求AO和AB的长.
 19. 已知:如图,在△ABC中,D,E分别是AB,AC上一点,且∠AED=∠B.若AE=5,AB=9,CB=6,求ED的长.
19. 已知:如图,在△ABC中,D,E分别是AB,AC上一点,且∠AED=∠B.若AE=5,AB=9,CB=6,求ED的长.