3.3《 垂径定理》（2）—浙教版数学九年级上册课堂分层训练
试卷更新日期：2025-09-22 类型：同步测试
一、基础应用
-
1. 下列命题正确的是（ ）A、平分一条直径的弦必垂直于这条直径 B、平分一条弧的直线垂直于这条弧所对的弦 C、弦的垂线必经过这条弦所在圆的圆心 D、平分弧的直径垂直平分弧所对的弦2. 如图所示一个圆柱体容器内装入一些水，截面AB在圆心下方，若的直径为 ， 水面宽 ， 则水的最大深度为（ ）
A、 B、 C、 D、3. 小明不慎把家里的圆形镜子打碎了（如图），其中四块碎片如图所示，为了配到与原来大小一样的圆形镜子，小明带到商店去的碎片应该是（ ）
A、① B、② C、③ D、④4. 如图，是的直径，为弦，于点E，则下列结论中不成立的是（ ）
A、 B、 C、 D、5. 如图，为的直径，弦于 ， ， ， 那么弦的长为（ ）
A、 B、 C、 D、6. 如图，某蔬菜基地建蔬菜大棚的剖面，半径 ， 地面宽 ， 则高度为 ．
7. 如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=10，CD=6，则BE=.
8. 如下图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分．如果M是中弦的中点，经过圆心O交圆O于点E，并且 ． 求的半径．
9. “圆”是中国文化的一个重要精神元素，在中式建筑中有着广泛的应用，例如古典园林中的门洞，如图，某地园林中的一个圆弧形门洞的高为2.5m，地面入口宽为1m，求该门洞的半径．
二、能力提升
-
10. 数学活动课上，同学们要测一个如图所示的残缺圆形工件的半径，小明的解决方案是：在工件圆弧上任取两点 ， 连接 ， 作的垂直平分线交于点 ， 交于点 ， 测出 ， 则圆形工件的半径为（ ）
A、 B、 C、 D、11. 如图，MN所在的直线垂直平分线段AB，利用这样的工具，可以找到圆形工件的圆心．如果使用此工具找到圆心，则最少使用的次数为( )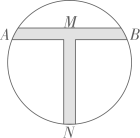
A、1 B、2 C、3 D、412. 如图，⊙O的弦AB，AC的夹角为50°，M，N分别为和的中点，0M，ON分别交AB，AC于点E，F，则∠MON的度数为( )
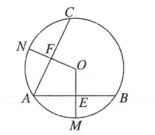A、110° B、120 C、130° D、100°13. 如图，石拱桥的主桥拱是圆弧形．如图，一石拱桥的跨度AB＝16m ， 拱高CD＝4m ， 那么桥拱所在圆的半径OA＝m ．
14. 一条排水管横截面如图所示，已知排水管半径 ， 水面宽 ， 若管内水面下降 ， 则此时水面宽等于m．
15. 已知：如图，在⊙O中， ． 求证：弦AB∥CD．
16. 如图，AB，AC是⊙O的两条弦，M，N分别为 ， 的中点，MN分别交AB，AC于点E，F．判断△AEF的形状并给予证明．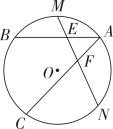
17. 某村为了促进农村经济发展，建设了蔬菜基地，新建了一批蔬菜大棚．如图是蔬菜大棚的截面，形状为圆弧型，圆心为 ， 跨度（弧所对的弦）的长为8米，拱高（弧的中点到弦的距离）为2米．
(1)、求该圆弧所在圆的半径；(2)、在修建过程中，在距蔬菜大棚的一端（点）1米处将竖立支撑杆 ， 求支撑杆的高度．三、综合拓展
-
18. “筒车”是一种以水流作动力，取水罐田的工具，点表示筒车的一个盛水桶，如图①．明朝科学家徐光启在《农政全书》中用图绘出了“筒车”的工作原理，如图②．当筒车工作时，盛水桶的运行路径是以轴心为圆心的一个圆，且圆心始终在水面上方．若圆被水面截得的弦长为 ， 水面下盛水桶的最大深度（即水面下方圆上的点距离水面的最大距离）为2米．
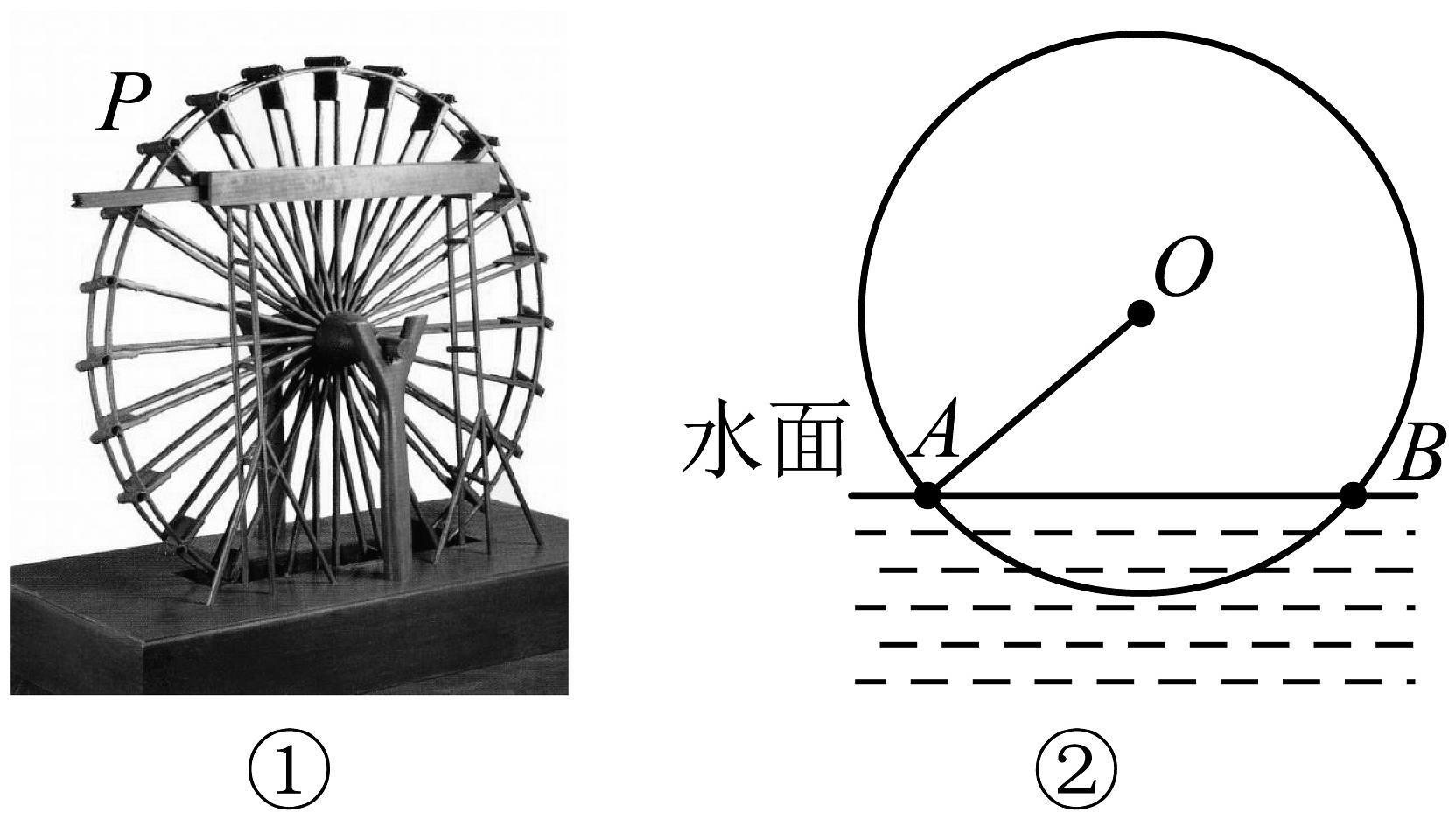(1)、求该圆的半径．(2)、若水面下降导致圆被水面截得的弦的长度从原来的8米变为6米，则水面下盛水桶的最大深度为多少米？19. 某地欲搭建一桥，桥的底部两端间的距离称跨度，桥面最高点到的距离称拱高，当和确定时，有两种设计方案可供选择；①抛物线型；②圆弧型．已知这座桥的跨度米，拱高米．
(1)、如图1，若设计成抛物线型，以所在直线为轴，的垂直平分线为轴建立坐标系，求此函数表达式；(2)、如图2，若设计成圆弧型，求该圆弧所在圆的半径；(3)、现有一艘宽为15米的货船，船舱顶部为方形，并高出水面2.2米．从以上两种方案中，任选一种方案，判断此货船能否顺利通过你所选方案的桥？并说明理由．