人教版数学八年级上学期期中仿真模拟试卷四(范围:13.1-15.3)
试卷更新日期:2025-09-22 类型:期中考试
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 下列四种图案中,可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,已知图中的两个三角形全等,则的度数是( )
2. 如图,已知图中的两个三角形全等,则的度数是( ) A、 B、 C、 D、3. 如图,在中, , , 是边上的两点, , 平分 , 下列说法不正确的是( )
A、 B、 C、 D、3. 如图,在中, , , 是边上的两点, , 平分 , 下列说法不正确的是( ) A、是的中线 B、 C、是的角平分线 D、是的高4. 如图,△AOC与△BOD全等.已知∠A与∠B是对应角,则对其余对应边或对应角判断错误的是( )
A、是的中线 B、 C、是的角平分线 D、是的高4. 如图,△AOC与△BOD全等.已知∠A与∠B是对应角,则对其余对应边或对应角判断错误的是( ) A、对应边:OA与OB B、对应边:AC与BD C、对应角:∠OCA与∠ODB D、对应角:∠AED与∠BEC5. 如图,在▱ABCD中,AB=8cm , AD=5cm , AE和BF分别是∠BAD和∠ABC的角平分线,交CD于点E和点F , 则线段EF的长度为( )
A、对应边:OA与OB B、对应边:AC与BD C、对应角:∠OCA与∠ODB D、对应角:∠AED与∠BEC5. 如图,在▱ABCD中,AB=8cm , AD=5cm , AE和BF分别是∠BAD和∠ABC的角平分线,交CD于点E和点F , 则线段EF的长度为( ) A、3cm B、2cm C、1cm D、2.5cm6. 在联欢晚会上,有、、三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在的( )A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三条垂直平分线的交点7. 如图,在△ABC 中,∠BAC=90°,AB=3,AC=4,D为BC上一点,过点A作AE∥BC,连接DE交AC于点 F,若AE=CD,则图中阴影部分的面积为 ( )
A、3cm B、2cm C、1cm D、2.5cm6. 在联欢晚会上,有、、三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在的( )A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三条垂直平分线的交点7. 如图,在△ABC 中,∠BAC=90°,AB=3,AC=4,D为BC上一点,过点A作AE∥BC,连接DE交AC于点 F,若AE=CD,则图中阴影部分的面积为 ( ) A、6 B、12 C、18 D、248. 如图,在中, , 分别平分和 , , 相交于点P,则下列结论不一定成立的是( )
A、6 B、12 C、18 D、248. 如图,在中, , 分别平分和 , , 相交于点P,则下列结论不一定成立的是( ) A、 B、与的面积比等于边与之比 C、 D、若 , 则9. 通过如下尺规作图,能说明的面积和的面积相等的是( )A、
A、 B、与的面积比等于边与之比 C、 D、若 , 则9. 通过如下尺规作图,能说明的面积和的面积相等的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在△ABC中,∠ACB=60°,AG平分∠BAC交BC与点G , BD平分∠ABC交AC于点D , AG、BD相交于点F , BE⊥AG交AG的延长线于点E , 连接CE , 下列结论中正确的是( )
10. 如图,在△ABC中,∠ACB=60°,AG平分∠BAC交BC与点G , BD平分∠ABC交AC于点D , AG、BD相交于点F , BE⊥AG交AG的延长线于点E , 连接CE , 下列结论中正确的是( )
①若∠BAD=70°,则∠EBC=5°;②BF=2EF;③BE=CE;④AB=BG+AD .
A、4个 B、3个 C、2个 D、1个二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 如图,∠ACD是△ABC的外角,若∠ACD=110°,∠A=80°,则∠B=°.
 12. 已知是的中线,若与的周长分别为 , , 则 .13. 如图,在中, , 点是上一点, , 则度.
12. 已知是的中线,若与的周长分别为 , , 则 .13. 如图,在中, , 点是上一点, , 则度. 14. 如图,为内一点,平分 , , , 若 , , 则的长为 .
14. 如图,为内一点,平分 , , , 若 , , 则的长为 .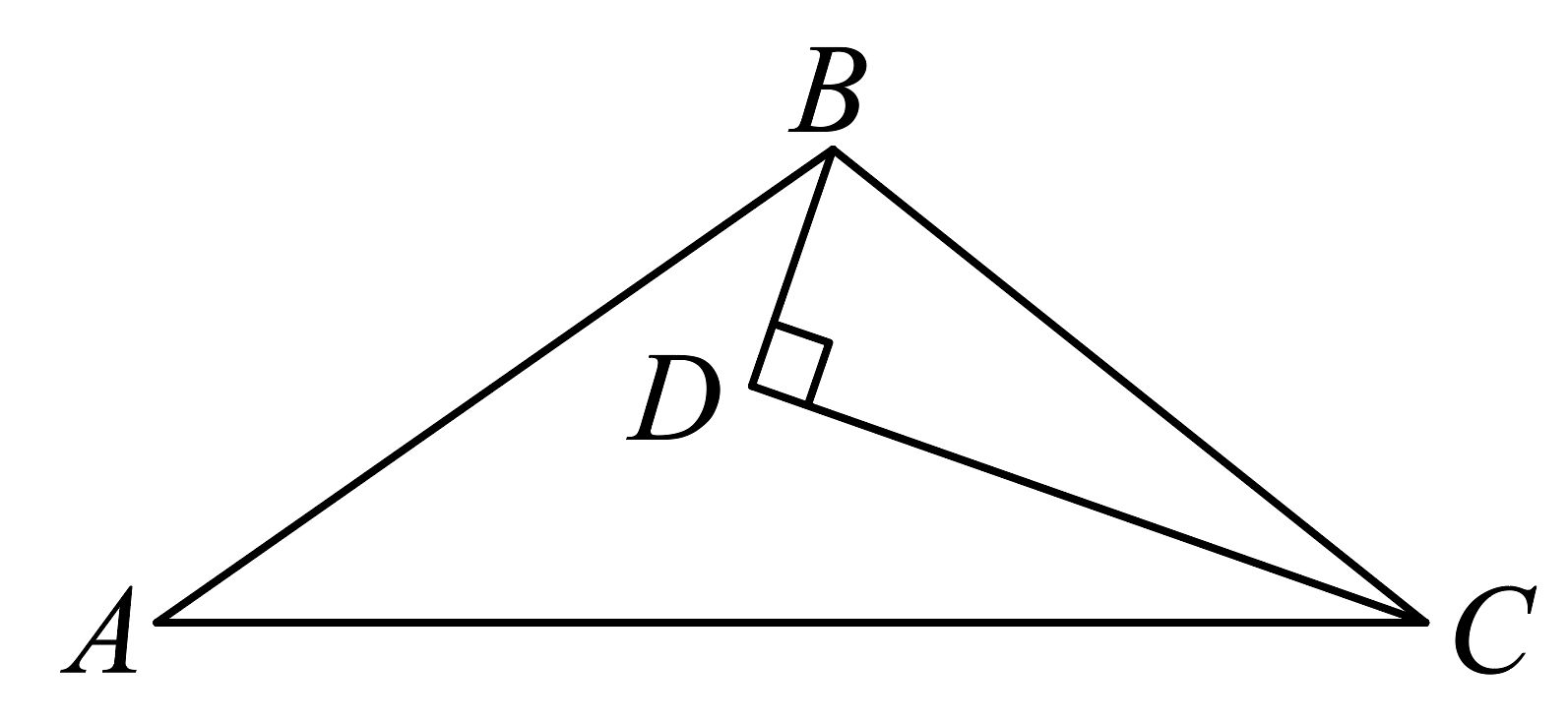 15. 如图,在中, , , D为平面上一点, , 若 , 则的面积为.
15. 如图,在中, , , D为平面上一点, , 若 , 则的面积为. 16. 小王在探究等边三角形“手拉手”问题,得出以下四个结论.
16. 小王在探究等边三角形“手拉手”问题,得出以下四个结论.如图 , 已知 , 均为等边三角形,点在线段上,且不与点、点重合,连接 , 则;
已知条件同 , 则;
如图 , 已知 , 均为等边三角形,点在内部,连接、 , 则、、三点共线;
如图 , 已知为等边三角形,点在外,并且与点位于线段的异侧,连接、 . 若 , 则 .
以上结论正确的是 .

三、解答题:本大题共9小题,共75分.
-
17. 已知:△ABC 的三个顶点坐标A(-2,0),B(5,0),C(4,3).
 (1)、在平面直角坐标系中画出△ABC ,先将△ABC关于x轴作轴对称,得到△A’B’C’ , 再将△A’B’C’向左平移3个单位,得到△A”B”C” , 写出C”的坐标;(2)、求出△ABC 的面积.18. 如图,在△ABC中,AB=AC,∠1=∠2。△ABD与△ACD全等吗?证明你的判断。
(1)、在平面直角坐标系中画出△ABC ,先将△ABC关于x轴作轴对称,得到△A’B’C’ , 再将△A’B’C’向左平移3个单位,得到△A”B”C” , 写出C”的坐标;(2)、求出△ABC 的面积.18. 如图,在△ABC中,AB=AC,∠1=∠2。△ABD与△ACD全等吗?证明你的判断。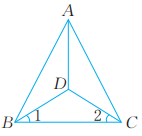 19. 如图,和都是等边三角形,且B , C , D三点在一条直线上,连接 , 相交于点P .
19. 如图,和都是等边三角形,且B , C , D三点在一条直线上,连接 , 相交于点P . (1)、求证:;(2)、求的度数.20. 如图所示,AC平分∠BCD,AB=AD,AE⊥BC于点E,AF⊥CD于点F.
(1)、求证:;(2)、求的度数.20. 如图所示,AC平分∠BCD,AB=AD,AE⊥BC于点E,AF⊥CD于点F. (1)、若∠ABE=60°,求∠CDA 的度数.(2)、若AE=2,BE=1,CD=4.求四边形ABCD 的面积.21. 如图,中, , , 是由绕点按逆时针方向旋转得到的,连接、相交于点 , 与相交于点 .
(1)、若∠ABE=60°,求∠CDA 的度数.(2)、若AE=2,BE=1,CD=4.求四边形ABCD 的面积.21. 如图,中, , , 是由绕点按逆时针方向旋转得到的,连接、相交于点 , 与相交于点 . (1)、求证:;(2)、求的度数.22. 在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.
(1)、求证:;(2)、求的度数.22. 在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.(1)如图1,若点E为AB的中点,求证:AE=DB;
(2)如图2,若点E为AB上任意一点,猜想AE与DB的数量关系,并证明你的猜想.
 23. 【实际情境】
23. 【实际情境】手工课堂上,老师给每个制作小组发放一把花折伞和制作花折伞的材料及工具.同学们认真观察后,组装了花折伞的骨架,粘贴了彩色伞面,制作出精美的花折伞.
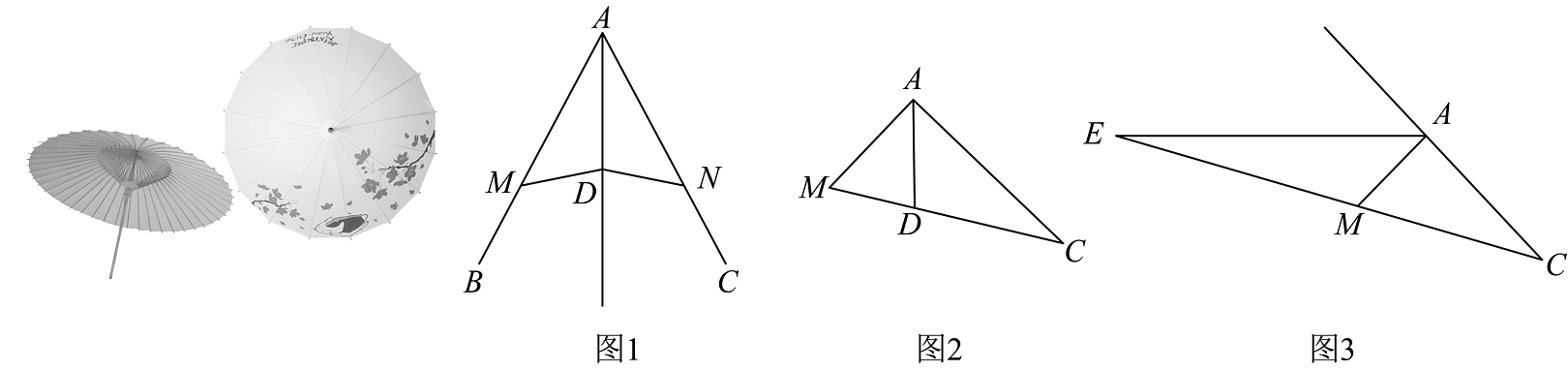
【问题初探】
(1)如图1,从花折伞中抽象出“牵形图”, , . 求证: .
【方法迁移】
(2)如图2,中,的平分线交于点 . 请你从以下两个条件:
①;②中选择一个作为已知条件,另一个作为结论,并写出结论成立的证明过程.(注:只需选择一种情况作答.)
【问题拓展】
(3)如图3,在中, , 是的外角的平分线,交的延长线于点 . 请你直接写出线段之间的数量关系.
24. 【问题呈现】小明在学习了三角形有关内角与外角的相关知识后遇到这样一个问题:如图①,与分别为的两个外角,则 .【推理证明】∵与分别为的两个外角,
∴______,______,
∴______.
∵ ,
∴ .
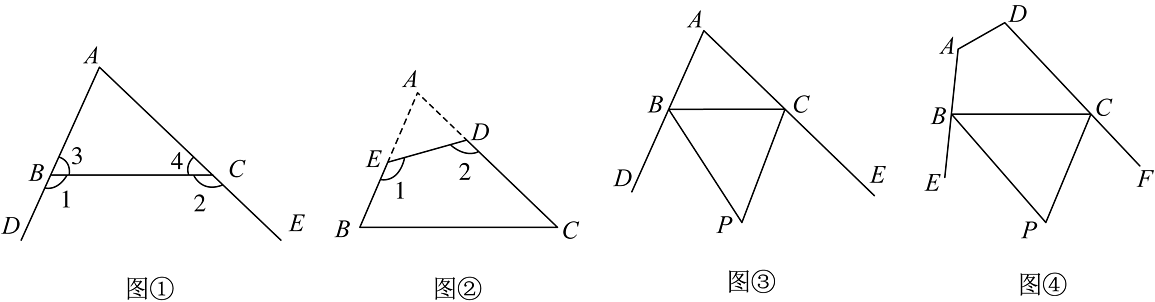
【初步应用】
(1)如图②,在纸片中剪去 , 得到四边形 , 若 , 则的大小为______度.
(2)如图③,在中,、分别为外角、的平分线,则与的数量关系,并说明理由.
【拓展提升】
(3)如图④,在四边形中,、分别为外角、的平分线,若 , 求的度数.