人教版数学八年级上学期期中仿真模拟试卷三(范围:13.1-15.3)
试卷更新日期:2025-09-22 类型:期中考试
一、选择题
-
1. 如图,三角形有一部分被遮挡,我们可以判定此三角形的类型为( )
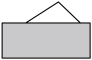 A、钝角三角形 B、直角三角形 C、锐角三角形 D、不能确定2. 下列各图中,作△ABC边AB上的高,正确的是 ( )A、
A、钝角三角形 B、直角三角形 C、锐角三角形 D、不能确定2. 下列各图中,作△ABC边AB上的高,正确的是 ( )A、 B、
B、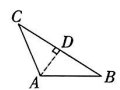 C、
C、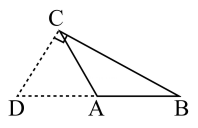 D、
D、 3. 如图,在中, , , 是的外角,则的度数是( )
3. 如图,在中, , , 是的外角,则的度数是( ) A、 B、 C、 D、4. 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
A、 B、 C、 D、4. 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( ) A、三边中线的交点 B、三条角平分线的交点 C、三边高的交点 D、三边垂直平分线的交点5. 如图是嘉嘉为参加手工比赛制作燕子风筝的骨架图,已知AC=AD,AB=AE,∠BAD=∠EAC,∠D=35°,则∠C的度数为 ( )
A、三边中线的交点 B、三条角平分线的交点 C、三边高的交点 D、三边垂直平分线的交点5. 如图是嘉嘉为参加手工比赛制作燕子风筝的骨架图,已知AC=AD,AB=AE,∠BAD=∠EAC,∠D=35°,则∠C的度数为 ( ) A、30° B、35° C、40° D、45°6. 在中, , . 用无刻度的直尺和圆规在BC边上找一点 , 使为等腰三角形.下列作法不正确的是( )A、
A、30° B、35° C、40° D、45°6. 在中, , . 用无刻度的直尺和圆规在BC边上找一点 , 使为等腰三角形.下列作法不正确的是( )A、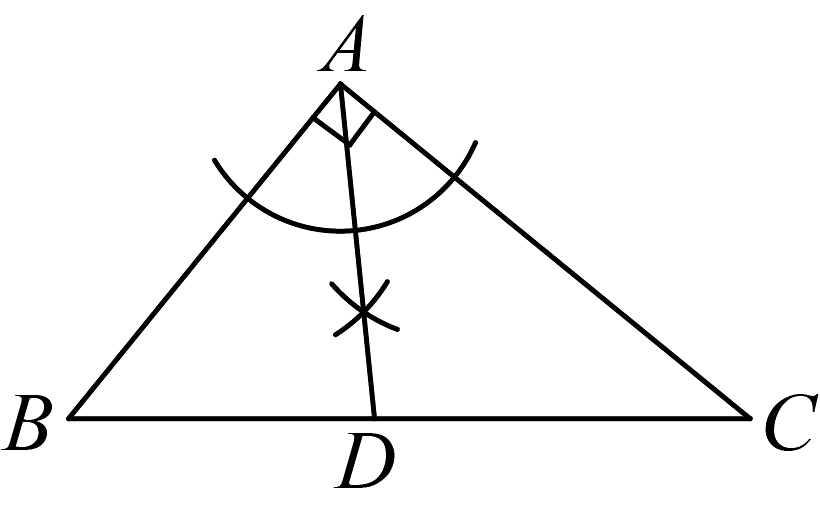 B、
B、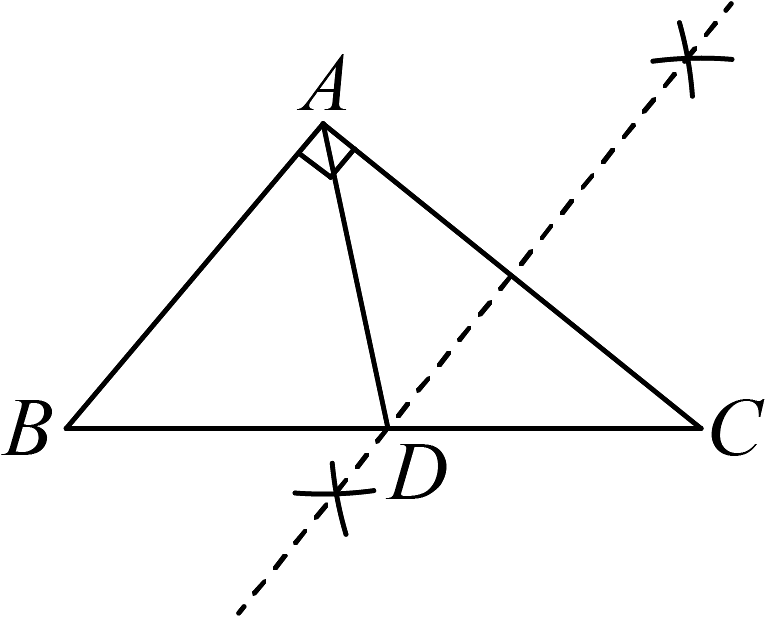 C、
C、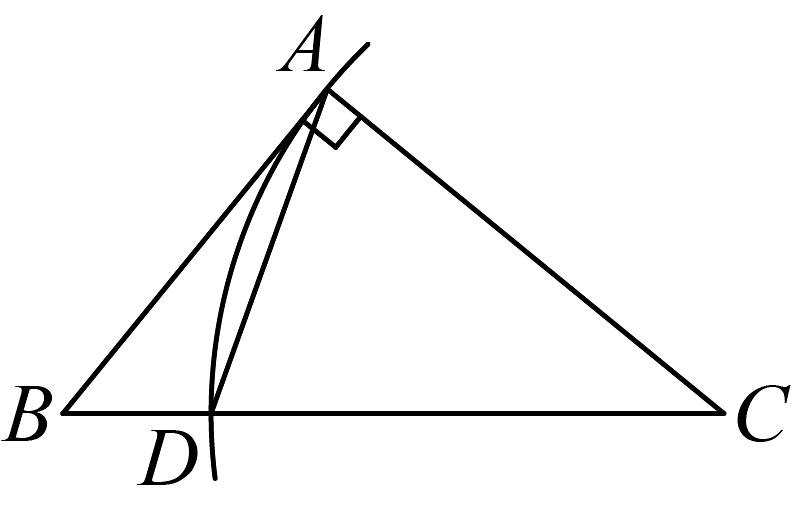 D、
D、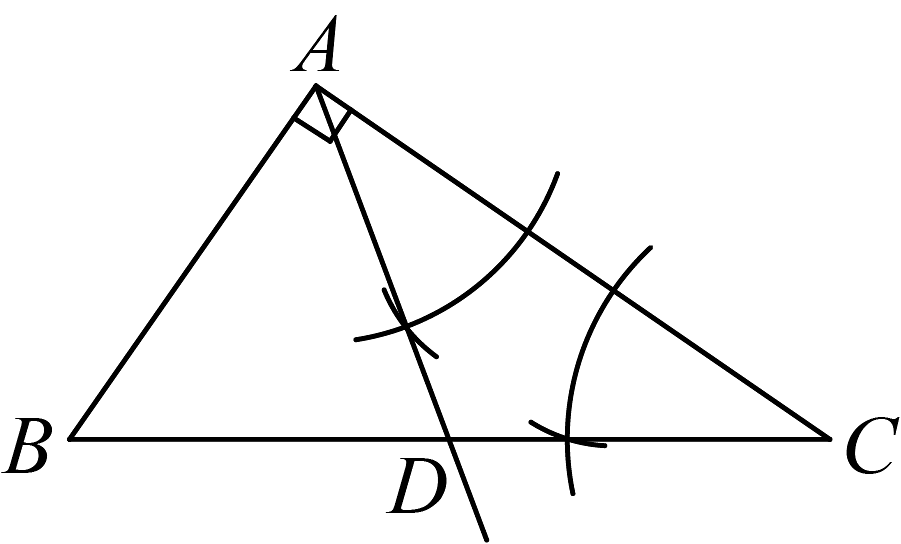 7. 如图,在△ABC中,BC 的垂直平分线分别交AC,BC 于点 D,E,连接BD,若△ABC 的周长为20,CE=4,则△ABD的周长为 ( )
7. 如图,在△ABC中,BC 的垂直平分线分别交AC,BC 于点 D,E,连接BD,若△ABC 的周长为20,CE=4,则△ABD的周长为 ( ) A、12 B、14 C、16 D、188. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、9. 如图,A、C、B三点在同一条直线上,和都是等边三角形,分别与交于点M、N,有如下结论:①;②;③;④是等边三角形;其中,正确结论的个数是( )
A、12 B、14 C、16 D、188. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、9. 如图,A、C、B三点在同一条直线上,和都是等边三角形,分别与交于点M、N,有如下结论:①;②;③;④是等边三角形;其中,正确结论的个数是( )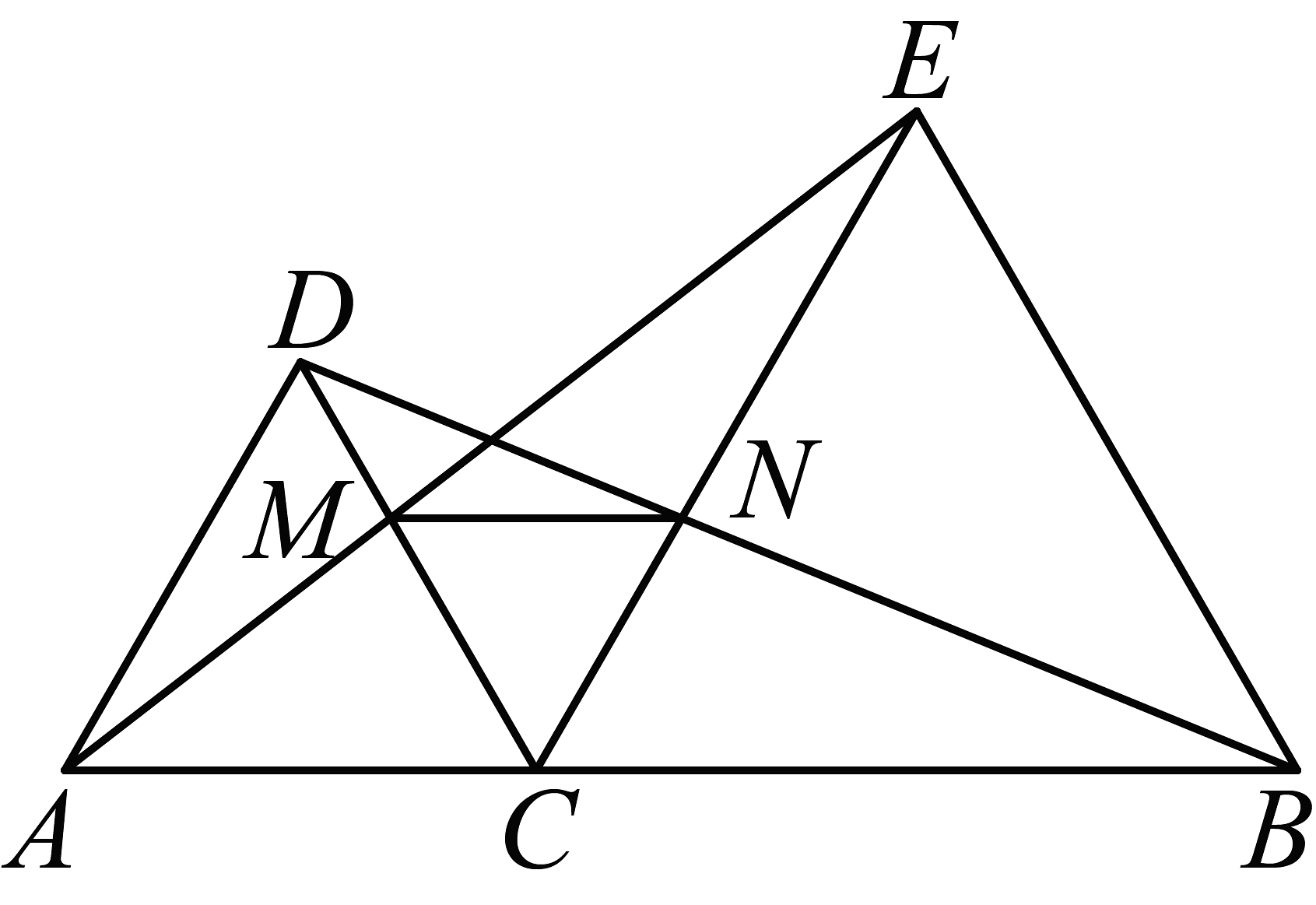 A、1个 B、2个 C、3个 D、4个10. 如图,已知, , 点、、…在射线上,点、、在射线上,、、、均为等边三角形,若 , 则的边长为( )
A、1个 B、2个 C、3个 D、4个10. 如图,已知, , 点、、…在射线上,点、、在射线上,、、、均为等边三角形,若 , 则的边长为( ) A、16 B、32 C、64 D、128
A、16 B、32 C、64 D、128二、填空题
-
11. 已知等腰三角形的周长为15,其中一边的长为3,则该等腰三角形的腰长是.12. 一副三角板,按如图所示方式叠放在一起,则图中 .
 13. 如图,在△ABC中, , 是边上的中线,若的面积为3,则的面积是 .
13. 如图,在△ABC中, , 是边上的中线,若的面积为3,则的面积是 . 14. 一个三角形的三边为3,5,x,另一个三角形的三边为y,3,6,如果这两个三角形全等,那么x+y=.15. 在中, , 点D是直线上一点(不与B、C重合),以为一边在=的右侧作 , 使 , , 连接 .
14. 一个三角形的三边为3,5,x,另一个三角形的三边为y,3,6,如果这两个三角形全等,那么x+y=.15. 在中, , 点D是直线上一点(不与B、C重合),以为一边在=的右侧作 , 使 , , 连接 .
(1)如图1,当点在线段上,如果 , 则度;
(2)点D在直线上移动,若 , . 则α,β之间的数量关系为 .
16. 如图, 中, , , ,点 是 上一动点,以 为边在 的右侧作等边 , 是 的中点,连结 ,则 的最小值是.
三、解答题
-
17. 在如图所示方格纸中,每个小正方形的边长均为1,点A,B,C在小正方形的顶点上.

⑴画出△ABC中BC边上的高线AD.
⑵画出△ABC中AC边,上的中线BE.
⑶△ABE的面积为 ▲
18. 如图:△ABC中,AC>AB. (1)、作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ.(尺规作图,保留作图痕迹,不需要写作法)(2)、在(1)的条件下,若BC=14,求△APQ的周长.19. 如图,在△ABC中,AD⊥BC于点D,BD=CD。完成下面说明∠B=∠C的理由的过程(填空)。
(1)、作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ.(尺规作图,保留作图痕迹,不需要写作法)(2)、在(1)的条件下,若BC=14,求△APQ的周长.19. 如图,在△ABC中,AD⊥BC于点D,BD=CD。完成下面说明∠B=∠C的理由的过程(填空)。
解:由AD⊥BC(已知),
得∠ADB==Rt∠(垂直的定义)。
当把图形沿AD对折时,射线DB与DC。
由BD=CD (),
可知点B与点重合,
所以△ABD与△ACD ,
即△ABD△ACD(全等三角形的定义),
所以∠B=∠C ()。
20. 如图,在中,是边上的高,是的角平分线, , .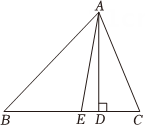 (1)、求的度数;(2)、求的度数.21. 如图,在中, , 于点 , , 点在上, .
(1)、求的度数;(2)、求的度数.21. 如图,在中, , 于点 , , 点在上, . (1)、求证:平分;(2)、求证: .22. 如图,四边形中,度,E是上一点,且 ,
(1)、求证:平分;(2)、求证: .22. 如图,四边形中,度,E是上一点,且 , (1)、与全等吗?请说明理由;(2)、求证: .23. (1)如图1,在中, , , 是边上的中线,延长到点使 , 连接 , 把 , , 集中在中,利用三角形三边关系可得的取值范围.请写出的取值范围,并说明理由.
(1)、与全等吗?请说明理由;(2)、求证: .23. (1)如图1,在中, , , 是边上的中线,延长到点使 , 连接 , 把 , , 集中在中,利用三角形三边关系可得的取值范围.请写出的取值范围,并说明理由.(2)如图2,在中,是边上的中线,点 , 分别在 , 上,且 , 求证: . 小艾同学受到(1)的启发,在解决(2)的问题时,延长到点 , 使…,请你帮她完成证明过程.
(3)如图3,在四边形中,为钝角,为锐角, , , , 点 , 分别在 , 上,且 , 连接 , 试探索线段 , , 之间的数量关系,并加以证明.
 24. 如图,在直角坐标系中,点 , 点B为x轴正半轴上一个动点,以为边作 , 使 , 且点C在第一象限内.
24. 如图,在直角坐标系中,点 , 点B为x轴正半轴上一个动点,以为边作 , 使 , 且点C在第一象限内.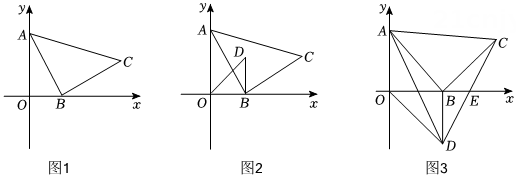 (1)、如图1,若 , 求点C的坐标.(2)、如图2,过点B向x轴上方作 , 且 , 在点B的运动过程中,探究点C,D之间的距离是否为定值.若为定值,求出该定值,若不是,请说明理由.(3)、如图3,过点B向x轴下方作 , 且 , 连结交x轴于点E,当的面积是的面积的2倍时,求的长.
(1)、如图1,若 , 求点C的坐标.(2)、如图2,过点B向x轴上方作 , 且 , 在点B的运动过程中,探究点C,D之间的距离是否为定值.若为定值,求出该定值,若不是,请说明理由.(3)、如图3,过点B向x轴下方作 , 且 , 连结交x轴于点E,当的面积是的面积的2倍时,求的长.