专题3一线三等角全等模型-浙教版数学八年级上册解题模型
试卷更新日期:2025-09-22 类型:复习试卷
一、选择题
-
1. 如图,四边形 ABCD 是正方形,BE⊥EF,DF⊥EF,BE=2.5cm ,DF=4 cm,那么 EF 的长为 ( )
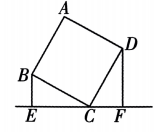 A、6.5 cm B、6 cm C、5.5 cm D、4 cm2. 如图,将正方形先向右平移,使点B与原点O重合,再将所得正方形绕原点O顺时针方向旋转 , 得到四边形 , 则点A的对应点的坐标是( )
A、6.5 cm B、6 cm C、5.5 cm D、4 cm2. 如图,将正方形先向右平移,使点B与原点O重合,再将所得正方形绕原点O顺时针方向旋转 , 得到四边形 , 则点A的对应点的坐标是( )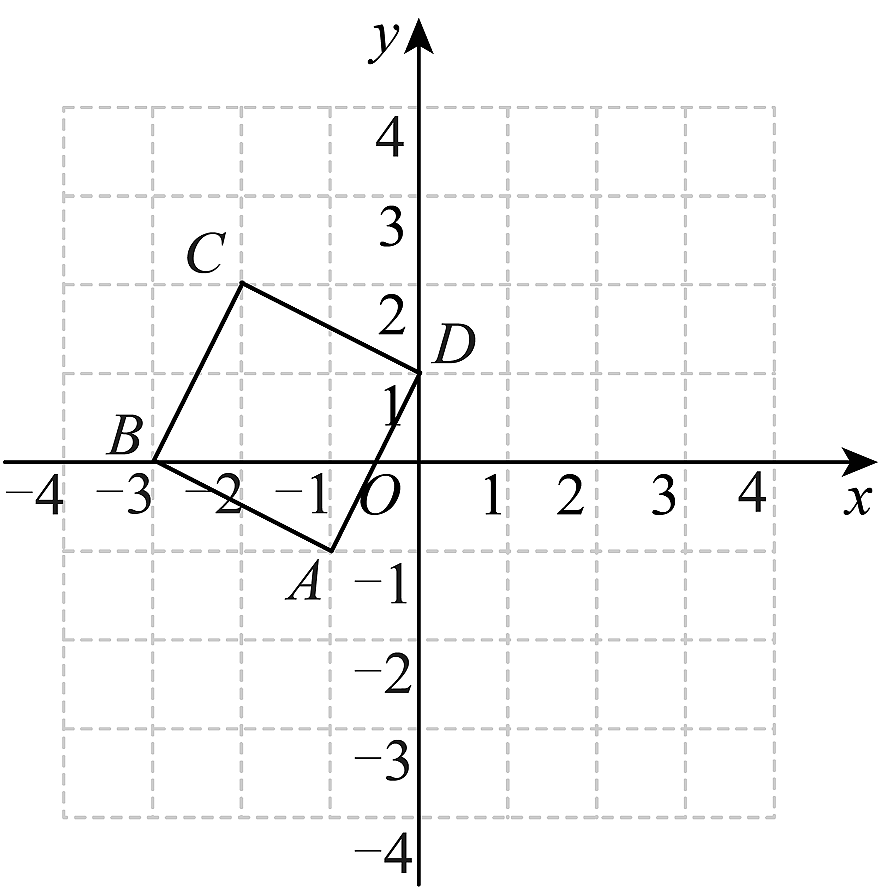 A、 B、 C、 D、3. 如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE ⊥DE ,则△BDC通过下列变换能与△ACE重合的是( )
A、 B、 C、 D、3. 如图,△ABC是等腰直角三角形,DE是过点C的直线,BD⊥DE,AE ⊥DE ,则△BDC通过下列变换能与△ACE重合的是( ) A、绕点C逆时针旋转90度 B、沿AB的垂直平分线翻折 C、绕AB的中点M顺时针旋转90度 D、沿DE方向平移4. 小丽与爸妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她,若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m, , 爸爸在C处接住小丽时,小丽距离地面的高度是( )
A、绕点C逆时针旋转90度 B、沿AB的垂直平分线翻折 C、绕AB的中点M顺时针旋转90度 D、沿DE方向平移4. 小丽与爸妈在公园里荡秋千,如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她,若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m, , 爸爸在C处接住小丽时,小丽距离地面的高度是( ) A、1.4m B、1.6m C、1.7m D、1.8m5. 如图,在△ABC,∠C=90°,AD平分∠BAC交CB于点D,过点D作DE⊥AB,垂足恰好是边AB的中点E,若AD=3cm,则BE的长为( )
A、1.4m B、1.6m C、1.7m D、1.8m5. 如图,在△ABC,∠C=90°,AD平分∠BAC交CB于点D,过点D作DE⊥AB,垂足恰好是边AB的中点E,若AD=3cm,则BE的长为( ) A、 cm B、4cm C、3 cm D、6cm
A、 cm B、4cm C、3 cm D、6cm二、填空题
-
6. 如图,直线 , , 分别过正方形的三个顶点 , , , 且相互平行,若 , 的距离为 , , 的距离为 , 则正方形的面积为 .
 7. 如图,在中, , M是的中点,点D在上, , , 垂足分别为E,F,连接 , 则下列结论中:①;②;③;④ . 正确的有 . (只填序号)
7. 如图,在中, , M是的中点,点D在上, , , 垂足分别为E,F,连接 , 则下列结论中:①;②;③;④ . 正确的有 . (只填序号) 8. 如图,以的边、为腰分别向外作等腰直角、 , 连结、、 , 过点的直线分别交线段、于点、 , 以下说法:①当时,;②;③若 , , , 则;④当直线时,点为线段的中点.正确的有 . (填序号)
8. 如图,以的边、为腰分别向外作等腰直角、 , 连结、、 , 过点的直线分别交线段、于点、 , 以下说法:①当时,;②;③若 , , , 则;④当直线时,点为线段的中点.正确的有 . (填序号)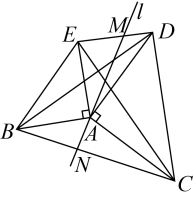 9. 如图,在Rt中,是的平分线,将BD以为中心,逆时针旋转 , 点的对应点为 . 则AE的长度为 .
9. 如图,在Rt中,是的平分线,将BD以为中心,逆时针旋转 , 点的对应点为 . 则AE的长度为 . 10. 如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=cm.
10. 如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=cm. 11. 如图中, , , , 将边绕点 B顺时针旋转90°至 , 连 , 则 .
11. 如图中, , , , 将边绕点 B顺时针旋转90°至 , 连 , 则 .
三、解答题
-
12. 小甬按如图方式测量旗杆高度AB,将A处的绳子笔直拉至地面C处,使B,C间距离等于小甬直立时的眼睛离地高度,在C处放置一块直角三角板PMN,使直角顶点P落在C处,边PN与绳子重合,随后小甬后退至D处直立,使眼睛E与点M,P在同一直线上.小甬认为CD的长等于旗杆高度AB,你认同他的观点吗?请说明理由.
 13. 如图,在四边形中,是边上一点, , 求证: .
13. 如图,在四边形中,是边上一点, , 求证: . 14. 综合与探究
14. 综合与探究 (1)、模型建立:如图1,等腰Rt中, , 直线ED经过点 , 过点作于点 , 过点作于点 .
(1)、模型建立:如图1,等腰Rt中, , 直线ED经过点 , 过点作于点 , 过点作于点 .求证:;
(2)、模型应用:①如图2,已知直线与轴交于点,与轴交于点,将线段AB绕点逆时针旋转 , 得到线段BC , 过点A , C作直线,求直线AC的函数解析式;
②如图3,长方形ABCO , 点为坐标原点,点的坐标为分别在坐标轴上,点是线段BC上动点,已知点在第一象限,且是直线上的一点,若是不以点为直角顶点的等腰直角三角形,请直接写出所有符合条件的点的坐标.
15. 综合运用: (1)、【模型建立】如图1,等腰中, , , 直线经过点C , 过点A作于点D , 过点B作于点E , 求证: .(2)、【模型应用】如图2,已知直线与x轴交于点A , 与y轴交于点B , 将直线绕点A逆时针旋转至直线 , 求直线的函数表达式;16. 小明同学在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆的点O处用一根细绳悬挂一个小球 , 小球可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点作于点 , 当小球摆到OC位置时,OB与OC恰好垂直(图中A、B、O、C在同一平面上),过点C作于点 , 测得.
(1)、【模型建立】如图1,等腰中, , , 直线经过点C , 过点A作于点D , 过点B作于点E , 求证: .(2)、【模型应用】如图2,已知直线与x轴交于点A , 与y轴交于点B , 将直线绕点A逆时针旋转至直线 , 求直线的函数表达式;16. 小明同学在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆的点O处用一根细绳悬挂一个小球 , 小球可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点作于点 , 当小球摆到OC位置时,OB与OC恰好垂直(图中A、B、O、C在同一平面上),过点C作于点 , 测得. (1)、求证:;(2)、求AE的长.17. 三个等角的顶点在同一条直线上,称一线三等角模型(角度有锐角、直角、钝角,若为直角,则又称一线三垂直模型),解决此模型问题的一般方法是利用三等角关系找全等三角形所需角的相等条件,利用全等三角形解决问题.
(1)、求证:;(2)、求AE的长.17. 三个等角的顶点在同一条直线上,称一线三等角模型(角度有锐角、直角、钝角,若为直角,则又称一线三垂直模型),解决此模型问题的一般方法是利用三等角关系找全等三角形所需角的相等条件,利用全等三角形解决问题.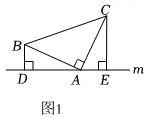
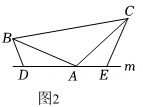
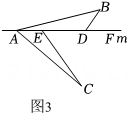 (1)、如图1,在中, , , 直线经过点 , 直线 , 直线 , 垂足分别为、 . 求证: .(2)、如图2,将(1)中的条件改为:在中, , 、、三点都在直线上,并且有 , 其中为任意锐角或钝角,那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.(3)、如图3,将(1)中的条件改为: , 、、三点都在直线上,且有 , 其中为任意锐角,那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.18. 阅读理解,自主探究:
(1)、如图1,在中, , , 直线经过点 , 直线 , 直线 , 垂足分别为、 . 求证: .(2)、如图2,将(1)中的条件改为:在中, , 、、三点都在直线上,并且有 , 其中为任意锐角或钝角,那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.(3)、如图3,将(1)中的条件改为: , 、、三点都在直线上,且有 , 其中为任意锐角,那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.18. 阅读理解,自主探究:“一线三垂直”模型是“一线三等角”模型的特殊情况,即三个等角角度为90°,于是有三组边相互垂直.所以称为“一线三垂直模型”.当模型中有一组对应边长相等时,则模型中必定存在全等三角形.
 (1)、问题解决:如图1,在等腰直角中, , , 过点C作直线 , 于D,于E,求证:;(2)、问题探究:如图2,在等腰直角中, , , 过点C作直线 , 于D,于E,cm,cm,求的长;(3)、拓展延伸:如图3,在平面直角坐标系中, , 为等腰直角三角形, , , 求B点坐标.19. 【模型呈现】
(1)、问题解决:如图1,在等腰直角中, , , 过点C作直线 , 于D,于E,求证:;(2)、问题探究:如图2,在等腰直角中, , , 过点C作直线 , 于D,于E,cm,cm,求的长;(3)、拓展延伸:如图3,在平面直角坐标系中, , 为等腰直角三角形, , , 求B点坐标.19. 【模型呈现】“数学区别于其它学科最主要的特征是抽象与推理”.“一线三等角”模型是几何世界中常见的模型之一,只要细心观察,你就可以从中找到全等三角形.
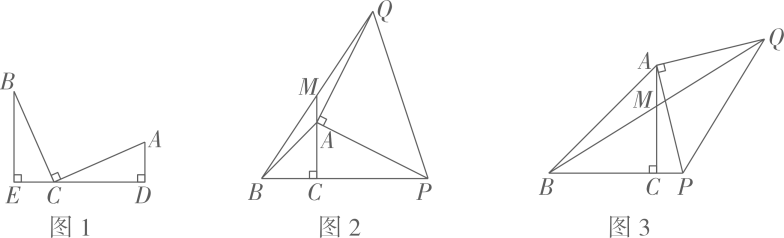 (1)、 【模型理解】如图1,已知,点C在线段DE上, , 若 , 则BE与CD的数量关系为 , BE, AD与DE的数量关系为;(2)、 【拓展延伸】在Rt中, , 分别以AC、AP为腰,在左侧作等腰直角三角形ABC,在右侧作等腰直角三角形APQ,其中 , ,
(1)、 【模型理解】如图1,已知,点C在线段DE上, , 若 , 则BE与CD的数量关系为 , BE, AD与DE的数量关系为;(2)、 【拓展延伸】在Rt中, , 分别以AC、AP为腰,在左侧作等腰直角三角形ABC,在右侧作等腰直角三角形APQ,其中 , ,① 如图2,连接BQ,当交线段CA的延长线于点M时,求证:;
② 如图3,连接BQ,当交线段CA于点M,且时,求BP的长.
20. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题∶
 (1)、如图1, , . 猜想 , , 之间的关系:(2)、如图2,将(1)中条件改为 , , 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点为上一点, , , , , 请直接写出的长.21. 【概念建构】
(1)、如图1, , . 猜想 , , 之间的关系:(2)、如图2,将(1)中条件改为 , , 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点为上一点, , , , , 请直接写出的长.21. 【概念建构】在中, , 直线MN经过点A , 于点D , 于点E . 如图1,当直线MN在外部时,称和是的“双外弦三角形”,如图2,当直线MN在内部时,称和是的“双内弦三角形”,依据“两角及其夹边分别相等的两个三角形全等”的基本事实,我们得到“双外弦三角形”和“双内弦三角形”都是全等三角形,即 .
 (1)、【概念应用】
(1)、【概念应用】如图3,在中,于点M , , E是BC边上的点, , , 连接AD , BD , 若 , 求BD的长.
小亮同学在阅读与理解【概念建构】的基础上,作于点N构造出如图4所示的“双内弦三角形”,并应用“双内弦三角形”是全等三角形的结论求出了BD . 请你依照小亮的解题思路,写出解答过程.
(2)、请你应用“双内弦三角形”和“双外弦三角形”都是全等三角形的结论或者按照自己的解题思路解答下列问题.如图5,在中, , D是AB边上一点, , DE交BC于点N , 延长EB , CD交于点F , 猜想DB , DF , CN之间的数量关系,并说明理由.
(3)、【学以数用】如图6, , 和是等腰直角三角形, , , 直接写出和的面积和.
(4)、【拓展延伸】如图7,在中, , 点D在AB边上,过B作交CD延长线于点E , 延长EB至点F , 连接CF , 使 , 连接AF交CD于点G , 若 , 直接写出的面积.