专题4 全等三角形翻折问题—浙教版数学八年级上册培优专训
试卷更新日期:2025-09-22 类型:复习试卷
一、选择题
-
1. 如图,圆圆做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRO的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A、C画一条射线AE,AE就是∠PRO的平分线:此角平分仪的画图原理是( )
 A、SSS B、SAS C、ASA D、AAS2. 如图,将沿AC对折,点与点重合,则全等的三角形有( )
A、SSS B、SAS C、ASA D、AAS2. 如图,将沿AC对折,点与点重合,则全等的三角形有( ) A、1对 B、2对 C、3对 D、4对
A、1对 B、2对 C、3对 D、4对二、填空题
-
3. 如图是一张三角形纸片,已知AC=6cm,BC=8cm.现将△ABC折叠,使点B与点A重合,折痕为DE,则△ACD的周长为.
 4. 如图,将图形沿直线AC对折,△ABC与△ADC重合,则△ABC≌.AB的对应边是 , BC的对应边是∠BCA的对应角是:
4. 如图,将图形沿直线AC对折,△ABC与△ADC重合,则△ABC≌.AB的对应边是 , BC的对应边是∠BCA的对应角是: 5. 如图,在四边形 ABCD中,AC平分∠BAD,过C作CE⊥AB于E,并且 , 那么,∠ABC+∠ADC的度数是.
5. 如图,在四边形 ABCD中,AC平分∠BAD,过C作CE⊥AB于E,并且 , 那么,∠ABC+∠ADC的度数是.
三、解答题
-
6. 如图,已知 , , 则 , 请说明理由.(填空)
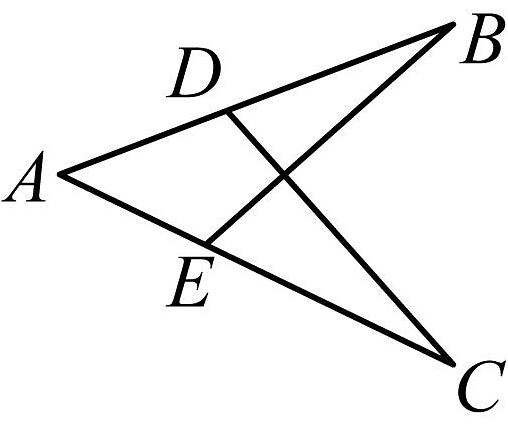
解:在和中,
∴(_________),
∴(_________).

