专题2 全等三角形判定专题练习—浙教版数学八年级上册培优专训

试卷更新日期：2025-09-22 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，把两根钢条 $A A^{'}$ ， $B B^{'}$ 的中点连在一起，可以做成一个测量工件内槽宽的卡钳．若求 $A B$ 的长，只需测量下列线段中的（）

A、 $A^{'} B^{'}$ B、 $O A^{'}$ C、 $O B^{'}$ D、OA

查看试题解析
2. 如图，已知 $∠ A B C = ∠ B A D$ ，添加下列条件还不能判定 $Δ A B C ≌ Δ B A D$ 的是（）

A、 $A C = B D$ B、 $∠ C A B = ∠ D B A$ C、 $∠ C = ∠ D$ D、 $B C = A D$

查看试题解析
3. 如图，图中的两个三角形全等，则 $∠ α$ 等于（）

A、 $71 °$ B、 $59 °$ C、 $49 °$ D、 $50 °$

查看试题解析
4. 如图，数学辅导书上的三角形被墨水污染了，根据所学知识可以在空白纸上画出一个完全一样的三角形，其依据是 ( )

A、SSS B、ASA C、AAS D、SAS

查看试题解析
5. 如图， $A C$ 与 $B D$ 相交于点 $O ， A B = D C ， ∠ A = ∠ D$ ，不添加辅助线，能直接判定 $△ A O B ≌ △ D O C$ 的依据是（）

A、 $SSS$ B、 $ASA$ C、 $AAS$ D、 $HL$

查看试题解析
6. 如图，是尺规作图中“画一个角等于已知角”的示意图，该作法运用了“全等三角形的对应角相等”这一性质，则判定图中两三角形全等的条件是（　　）

A、 $SSS$ B、 $ASA$ C、 $AAS$ D、 $SAS$

查看试题解析
7. 如图，点A在 $D E$ 上， $A C = E C$ ， $∠ 1 = ∠ 2 = ∠ 3$ ，则 $D E$ 等于（）

A、 $B C$ B、 $A B$ C、 $D C$ D、 $A E + A C$

查看试题解析
8. 如图，在 $Rt △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A B C$ 的角平分线交 $A C$ 于点D， $D E ⊥ B C$ 于点E，若 $△ A B C$ 与 $△ C D E$ 的周长分别为13和3，则 $A B$ 的长为（　　）

A、10 B、16 C、8 D、5

查看试题解析
9. 如图， $△ A B C$ 中， $∠ B = ∠ C$ ， $B D = C F$ ， $B E = C D$ ， $∠ E D F = a$ ，则下列结论正确的是（）

A、 $2 a + ∠ A = 180 °$ B、 $a + ∠ A = 90 °$ C、 $2 a + ∠ A = 90 °$ D、 $a + ∠ A = 180 °$

查看试题解析

二、填空题（每题3分，共21分）

10. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $B E ⊥ C E$ 于 $E$ ， $A D ⊥ C E$ 于 $D$ ， $A D = 5 cm$ ， $D E = 3 cm$ ， $B E =$ ．

查看试题解析
11. 如图，点B，F，E，C在同一直线上， $A B ∥ C D$ ，且 $A B = C D$ ，要使 $△ A B E ≌ △ D C F$ ，则可以添加的条件是．（只需填上一个即可）

查看试题解析
12. 如图，在 $△ A B C$ 中，已知 $A D$ 平分 $∠ B A C$ ，且 $A D ⊥ B D$ 于点D， $△ A D C$ 的面积是8，则 $△ A B C$ 的面积是．

查看试题解析
13. 如图，已知 $B E ⊥ A D$ ， $C F ⊥ A D$ ，且 $B E = C F$ ，那么 $A D$ 是 $△ A B C$ 的．（填“中线”或“角平分线”）

查看试题解析
14. 如图，在 $△ A B C$ ， $△ A D E$ 中， $∠ B A C = ∠ D A E = 90 °$ ， $A B = A C$ ， $A D = A E$ ， C，D，E三点在同一直线上，连接 $B D ， B E$ ，以下四个结论

① $B D = C E$ ；② $∠ A C E + ∠ D B C = 90 °$ ；
③ $B D ⊥ C E$ ；④ $∠ B A E + ∠ D A C = 180 °$ ．
其中结论正确的是．（把正确结论的序号填在横线上）．

查看试题解析
15. 如图，在四边形 $A B C D$ 中，对角线 $A C ⊥ B D$ ， $F$ 为 $C D$ 上一点，连结 $A F$ 交 $B D$ 于点 $E$ ， $A F ⊥ A B$ ，已知 $∠ B A G = ∠ A B C = 45 °$ ，且 $B C + A G = 10 \sqrt{2}$ ．

(1)、则 $A B$ 的长是；

(2)、若 $A E = 2 E F$ ，且 $∠ A G D + ∠ B C D = 180 °$ ，则 $A F =$ ．

查看试题解析

三、解答题（共7题，共69分）

16. 如图，已知点A，B以及直线l.

(1)、用直尺和圆规作线段AB的垂直平分线，交直线l于点P.

(2)、在(1)所作的图中，M，N是直线l上的两点.若AM=PN，BN=PM.求证：∠MAP=∠NPB.

查看试题解析
17. 图1，图2都是 $4 \times 4$ 的正方形网格，每个小正方形的顶点称为格点．三个顶点均在格点上的三角形称为格点三角形．在给定的网格中，按下列要求用无刻度的直尺画出相应的格点三角形．

(1)、在图1中画出以 $A B$ 为底的等腰三角形 $A B C$ ；

(2)、在图2中画出所有与 $△ D E F$ 全等（不包含 $△ D E F$ ）的 $△ E F G$ ．

查看试题解析
18. 小明将下列题目梳理到自己的错题本中，题目为“如图，点 $F$ ， $B$ ， $C$ ， $E$ 在同一条直线上， $A E ∥ D F$ ，且 $B F = C E$ ， $∠ A = ∠ D$ ．求证： $A B = C D$ ． ”，请你帮他完成题目的梳理过程．
题目来源
第一章书本例题
图形呈现
关键已知
① $A E / / D F$ ② $B F = C E$ ③ $∠ A = ∠ D$
解题过程

查看试题解析
19. 已知： $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点 $E$ 为 $△ A B C$ 内一点，连接 $A E$ ， $C E$ ， $C E ⊥ A E$ ，过点 $B$ 作 $B D ⊥ A E$ ，交 $A E$ 的延长线于点 $D$ ．

(1)、如图 $1$ ，求证： $B D = A E$ ；

(2)、如图 $2$ ，点 $H$ 为 $B C$ 的中点，分别连接 $E H$ ， $D H$ ，求 $∠ E D H$ 的度数．

查看试题解析
20. 如图， A B∥C D ， AC = DC ，____，求证： $△ A B C ≅ △ C E D .$

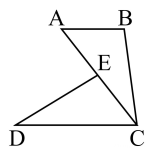(1)、请从①∠AED=∠BCD，②DE=BC，③DC-AE=AB 中选择一个适当的条件填入横线中，使命题成立.你的选择是(只需填一个序号即可)；

(2)、根据(1)中的选择给出证明.

查看试题解析
21. （1）如图 $1$ ，在 $△ A B C$ 与 $△ A D E$ 中， $A B = A C$ ， $A D = A E$ ， $∠ B A C = ∠ D A E = 90 °$ ，求证： $△ A E C ≌ △ A D B$ ；
（2）如图 $2$ ，在 $△ A B C$ 与 $△ A D E$ 中， $A B = A C$ ， $A D = A E$ ， $∠ B A C = ∠ D A E = 90 °$ ，点 $B$ ， $D$ ， $E$ 在一条直线上， $A C$ 与 $B E$ 交于点 $F$ ， $F$ 为 $A C$ 中点，求 $∠ B E C$ 的度数．

查看试题解析
22. 如图

(1)、【探究与发现】如图1， $A D$ 是 $△ A B C$ 的中线，延长 $A D$ 至点E，使 $E D = A D$ ，连接 $B E$ ，写出图中全等的两个三角形．

(2)、【理解与应用】填空：如图2， $E P$ 是 $△ D E F$ 的中线，若 $E F = 5$ ， $D E = 3$ ，设 $E P = x$ ，则x的取值范围是．

(3)、已知：如图3， $A D$ 是 $△ A B C$ 的中线， $∠ B A C = ∠ A C B$ ，点Q在 $B C$ 的延长线上， $Q C = B C$ ，求证： $A Q = 2 A D$ ．

查看试题解析

题目来源	第一章书本例题	图形呈现
关键已知	① $A E / / D F$ ② $B F = C E$ ③ $∠ A = ∠ D$
解题过程