专题1 全等三角形判定专题手拉手模型—浙教版数学八年级上册培优专训
试卷更新日期:2025-09-22 类型:复习试卷
一、选择题
-
1. 如图,已知 , 则的度数为( )
 A、 B、 C、 D、2. 如图,∠1=∠2,AB=EB,CB=DB,则△ABD≌△EBC时,运用的判定定理是()
A、 B、 C、 D、2. 如图,∠1=∠2,AB=EB,CB=DB,则△ABD≌△EBC时,运用的判定定理是()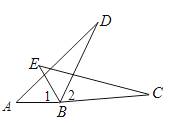 A、SSS B、ASA C、AAS D、SAS3. 如图,和都是等边三角形,下列结论:①;②平分;③;④;其中正确的有( )个
A、SSS B、ASA C、AAS D、SAS3. 如图,和都是等边三角形,下列结论:①;②平分;③;④;其中正确的有( )个 A、2 B、3 C、4 D、14. 如图, , 连接 , 点 恰好在 上, 则 ( )
A、2 B、3 C、4 D、14. 如图, , 连接 , 点 恰好在 上, 则 ( ) A、 B、 C、 D、无法计算5. 如图, , 连接 , 点 D 恰好在上, 则( )
A、 B、 C、 D、无法计算5. 如图, , 连接 , 点 D 恰好在上, 则( ) A、60 ° B、59 ° C、61 ° D、无法计算6. 如图,A、C、B三点在同一条直线上,和都是等边三角形,分别与交于点M、N,有如下结论:①;②;③;④是等边三角形;其中,正确结论的个数是( )
A、60 ° B、59 ° C、61 ° D、无法计算6. 如图,A、C、B三点在同一条直线上,和都是等边三角形,分别与交于点M、N,有如下结论:①;②;③;④是等边三角形;其中,正确结论的个数是( )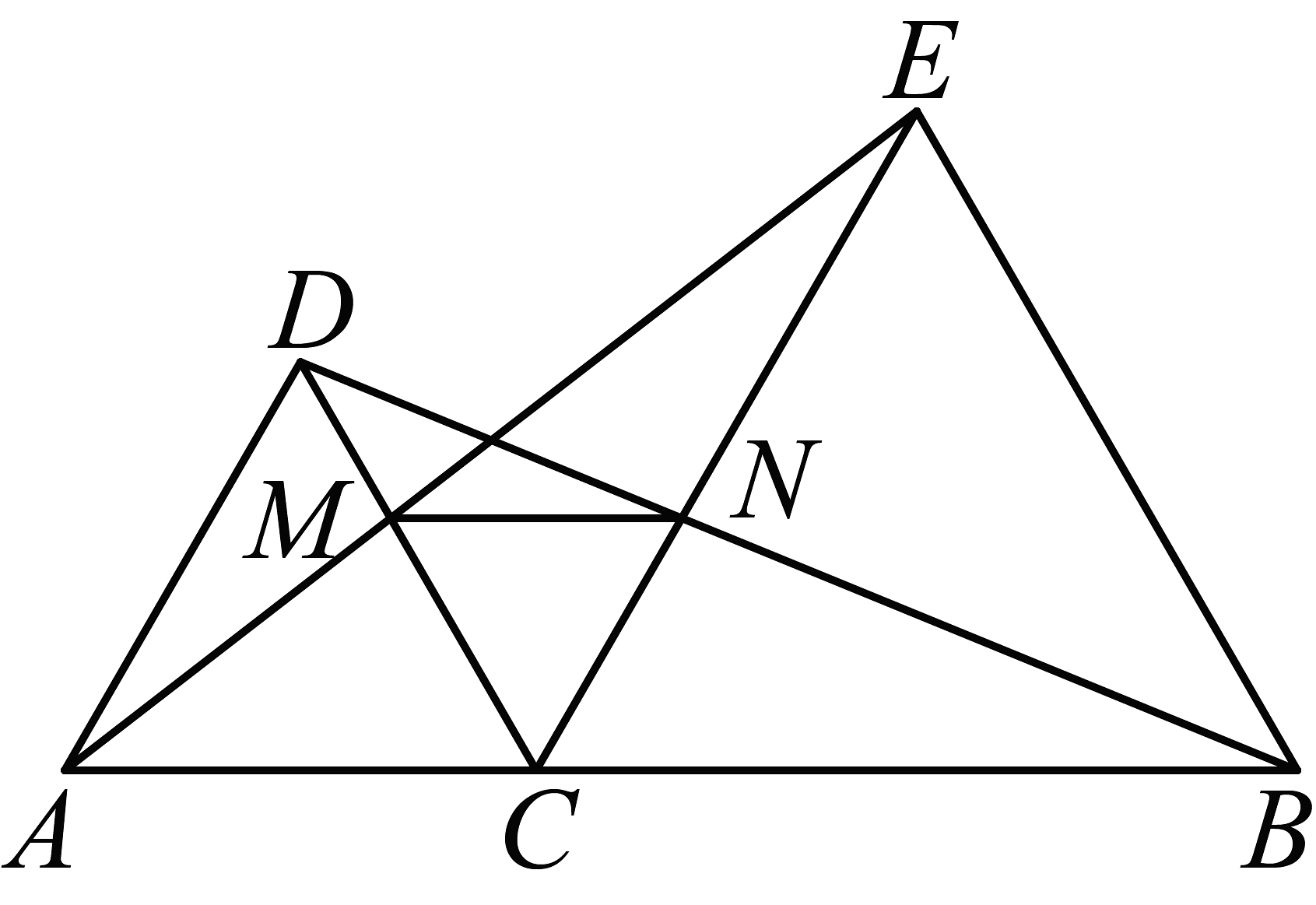 A、1个 B、2个 C、3个 D、4个7. 如图,在和中, , , , 过作 , 垂足为 , 交的延长线于点 , 连接 . 四边形的面积为64, . 则的长是( )
A、1个 B、2个 C、3个 D、4个7. 如图,在和中, , , , 过作 , 垂足为 , 交的延长线于点 , 连接 . 四边形的面积为64, . 则的长是( ) A、8 B、 C、 D、68. 如图,在 和 中, ,连接 交于 点 ,连接 . 下列结论: ; ; 平分 ; 平分 . 其中正确的个数为( )
A、8 B、 C、 D、68. 如图,在 和 中, ,连接 交于 点 ,连接 . 下列结论: ; ; 平分 ; 平分 . 其中正确的个数为( ) A、1 B、2 C、3 D、49. 如图,在△OAB和△OCD中,OA=OB , OC=OD,OA>OC , ∠AOB=∠COD=40°,连接AC,BD交于点M , 连接OM . 下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC . 其中正确的个数为( )
A、1 B、2 C、3 D、49. 如图,在△OAB和△OCD中,OA=OB , OC=OD,OA>OC , ∠AOB=∠COD=40°,连接AC,BD交于点M , 连接OM . 下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC . 其中正确的个数为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
10. 如图,AB=AC,AD=AE,∠BAC=∠DAE.若∠1=25°,∠2=30°,则∠3=.
 11. 在 中, , 点 是直线 上一点(不与 重合), 以 为一边在 的右侧作 , 使 , 连接 .
11. 在 中, , 点 是直线 上一点(不与 重合), 以 为一边在 的右侧作 , 使 , 连接 . (1)、 如图 1, 当点 在线段 上, 如果 , 则 度;(2)、点 在直线 上移动,若 。则 之间的数量关系为。12. 在中, , 点D是直线上一点(不与B、C重合),以为一边在=的右侧作 , 使 , , 连接 .
(1)、 如图 1, 当点 在线段 上, 如果 , 则 度;(2)、点 在直线 上移动,若 。则 之间的数量关系为。12. 在中, , 点D是直线上一点(不与B、C重合),以为一边在=的右侧作 , 使 , , 连接 .
(1)如图1,当点在线段上,如果 , 则度;
(2)点D在直线上移动,若 , . 则α,β之间的数量关系为 .
13. 如图 ,C 为线段 上一动点 (不与点 重合), 在 同侧分别作等边三角形 和等边三角形 , 连结 , 交于点 , 则 . 14. 如图, C 是线段 上一点, 分别以 为边在 同侧作等边三角形 和等边三角形 , 连结 交 于点 , 连结 交 于点 . 若 , 则 .
14. 如图, C 是线段 上一点, 分别以 为边在 同侧作等边三角形 和等边三角形 , 连结 交 于点 , 连结 交 于点 . 若 , 则 . 15. 小王在探究等边三角形“手拉手”问题,得出以下四个结论.
15. 小王在探究等边三角形“手拉手”问题,得出以下四个结论.如图 , 已知 , 均为等边三角形,点在线段上,且不与点、点重合,连接 , 则;
已知条件同 , 则;
如图 , 已知 , 均为等边三角形,点在内部,连接、 , 则、、三点共线;
如图 , 已知为等边三角形,点在外,并且与点位于线段的异侧,连接、 . 若 , 则 .
以上结论正确的是 .

三、解答题
-
16. 如图,在中, , D是内一点,连接 , 将线段绕点C逆时针旋转到 , 使 , 连接 .
 (1)、求证: .(2)、当时,求与的度数和.17. 如图, ,点 在 上.
(1)、求证: .(2)、当时,求与的度数和.17. 如图, ,点 在 上. (1)、求证: ;(2)、若 平分 ,求 的度数.18. 在中, , 点D是直线上一点(不与B,C重合),以为一边在的右侧作 , 使 , , 连接 .
(1)、求证: ;(2)、若 平分 ,求 的度数.18. 在中, , 点D是直线上一点(不与B,C重合),以为一边在的右侧作 , 使 , , 连接 . (1)、如图1,当点D在线段上时,如果 , 则 °.(2)、设 .
(1)、如图1,当点D在线段上时,如果 , 则 °.(2)、设 .①如图2,当点D在线段上移动时,α、β之间有怎样的数量关系?请说明理由.
②当点D在直线上移动时,α、β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论.
19. 在和中, , , , 点D是直线上的一动点(点D不与B,C重合),连接 . (1)、在图1中,当点D在边上时,求证:;(2)、在图2中,当点D在边的延长线上时,结论是否还成立?若不成立,请猜想 , , 之间存在的数量关系,并说明理由;(3)、在图3中,当点D在边的反向延长线上时,不需写证明过程,直接写出 , , 之间存在的数量关系及直线与直线的位置关系.
(1)、在图1中,当点D在边上时,求证:;(2)、在图2中,当点D在边的延长线上时,结论是否还成立?若不成立,请猜想 , , 之间存在的数量关系,并说明理由;(3)、在图3中,当点D在边的反向延长线上时,不需写证明过程,直接写出 , , 之间存在的数量关系及直线与直线的位置关系.