鲁教版(五四制)数学九年级上学期期中仿真模拟试卷一(1-3章)
试卷更新日期:2025-09-18 类型:期中考试
一、选择题:本题共10小题,每小题3分,共30分。每小题只有一个选项符合题目要求.
-
1. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、2. 若点、在反比例函数图像上,则、大小关系是( )A、 B、 C、 D、3. 如图所示,点A,B,C对应的刻度分别为1,3,5,将线段绕点C按顺时针方向旋转,当点A首次落在矩形的边上时,记为点 , 则此时线段扫过的图形的面积为( )
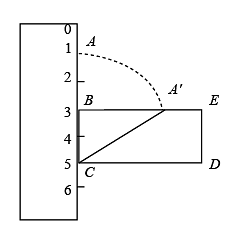 A、 B、6 C、 D、4. 在中, , 则( )A、 B、 C、 D、5. 已知抛物线经过和两点,则n的值为( )A、 B、 C、2 D、46. 一次函数的图象如图所示,则二次函数的图象大致是( )
A、 B、6 C、 D、4. 在中, , 则( )A、 B、 C、 D、5. 已知抛物线经过和两点,则n的值为( )A、 B、 C、2 D、46. 一次函数的图象如图所示,则二次函数的图象大致是( )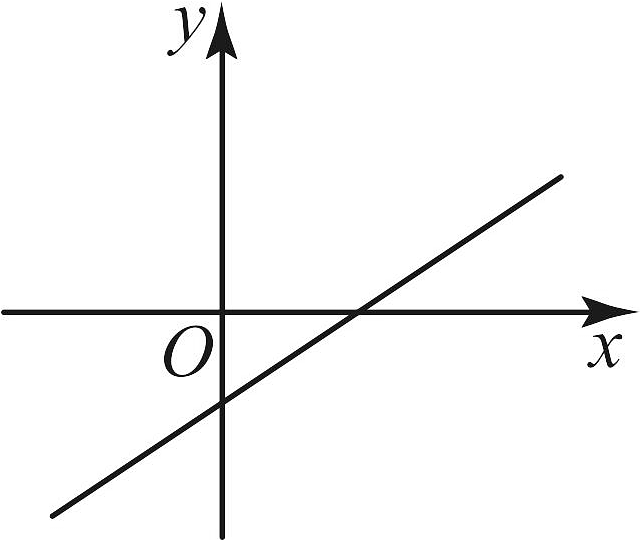 A、
A、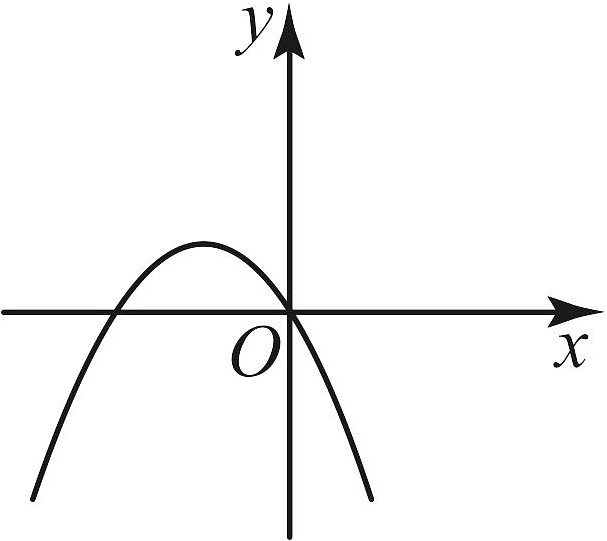 B、
B、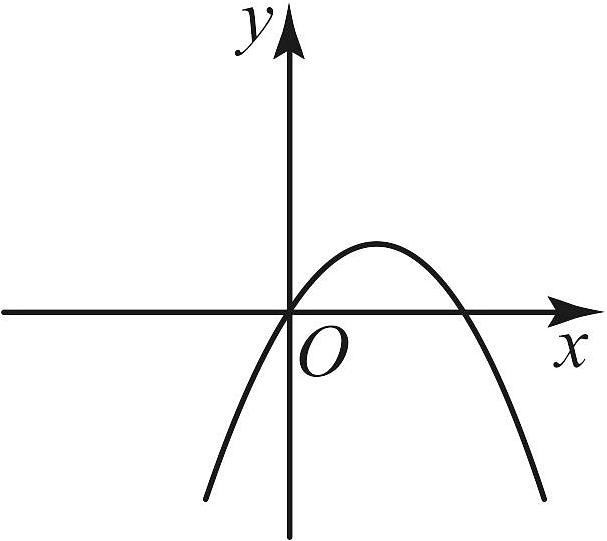 C、
C、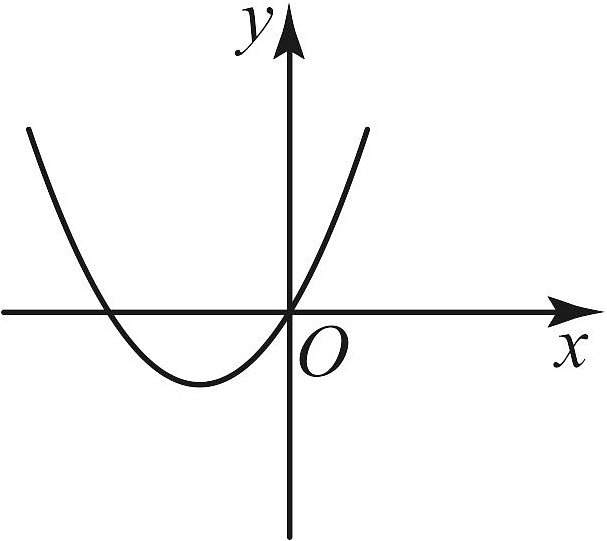 D、
D、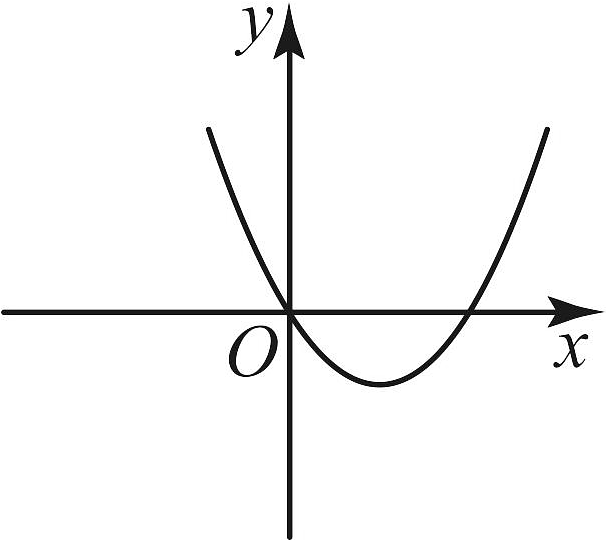 7. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点,当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF//BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
7. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点,当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF//BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)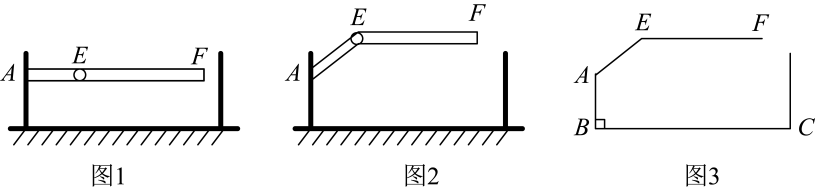 A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,矩形ABCD的面积为 , A点的坐标为(2,1),轴,轴,若反比例函数的图像过点B、D,则k的值为( )
8. 如图,矩形ABCD的面积为 , A点的坐标为(2,1),轴,轴,若反比例函数的图像过点B、D,则k的值为( )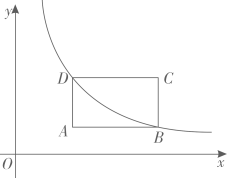 A、 B、 C、5 D、9. 如图,点、在双曲线上,直线分别与轴、轴交于点、 , 与双曲线交于点 , 连接 , 若 , , 则的值为( )
A、 B、 C、5 D、9. 如图,点、在双曲线上,直线分别与轴、轴交于点、 , 与双曲线交于点 , 连接 , 若 , , 则的值为( )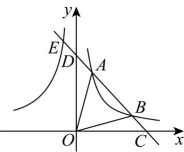 A、 B、 C、 D、10. 如图,抛物线的顶点A的坐标为 , 与x轴的一个交点的横坐标位于0和之间,则以下结论:①;②;③若抛物线经过点 , , 则;④若关于x的一元二次方程有实数根,则 . 其中正确的个数为( )
A、 B、 C、 D、10. 如图,抛物线的顶点A的坐标为 , 与x轴的一个交点的横坐标位于0和之间,则以下结论:①;②;③若抛物线经过点 , , 则;④若关于x的一元二次方程有实数根,则 . 其中正确的个数为( )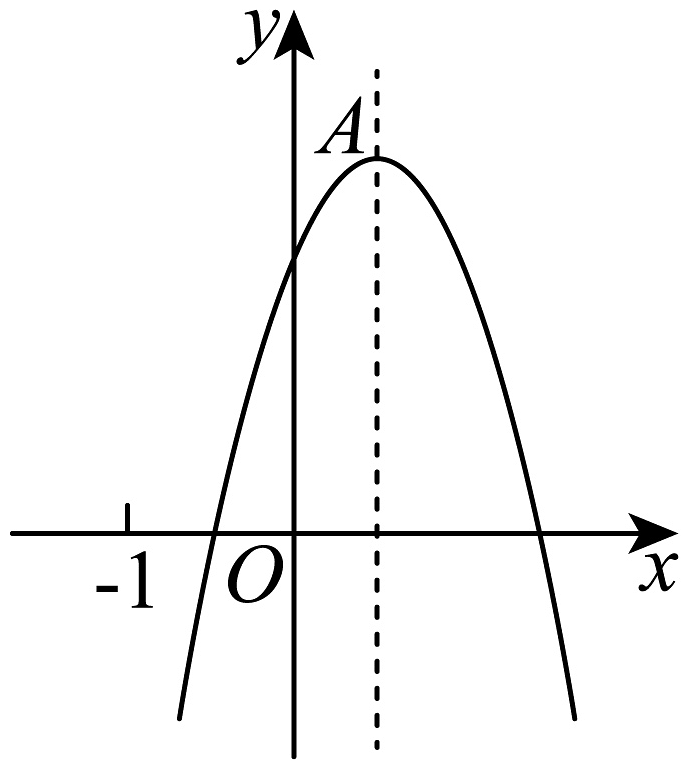 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题:本题共5小题,每小题3分,共15分.
-
11. .12. 关于的方程无解,则反比例函数的图象在第象限.13. 如图,正方形ABCD的边长为2,点B与原点O重合,与反比例函数的图象交于E、F两点,若的面积为 , 则k的值
 14. 《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长 , “矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 .
14. 《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积(弦矢+矢),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长 , “矢”等于半径长与圆心到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为2,则的值为 . 15. 如图,△DEF 的三个顶点分别在等边 三 角 形 ABC 的三 条 边 上,BC =4, 则 DF 长度的最小值是.
15. 如图,△DEF 的三个顶点分别在等边 三 角 形 ABC 的三 条 边 上,BC =4, 则 DF 长度的最小值是.
三、解答题:本题共8小题,共75分.解答应写出文字说明、证明过程或演算步骤.
-
16. 已知二次函数 , 当时,;当时, .(1)、求这个二次函数表达式及该函数顶点坐标;(2)、此函数图象与轴交于点 , (在的左边),与轴交于点 , 求点 , , 的坐标.17. 中国古代运用“土圭之法”判别四季.夏至时日影最短,冬至时日影最长,春分和秋分时日影长度等于夏至和冬至日影长度的平均数.某地学生运用此法进行实践探索,如图,在示意图中,产生日影的杆子垂直于地面,长8尺.在夏至时,杆子在太阳光线照射下产生的日影为;在冬至时,杆子在太阳光线照射下产生的日影为 . 已知 , .
 (1)、求冬至时日影的长度;(2)、求春分和秋分时日影长度(结果精确到0.1尺).(参考数据: , , , , , )18. 如图,反比例函数的图象与一次函数的图象交于点、点 .
(1)、求冬至时日影的长度;(2)、求春分和秋分时日影长度(结果精确到0.1尺).(参考数据: , , , , , )18. 如图,反比例函数的图象与一次函数的图象交于点、点 .
(1)求一次函数和反比例函数的解析式;
(2)求的面积;
(3)直接写出一次函数值大于反比例函数值的自变量的取值范围.
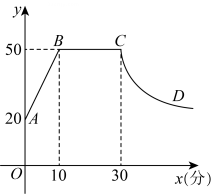
19. 心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中、分别为线段,为双曲线的一部分).(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知——自主探索,合作交流——总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40,请问这样的课堂学习安排是否合理?并说明理由.
 20. 如图是某品牌篮球架及其示意图,立柱垂直地面 , 支架与交于点A,支架交于点G,支架平行地面 , 篮筐与支架在同一直线上,米,米, . (参考数据: , , )
20. 如图是某品牌篮球架及其示意图,立柱垂直地面 , 支架与交于点A,支架交于点G,支架平行地面 , 篮筐与支架在同一直线上,米,米, . (参考数据: , , ) (1)、求的度数.(2)、工人准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3米处,那么他能挂上篮网吗?请通过计算说明理由.21. 已知二次函数 ( 为常数)的图象经过点 ,对称轴是直线 。
(1)、求的度数.(2)、工人准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3米处,那么他能挂上篮网吗?请通过计算说明理由.21. 已知二次函数 ( 为常数)的图象经过点 ,对称轴是直线 。
(1)、求此二次函数的表达式。(2)、求二次函数 的最大值。(3)、当 时,二次函数 的最大值与最小值的差为 ,求 的取值范围。22. 如图,在平面直角坐标系中, 直线分别与y轴、x轴相交于点 A, , 过点A的直线与双曲线交于C,D两点(点C在点D的右侧). (1)、求a的值及线段的长;(2)、过点C作轴于点E,过点D作轴于点F,若 , 求k的值及的面积;(3)、将直线沿y轴翻折得到新直线,新直线与x轴相交于点G,再将的图象沿着直线翻折,翻折后的图象交直线于点M,N(点M在点N左侧),当与相似时,求k的值.23. 定义:在平面直角坐标系中,到两个坐标轴的距离都小于或等于的点叫“阶近轴点”,所有的“阶近轴点”组成的图形记为图形 . 如图所示,所有的“1阶近轴点”组成的图形是以坐标原点为中心,2为边长的正方形区域.
(1)、求a的值及线段的长;(2)、过点C作轴于点E,过点D作轴于点F,若 , 求k的值及的面积;(3)、将直线沿y轴翻折得到新直线,新直线与x轴相交于点G,再将的图象沿着直线翻折,翻折后的图象交直线于点M,N(点M在点N左侧),当与相似时,求k的值.23. 定义:在平面直角坐标系中,到两个坐标轴的距离都小于或等于的点叫“阶近轴点”,所有的“阶近轴点”组成的图形记为图形 . 如图所示,所有的“1阶近轴点”组成的图形是以坐标原点为中心,2为边长的正方形区域.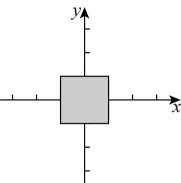 (1)、下列函数图象上存在“1阶近轴点”的是;
(1)、下列函数图象上存在“1阶近轴点”的是;①;②;③ .
(2)、若一次函数的图像上存在“3阶近轴点”,求实数的取值范围;(3)、特别地,当点在图形上,且横坐标是纵坐标的倍时,称点是图形的“阶完美点”,若二次函数的图像上有且只有一个“2阶完美点”,求实数的取值范围.