鲁教版（五四制）数学九年级上学期期中仿真模拟试卷二（1-4章）

试卷更新日期：2025-09-18 类型：期中考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。每小题只有一个选项符合题目要求.

1. 如图是由立方体叠成的立体图形，从正面看，得到的主视图为（）

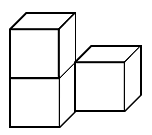A、 B、 C、 D、

查看试题解析
2. 如果当 $x > 0$ 时，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的函数值随x的增大而增大，那么一次函数 $y = \frac{1}{3} k x - 2 k$ 的图象经过（）

A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限

查看试题解析
3. 如图，在 $△ A B C$ 中，若 $∠ B = 9 0^{°}, A B = 3, B C = 4$ ，则 $t a n A =$ （）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
4. 如图，在平面直角坐标系中，反比例函数 $y_{1} = \frac{2}{x}$ 的图像与一次函数 $y_{2} = k x + b$ 的图像交于 $A$ 、 $B$ 两点．若 $y_{1} < y_{2}$ ，则 $x$ 的取值范围是（　　）

A、 $1 < x < 3$ B、 $x < 0$ 或 $1 < x < 3$ C、 $0 < x < 1$ D、 $x > 3$ 或 $0 < x < 1$

查看试题解析
5. 如图，在 $5 \times 5$ 的正方形网格中，每个小正方形的边长都是1， $△ A B C$ 的顶点都在正方形顶点上，那么 $\cos ∠ A C B$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
6. 二次函数 $y = {(x + 2)}^{2} - 3$ 的图象的顶点坐标是（）

A、 $(- 2, 3)$ B、 $(2, 3)$ C、 $(2, - 3)$ D、 $(- 2, - 3)$

查看试题解析
7. 如图所示，该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
8. 在同一平面直角坐标系中，函数 $y = a x + a$ 和 $y = - a x^{2} + 3 x + 3$ （a是常数，且 $a \neq 0$ ）的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
9. 抛物线 $y = {(x - 1)}^{2} + k$ 经过 $(- 2, y_{1})$ ， $(3, y_{2})$ 两点，则 $y_{1} 、 y_{2}$ 的大小关系正确的是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、不能确定

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，下列结论：① $a > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $4 a + b = 0$ ；④不等式 $a x^{2} + (b - 1) x + c < 0$ 的解集为 $1 < x < 3$ ．正确的结论个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题：本题共5小题，每小题3分，共15分.

11. 若点 $A (- 3 ， y_{1})$ ， $B (- 1 ， y_{2})$ 都在反比例函数 $y = \frac{6}{x}$ 的图象上，则 $y_{1}$ $y_{2}$ （填“>”或“<”）.

查看试题解析
12. 如图，在平面直角坐标系 $x O y$ 中，矩形 $O A B C$ 的两边 $O C$ 、 $O A$ 分别在 $x$ 轴、 $y$ 轴的正半轴上，反比例函数 $y = \frac{k}{x} (x > 0)$ 与 $A B$ 相交于点 $D$ ，与 $B C$ 相交于点 $E$ ，若 $B E = 4 E C$ ，且 $△ O D E$ 的面积是12，则 $k$ 的值为．

查看试题解析
13. 在平面直角坐标系中，将点 $A (3, \sqrt{3})$ 绕点O逆时针旋转 $150 °$ ，得到点 $A^{'}$ ，则点 $A^{'}$ 的坐标为．

查看试题解析
14. 古希腊数学家泰勒斯曾利用立杆测影的方法，在金字塔塔顶A的影子 $A^{'}$ 处直立一根木杆 $B C$ ，借助太阳光测金字塔的高度．如图所示，木杆 $B C$ 长2米．它的影长 $B C$ 是3米，同一时刻测得 $O A^{'}$ 是201米，则金字塔的高度 $A O$ 是米．

查看试题解析
15. 如图，在平面直角坐标系中，A、B两点在反比例函数 $y = \frac{k}{x} (k > 0, x > 0)$ 的图象上，延长AB交 $x$ 轴于点 $C$ ，且 $A B = B C, D$ 是第二象限一点，且 $D O / / A B$ ，若 $△ A D C$ 的面积是12，则 $k$ 的值为．

查看试题解析

三、解答题：本题共8小题，共75分.解答应写出文字说明、证明过程或演算步骤.

16. 已知二次函数 $y = - x^{2} + b x + c$ 经过点 $A （ 3 ， 0 ）$ 与 $B （ 0 ， 3 ）$ ．

(1)、求b，c的值．

(2)、求该二次函数图象的顶点坐标．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点D， $A B = 10$ ， $s i n B = \frac{3}{5}$ .

(1)、求AD的长；

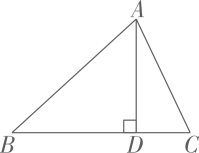(2)、若 $B D = 2 C D$ ，求 $t a n C$ 的值.

查看试题解析
18. 如图

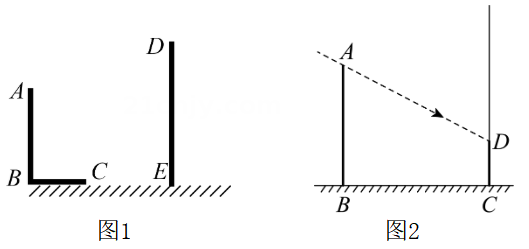(1)、【基础解答】如图1，AB和DE是直立在地面上的两根立柱，AB=6m，某一时刻AB在阳光下的投影BC=2m，DE在阳光下的投影长为3m.根据题中信息，求立柱DE的长.

(2)、【拓展拔高】如图2，古树AB在阳光照射下，影子的一部分照射在地面，即BC=4m，还有一部分影子在建筑物的墙上，墙上的影高CD为1m，同一时刻，竖直于地面上的1m长的竹竿，影长为2m，求这棵古树A8的高.

查看试题解析
19. 如图，一次函数 $y = a x + b$ 的图像与反比例函数 $y = \frac{k}{x}$ 的图像交于 $C (1, 4)$ ， $D (4, m)$ 两点，与坐标轴交于 $A$ 、 $B$ 两点，连接 $O C$ ， $O D$ ．

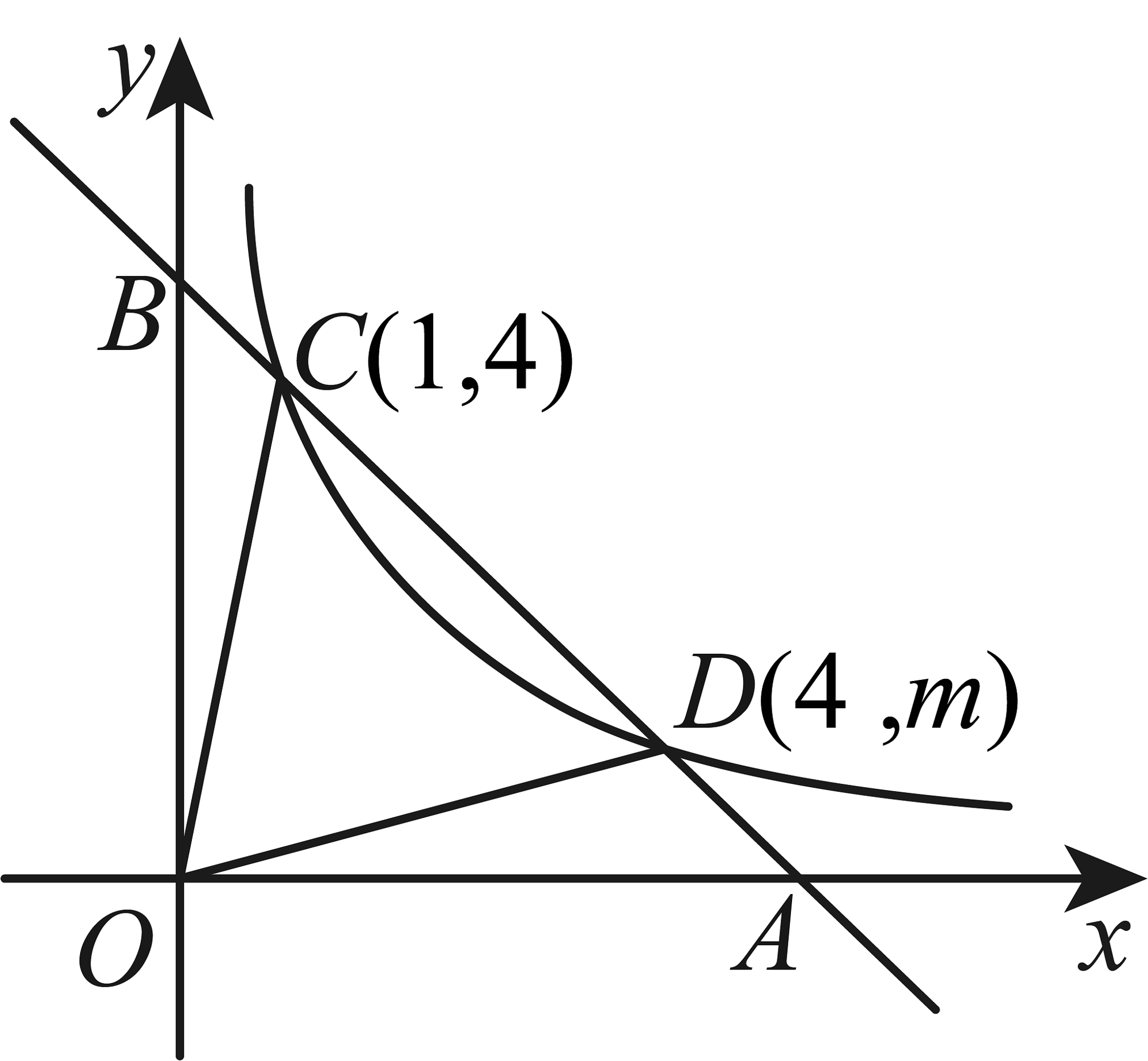(1)、求一次函数与反比例函数的表达式；

(2)、将直线 $A B$ 向下平移多少个单位长度，直线与反比例函数图象只有一个交点？

查看试题解析
20. 黄鹤楼是武汉市著名的旅游景点，享有“天下江山第一楼”的美誉．在一次综合实践活动中，某数学小组用无人机测量黄鹤楼 $A B$ 的高度，具体过程如下：如图，将无人机垂直上升至距水平地面 $102 m$ 的 $C$ 处，测得黄鹤楼顶端 $A$ 的俯角为 $45 °$ ，底端 $B$ 的俯角为 $63 °$ ，求黄鹤楼的高度（参考数据： $\tan 63 ° \approx 2$ ）．

查看试题解析
21. 如图，直线AB：y=k₁x+b与x轴、y轴分别相交于点A（1，0）和点B（0，2），以线段AB为边在第一象限作正方形ABCD．
（1）求直线AB的解析式；
（2）求点D的坐标；
（3）若双曲线 $y = \frac{k_{2}}{x}$ （k＞0）与正方形的边CD始终有一个交点，求k₂的取值范围．

查看试题解析
22. 如图，点A，B在x轴上，以AB为边的正方形ABCD在x轴上方，点C的坐标为（1，4），反比例函数 $y = \frac{k}{x}$ （k≠0）的图象经过CD的中点E，F是AD上的一个动点，将△DEF沿EF所在直线折叠得到△GEF．
（1）求反比例函数 $y = \frac{k}{x}$ （k≠0）的表达式；
（2）若点G落在y轴上，求线段OG的长及点F的坐标．

查看试题解析

23. 如何拟定运动员拍照记录的方案？

素材1

图1是单板滑雪运动员从大跳台滑雪场地滑出的场景，图2是跳台滑雪场地的横截面示意图． $A C$ 垂直于水平底面 $B C$ ，点D到A之间的滑道呈抛物线型．已知 $A C = 3 m$ ， $B C = 4 m$ ，且点B处于跳台滑道的最低处．

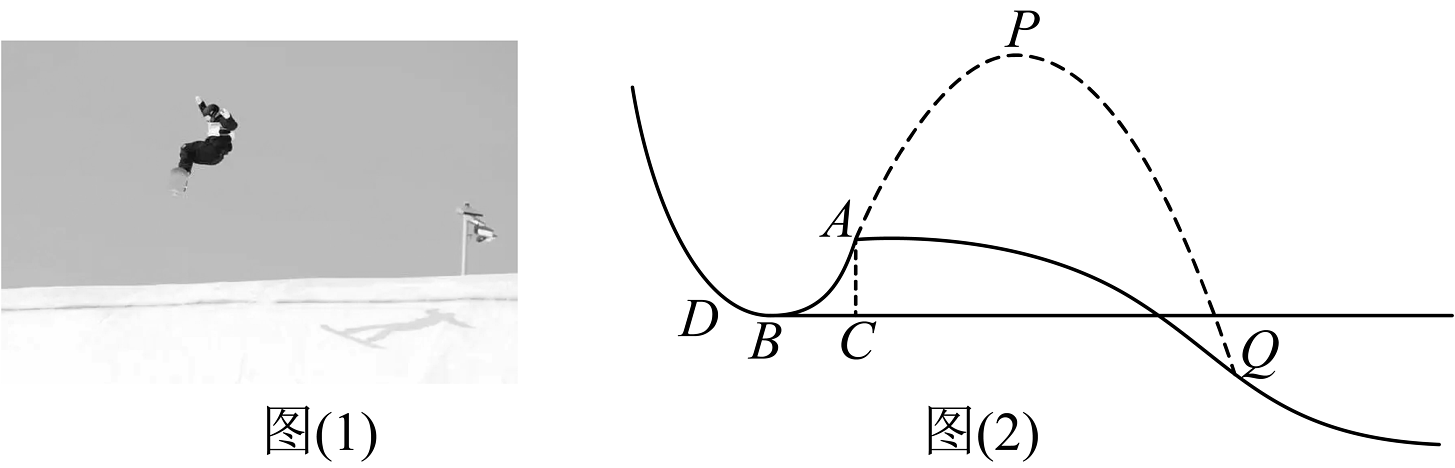
素材2

如图3，某运动员从点A滑出后的路径满足以下条件：

①运动员滑出路径与D、A之间的抛物线形状相同．

②该运动员在底面 $B C$ 上方竖直距离 $9.75 m$ 处达到最高点P．

③落点Q在底面 $B C$ 下方竖直距离 $2.25 m$ ．

素材3

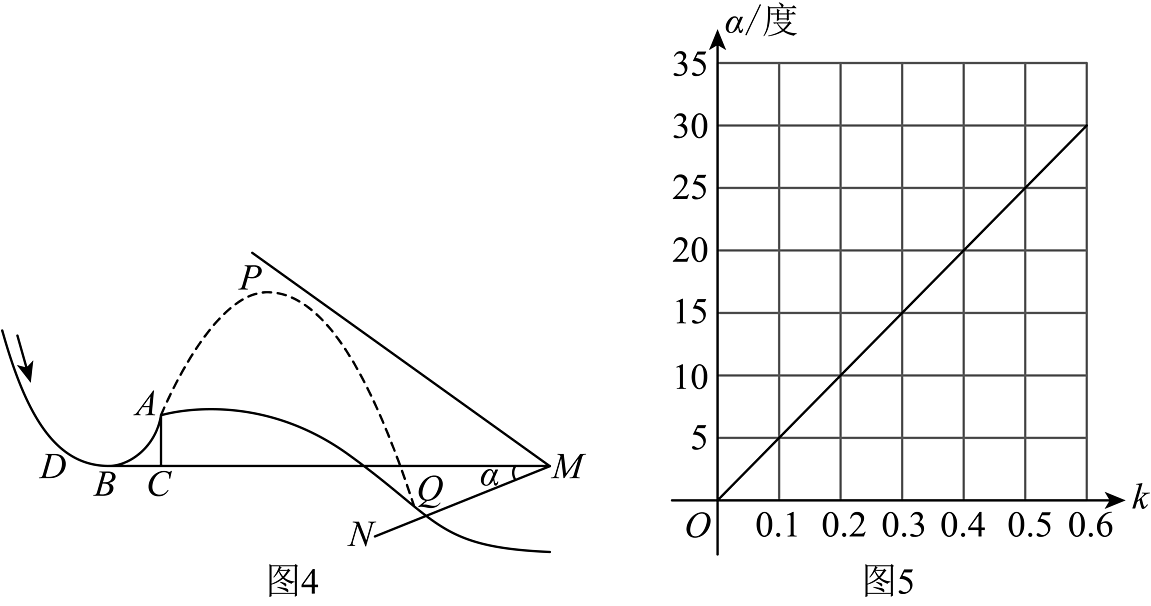
高速摄像机能高度还原运动员的精彩瞬间，如图4，有一台摄像机M进行跟踪拍摄：

①它与点B位于同一高度，且与点B距离 $25.5 m$ ；

②运动过程需在摄像头视角范围内才能记录，记摄像头的俯角为α；

③在平面直角坐标系中，设射线 $M N$ 的解析式为 $y = k x + b (k \neq 0)$ ，其比

例系数k和俯角α的函数关系如图5所示．

问题解决

任务1	确定D、A之间滑道的形状	在图2中建立适当的平面直角坐标系，求滑道所在抛物线的函数表达式．
任务2	确定运动员达到最高点的位置	在同一平面直角坐标系中，求运动员到达最高处时与点A的水平距离．
任务3	确定拍摄俯角α	若要求运动员的落点Q必须在摄像机M的视角范围内，则俯角α至少多少度（精确到个位）？

查看试题解析