鲁教版（五四制）数学八年级上学期期中仿真模拟试卷二（范围：1-3章）

试卷更新日期：2025-09-18 类型：期中考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。每小题只有一个选项符合题目要求.

1. 某班对一小组7名男生一分钟垫排球的个数进行统计，整理数据后发现26，27，2，31，32，38，39中第三个数的个位数字被涂污看不消楚了，则下列统计量中与被涂污数字无关的是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
2. 分式 $\frac{x^{2} - 4}{x - 2}$ 的值为0，则（）

A、x＝0 B、x＝﹣2 C、x＝2 D、x＝±2

查看试题解析
3. 某射击爱好者的10次射击成绩（单位：环）依次为：7，9，10，8，9，8，10，10，9，10，则下列结论正确的是（　　）

A、平均数是9.5 B、中位数是9 C、众数是9 D、方差是2

查看试题解析
4. 根据分式的性质，可以将分式 $M = \frac{m^{2} - 2 m + 1}{m^{2} - 1}$ （ $m$ 为整数）进行如下变形： $M = \frac{m^{2} - 2 m + 1}{m^{2} - 1} = \frac{m - 1}{m + 1} = \frac{(m + 1) - 2}{m + 1} = 1 - \frac{2}{m + 1}$ ，其中 $m$ 为整数．
结论Ⅰ：依据变形结果可知， $M$ 的值可以为0；
结论Ⅱ：若使 $M$ 的值为整数，则 $m$ 的值有3个．

A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对Ⅱ对 D、Ⅰ对Ⅱ不对

查看试题解析
5. 甲、乙两组同学在植树活动中均植树120棵，已知______，求乙组每小时植树多少棵？
下面是题目的部分解题过程；则横线上缺少的条件为（）
解：设乙组每小时植树x棵．
由题意得： $\frac{120}{x} = \frac{120}{x + 10} + 2$ ，
…

A、甲组每小时比乙组少种植10棵，且甲组比乙组提前2小时完成 B、甲组每小时比乙组多种植10棵，且乙组比甲组提前2小时完成 C、甲组每小时比乙组少种植10棵，且乙组比甲组提前2小时完成 D、甲组每小时比乙组多种植10棵，且甲组比乙组提前2小时完成

查看试题解析
6. 下列各式从左到右的变形，属于因式分解的是（）

A、 $16 x^{2} y^{3} = 2 x y^{2} \cdot 8 x y$ B、 $(x + y) (x - y) = x^{2} - y^{2}$ C、 $x^{2} - x y + y^{2} = {(x - y)}^{2} + x y$ D、 $2 x - 2 y = 2 (x - y)$

查看试题解析
7. 用提公因式法分解因式 $6 x y + 8 x^{2} y - 4 x^{2} y z^{3}$ 时，提取的公因式是（）

A、 $x y$ B、 $2 x z$ C、 $2 x y$ D、 $3 y z$

查看试题解析
8. 某篮球队5名场上队员的身高（单位：cm）分别是：190，194，198，200，202，现用一名身高为 $196 cm$ 的队员换下场上身高为 $190 cm$ 的队员．与换人前相比，下列对5名场上队员身高的平均数和方差描述正确的是（）

A、平均数变小，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变小 D、平均数变大，方差变大

查看试题解析
9. 已知一组数据： $x_{1}, x_{2}, x_{3}, \dots, x_{n}$ 的方差为0.5，则 $2 x_{1} + 1, 2 x_{2} + 1, 2 x_{3} + 1, ⋯, 2 x_{n} + 1$ 这组数据的方差为（）

A、0.5 B、1 C、1.5 D、2

查看试题解析
10. 如图，有 $A$ 型、 $B$ 型、 $C$ 型三种不同的纸板．其中 $A$ 型是边长为 $x$ 的正方形，共有1块； $B$ 型为边长为2的正方形，共有2块； $C$ 型是长为 $x$ ，宽为2的长方形，共有4块．现用这7块纸板去拼出一个大的长方形（不重叠、不留空隙），则下列操作可行的是（）

A、用全部7块纸板 B、加上3块 $B$ 型纸板 C、拿掉2块 $C$ 型纸板 D、加上1块 $A$ 型纸板

查看试题解析

二、填空题：本题共5小题，每小题3分，共15分.

11. 从 $m^{2}$ 、 $2 m n$ 、 $n^{2}$ 这3个单项式中先选择两个或三个组成一个多项式，再进行因式分解，写出一个这样的等式

查看试题解析
12. 若分式 $\frac{x^{2} - 4}{x - 2}$ 的值为零，则 $x$ 的值是．

查看试题解析
13. 若关于 $x$ 的方程 $\frac{2 m + x}{x - 3} - 1 = \frac{2}{x}$ 无解，则 $m$ 的值为．

查看试题解析
14. 在对多项式 $x^{2} + a x + b$ 进行因式分解时，M同学看错了b，分解为 $(x + 2) (x + 4)$ ；N同学看错了a，分解为 $(x - 1) (x - 9)$ ．（两人后面因式分解没有错误），则 $a =$ ， $b =$ ．

查看试题解析
15. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

查看试题解析

三、解答题：本题共8小题，共75分.解答应写出文字说明、证明过程或演算步骤.

16. 因式分解
（1） $- 3 x^{3} y^{2} + 6 x^{2} y^{3} - 3 x y^{4}$ ；（2） $3 x (a - b) - 6 y (b - a)$ ．

查看试题解析
17. 解方程：

(1)、 $\frac{4}{x^{2} - 2 x} + \frac{1}{x} = \frac{2}{x - 2}$ ；

(2)、 $\frac{2}{x - 1} + \frac{x + 2}{1 - x} = 3$

查看试题解析
18. 李老师要从小聪、小亮两人中选拔一人参加知识竞赛，现对两人的5次测试成绩进行整理分析，两人的成绩如下：
小聪：76，80，79，85，80；
小亮：77，79，81，82，81．
李老师将两人的成绩分析如下：（单位：分）．

平均成绩
中位数
众数
小聪
a
80
c
小亮
80
b
81

(1)、填空：a＝；b＝；c＝．

(2)、李老师已经求得小聪5次测试成绩的方差S²＝8.4，请你帮助李老师计算小亮5次测试成绩的方差．

(3)、根据以上信息，请你运用所学的统计知识帮助李老师作出选择，并说明理由．

查看试题解析
19. 一般情况下，一个分式通过适当的变形，我们可以把它化成一个整式和一个分子是整数的分式的和的形式，例如：
① $\frac{x + 1}{x - 1} = \frac{(x - 1) + 2}{x - 1} = 1 + \frac{2}{x - 1}$ ；
② $\frac{x^{2}}{x - 2} = \frac{x^{2} - 4 + 4}{x - 2} = \frac{(x + 2) (x - 2) + 4}{x - 2} = (x + 2) + \frac{4}{x - 2}$ ；
③ $\frac{x^{3}}{x - 1} = \frac{x^{3} - x^{2} + x^{2}}{x - 1} = x^{2} + \frac{x^{2}}{x - 1} = \dots$

(1)、仿照上述方法，试将分式 $\frac{x + 7}{x + 3} ， \frac{2 x^{2} - 1}{x + 1}$ 化为一个整式和一个分子是整数的分式的和的形式；

(2)、仿照上述方法，把 $\frac{x^{3}}{x + 3}$ 化成一个整式和一个分子是整数的分式的和的形式；

(3)、已知x、y均为正整数， $M = \frac{x}{x - 5} ， N = \frac{7 y}{7 y - 5}$ ，且M、N均为正数．若M+N＝3，请求出x、y的值．

查看试题解析
20. 阅读下列材料：
对于多项式x²+x-2，如果我们把x=1代入此多项式，.发现x²+x-2的值为0，这时可以确定多项式中有因式（x-1）；同理，可以确定多项式中有另一个因式（x+2），于是我们可以得到：x²+x-2=（x-1）（x+2）.
又如：对于多项式2x²-3x-2，发现当x=2时，2x²-3x-2的值为0，则多项式2x²-3x-2有一个因式（x-2），我们可以设2x²-3x-2=（x-2）（mx+n），解得m=2， n=1，于是我们可以得到：2x²-3x-2=（x-2）（2x+1）
请你根据以上材料，解答以下问题：

(1)、当x=时，多项式8x²-x-7的值为0，所以多项式8x²-x-7有因式，从而因式分解8x²-x-7=.

(2)、以上这种因式分解的方法叫试根法，常用来分解一些比较复杂的多项式，请你尝试用试根法分解多项式：
①3x²+11x+10
②x²－21x+20

查看试题解析

21. 支付宝、微信、现金、其他移动支付（每人只选一项），形成如下调查报告：

课题主题	“移动支付方便你我他”﹣移动支付在人们生活中的作用
活动目标	了解移动支付的使用情况和发展前景，增强社会责任意识，科技创新意识
调查方式	抽样调查
数据的收集、整理与描述	手机支付是中国移动面向用户提供的一项综合性移动支付服务，可使用支付账户完成生活消费、缴话费、网上购物、水电燃气账单支付等远程消费．
	移动支付的调查问卷您好！这是一份关于移动支付方式的问卷调查，请选择一项您最常使用的方式（只选一项），在其后的括号内打“√”，非常感谢您的配合！	移动支付方式 A ．支付宝支付 ____ B ．微信支付 ____ C ．现金支付 ____ D ．其他移动支 ____

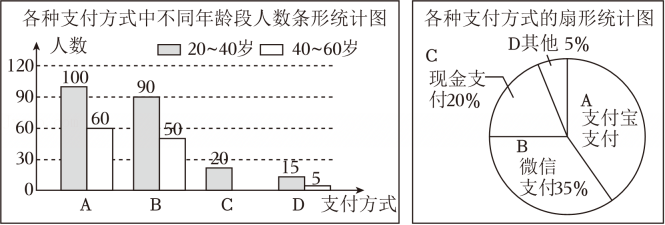
调查结果	…

任务二：解决问题

请根据以上调查报告，解答下列问题：

(1)、这次调查的样本容量是 ▲ ；并补全条形统计图；

(2)、根据条形统计图可得，该社区中20～40岁居民使用支付宝、微信、现金、其他移动支付人数分别为100、90、20、15，这四个数据的中位数是；

(3)、该社区中40～60岁的居民约6000人，估算这些人中最喜欢用“支付宝”支付方式的人数．

查看试题解析

22. 学校为了让学生进行物理实验的体验和实验效果更好，决定向相关部门申请采购一批新的电流表和电压表.已知市场上电流表的单价比电压表的单价高20%，且学校计划购买电流表和电压表共150台，其中购买电流表花费3 840元，购买电压表花费1600 元.

(1)、电压表的单价是多少元?

(2)、因原材料市场价格浮动，实验仪器厂商计划对电流表的售价提高20%，电压表的售价为原来的8折，若学校计划再次购进的电流表和电压表的总费用不超过3 800元，且两种仪器共购买100 台，则学校最多可以购买电流表多少台?

查看试题解析
23. 新定义：如果两个实数 $a$ ， $b$ 使得关于 $x$ 的分式方程 $\frac{a}{x} + 1 = b$ 的解是 $x = \frac{1}{a + b}$ 成立，那么我们就把实数 $a$ ， $b$ 组成的数对 $[a ， b]$ 称为关于 $x$ 的分式方程 $\frac{a}{x} + 1 = b$ 的一个“关联数对”．
例如： $a = 2$ ， $b = - 5$ 使得关于 $x$ 的分式方程 $\frac{2}{x} + 1 = - 5$ 的解是 $x = \frac{1}{2 + (- 5)} = - \frac{1}{3}$ 成立，所以数对 $[2 ， - 5]$ 就是关于 $x$ 的分式方程 $\frac{a}{x} + 1 = b$ 的一个“关联数对”．

(1)、判断下列数对是否为关于 $x$ 的分式方程 $\frac{a}{x} + 1 = b$ 的“关联数对”，若是，请在括号内打“√”．若不是，打“×”．
① $[1 ， 1]$ （ ▲ ）；② $[3 ， - 5]$ （ ▲ ）；③ $[- 2 ， 4]$ （ ▲ ）；

(2)、若数对 $[n^{2} ， 8 - n^{2}]$ 是关于 $x$ 的分式方程 $\frac{a}{x} + 1 = b$ 的“关联数对”，求 $n$ 的值；

(3)、若数对 $[m - k ， k]$ （ $m \neq - 1$ 且 $m \neq 0$ ， $k \neq 1$ ）是关于 $x$ 的分式方程 $\frac{a}{x} + 1 = b$ 的“关联数对”，且关于 $x$ 的方程 $k x - m + 1 = \frac{- 2 m}{m + 1} x$ 有整数解，求整数 $m$ 的值．

查看试题解析

	平均成绩	中位数	众数
小聪	a	80	c
小亮	80	b	81