鲁教版(五四制)数学六年级上学期期中仿真模拟试卷二
试卷更新日期:2025-09-18 类型:期中考试
一、选择题:本题共10小题,每小题3分,共30分。每小题只有一个选项符合题目要求.
-
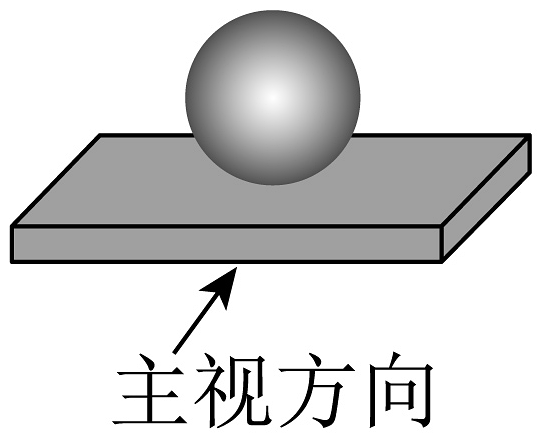
1. 如图是由一个长方体和一个球组成的几何体,它的主视图是( ).
 A、
A、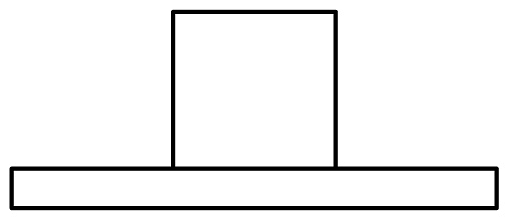 B、
B、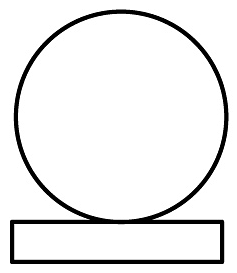 C、
C、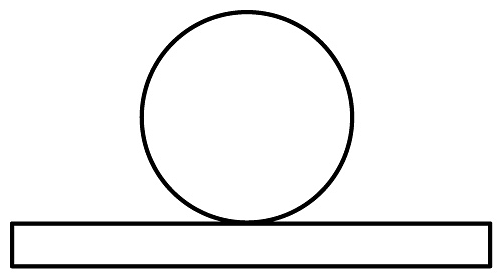 D、
D、 2. “鸣语既过渐细微,映空摇飏如丝飞”是唐代诗人杜甫作品《雨不绝》中的诗句,意为喧哗的雨已经过去,逐渐变得细微,映着天空摇漾如丝的细雨飘飞.诗中描写雨滴下来形成雨丝,用数学语言解释这一现象为( )A、点动成线 B、线动成面 C、面动成体 D、面面相交成线3. 最新数据显示,我国经济运行总体平稳、稳中有进.海关总署发布数据显示,今年前7个月,我国货物进出口总值248300亿元,同比增长了 , 其中248300用科学记数法表示为( )A、 B、 C、 D、4. 一个正方体的表面展开图如图所示,六个面上各有一字,连起来是“祝福祖国万岁”,把它折成正方体后,与“万”相对的字是( ).
2. “鸣语既过渐细微,映空摇飏如丝飞”是唐代诗人杜甫作品《雨不绝》中的诗句,意为喧哗的雨已经过去,逐渐变得细微,映着天空摇漾如丝的细雨飘飞.诗中描写雨滴下来形成雨丝,用数学语言解释这一现象为( )A、点动成线 B、线动成面 C、面动成体 D、面面相交成线3. 最新数据显示,我国经济运行总体平稳、稳中有进.海关总署发布数据显示,今年前7个月,我国货物进出口总值248300亿元,同比增长了 , 其中248300用科学记数法表示为( )A、 B、 C、 D、4. 一个正方体的表面展开图如图所示,六个面上各有一字,连起来是“祝福祖国万岁”,把它折成正方体后,与“万”相对的字是( ).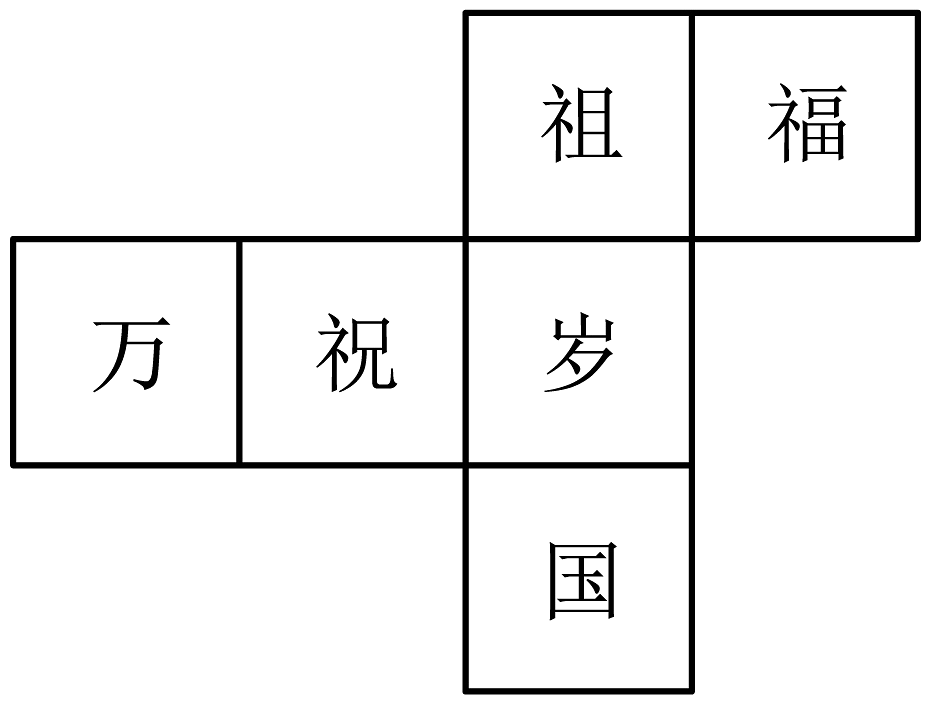 A、祖 B、国 C、岁 D、福5. 若为有理数且 , 则的取值是( )A、5 B、 C、或3 D、6. 下列说法:①符号相反的数互为相反数;②一定是一个负数;③不是正数的数一定是整数;④一个数的绝对值越大,数轴上表示它的点离原点越远;⑤若三个有理数中只有1个负数,则这三个有理数的乘积必为正数;其中正确的有( )A、1个 B、2个 C、3个 D、4个7. 分别用一平面去截如图所示的几何体,能得到截面是长方形的几何体有( )
A、祖 B、国 C、岁 D、福5. 若为有理数且 , 则的取值是( )A、5 B、 C、或3 D、6. 下列说法:①符号相反的数互为相反数;②一定是一个负数;③不是正数的数一定是整数;④一个数的绝对值越大,数轴上表示它的点离原点越远;⑤若三个有理数中只有1个负数,则这三个有理数的乘积必为正数;其中正确的有( )A、1个 B、2个 C、3个 D、4个7. 分别用一平面去截如图所示的几何体,能得到截面是长方形的几何体有( ) A、①②③ B、①②④ C、①③④ D、①③⑤8. 如图,一个正方体的六个面分别标有、、、、、 , 从三个不同方向看到的情况如图所示,则的对面应该是字母( )
A、①②③ B、①②④ C、①③④ D、①③⑤8. 如图,一个正方体的六个面分别标有、、、、、 , 从三个不同方向看到的情况如图所示,则的对面应该是字母( ) A、 B、 C、 D、9. 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为 , , , , 那么可以转换为该生所在班级序号,其序号为.如图2第一行数字从左到右依次为0,1,0,1,序号为 , 表示该生为5班学生.表示6班学生的识别图案是( )
A、 B、 C、 D、9. 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为 , , , , 那么可以转换为该生所在班级序号,其序号为.如图2第一行数字从左到右依次为0,1,0,1,序号为 , 表示该生为5班学生.表示6班学生的识别图案是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 下列说法中,错误的个数是( )
10. 下列说法中,错误的个数是( )①若 , 则;
②若 , 则有是负数:
③A、B、C三点在数轴上对应的数分别是、6、x,若相邻两点的距离相等,则;
④若代数式的值与无关,则该代数式值为2024;
⑤若 , , 则的值为 .
A、1个 B、2个 C、3个 D、4个二、填空题:本题共5小题,每小题3分,共15分.
-
11. 如图,正方体的平面展开图,每个正方形中都标注了一个汉字.反向思考,正方体中,标注“锦”的面的对面标注的汉字是 .
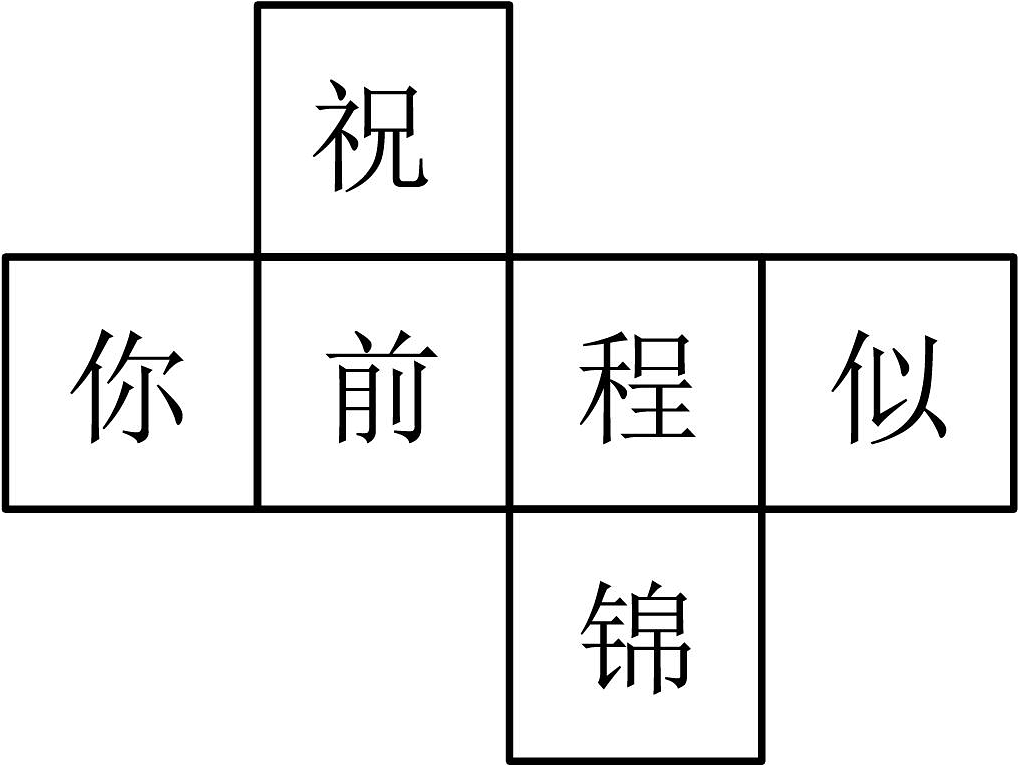 12. 若|a|<|b|<|c|,且a<0,b>0,c<0,比较a,-a,b,-b,c,-c的大小;.(用“<”连接)13. 在图中剪去个小正方形,使得到的图形经过折叠能够围成一个正方体,则要剪去的正方形对应的数字是 .
12. 若|a|<|b|<|c|,且a<0,b>0,c<0,比较a,-a,b,-b,c,-c的大小;.(用“<”连接)13. 在图中剪去个小正方形,使得到的图形经过折叠能够围成一个正方体,则要剪去的正方形对应的数字是 . 14. 按图中的程序运算:当输入的数据为1时,则输出的数据是 .
14. 按图中的程序运算:当输入的数据为1时,则输出的数据是 . 15. 若 , 则
15. 若 , 则三、解答题:本题共8小题,共75分.解答应写出文字说明、证明过程或演算步骤.
-
16. 计算:(1)、(2)、(3)、(4)、17. 把下列序号填在相应的大括号里(只填序号,多填或少填不给分).
①;②;③;④;⑤;⑥;⑦;⑧;⑨0
整数集合{______________________________……}
负有理数集合{______________________________……}
非负数集合{______________________________……}
18. (1)如图,数轴上 , , 各点分别表示什么数?
(2)画出数轴,用数轴上的点表示下列各数: , , , 并用“”将它们连接起来.
19. 对于任意有理数 , 定义一种新运算: .(1)、若 , , 求的值;(2)、已知点 , 点在数轴上表示的数分别为 , , 且 , 两点的距离是 , 是的相反数,求的值.20. 若互为相反数且都不为零,互为倒数, , 求的值.21. 用12个大小相同的小正方体搭成如图所示的几何体,其中,小正方体的棱长为 . (1)、请利用上面的网格画出从正面看和从上面看该几何体的形状图;(2)、图中12个小正方体搭成的几何体的表面积(包括与地面接触的部分)是;(3)、小明用若干个相同的小正方体搭成了另一个几何体,结果发现从正面看和从上面看的形状图与刚才的完全一致,则小明所用的小正方体最多有块.22. 出租车司机老姚某天上午营运全是在南北走向的兴海路上进行,如果规定向南为正,向北为负,他这天上午行车里程(单位:)如下:
(1)、请利用上面的网格画出从正面看和从上面看该几何体的形状图;(2)、图中12个小正方体搭成的几何体的表面积(包括与地面接触的部分)是;(3)、小明用若干个相同的小正方体搭成了另一个几何体,结果发现从正面看和从上面看的形状图与刚才的完全一致,则小明所用的小正方体最多有块.22. 出租车司机老姚某天上午营运全是在南北走向的兴海路上进行,如果规定向南为正,向北为负,他这天上午行车里程(单位:)如下:.
(1)、将第几名乘客送到目的地时,老姚刚好回到上午出发点?(2)、将最后一名乘客送到目的地时,老姚距上午出发点多远?在出发点的南面还是北面?(3)、若汽车耗油量为 , 这天上午老姚的出租车耗油多少L?23. 数轴是分析问题的工具,如图1,小浩在草稿纸上画了一条数轴进行如下探究: (1)、折叠纸面,使数轴上表示3的点与表示的点重合,则表示的点与表示 的点重合;(2)、折叠纸面,若使表示的点与4表示的点重合:
(1)、折叠纸面,使数轴上表示3的点与表示的点重合,则表示的点与表示 的点重合;(2)、折叠纸面,若使表示的点与4表示的点重合:①表示5表示的点与 表示的点重合;
②若数轴上A,B两点之间距离为6(点A在B的左侧),且A,B两点经折叠后重合,则A,B两点表示的数是多少?
(3)、如图2,在数轴上剪下表示和7的两点间的一段纸带,并把纸带两端朝纸带的正中间处折叠,使表示和7的两点重合,则两条折痕处对应的点所表示的数是多少?