浙江省杭州十三中教育集团2017年中考数学三模试卷
试卷更新日期：2017-12-13 类型：中考模拟
一、仔细选一选
-
1. 计算（﹣1）×3的结果是（ ）A、﹣3 B、﹣2 C、2 D、32. 下列图标中是轴对称图形的是（ ）A、
B、
C、
D、
3. 把x2y﹣y分解因式，正确的是（ ）A、y（x2﹣1） B、y（x+1） C、y（x﹣1） D、y（x+1）（x﹣1）4. 为了解某一路口某一时段的汽车流量，小明同学10天中在同一时段统计通过该路口的汽车数量（单位：辆），将统计结果绘制成如下折线统计图：
由此估计一个月（30天）该时段通过该路口的汽车数量超过200辆的天数为（ ）
A、9 B、10 C、12 D、155. 若一个直六棱柱的三视图如图所示，则这个直六棱柱的体积为（ ）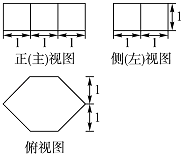
A、4 B、4.5 C、5 D、5.56. 下列关于方程x2+x﹣1=0的说法中正确的是（ ）A、该方程有两个相等的实数根 B、该方程有两个不相等的实数根，且它们互为相反数 C、该方程有一根为 D、该方程有一根恰为黄金比例7. 一个圆锥的侧面展开图是圆心角为120°且半径为6的扇形，则这个圆锥的底面半径为（ ）A、1.5 B、2 C、2.5 D、38. 若二次函数y=x2+bx的图象的对称轴是经过点（2，0）且平行于y轴的直线，则关于x的方程x2+bx=5的解为（ ）A、x1=0，x2=4 B、x1=1，x2=5 C、x1=1，x2=﹣5 D、x1=﹣1，x2=59. 在△ABC中，BC=3 ，AC=5，∠B=45°，对于下面四个结论：①∠C一定是钝角； ②△ABC的外接圆半径为3；③sinA= ；④△ABC外接圆的外切正六边形的边长是 ．其中正确的个数是（ ）
A、1 B、2 C、3 D、410. 已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＞0；②b＜a+c；③4a﹣2b+c＞0；④2c＜3b；⑤当m≤x≤m+1时，函数的最大值为a+b+c，则0≤m≤1；
其中正确的结论有（ ）
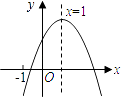A、1个 B、2个 C、3个 D、4个二、认真填一填
-
11. 设n为整数，且n＜ ＜n+1，则n= ．12. 在一个不透明的纸箱内放有除颜色外无其他差别的2个红球，8个黄球和10个白球，从中随机摸出一个球为黄球的概率是 ．
13. 如图，菱形ABCD的面积为120cm2 ， 正方形AECF的面积为50cm2 ， 则菱形的边长为cm．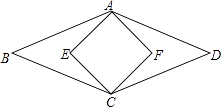
14. 观察下列一组图形中点的个数，其中第1个图形中共有4个点，第2个图形中共有10个点，第3个图形中共有19个点，…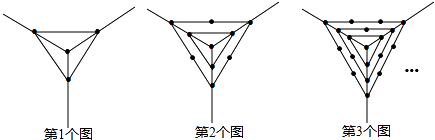
按此规律第5个图形中共有点的个数是 ．
15. 甲、乙两座城市的中心火车站A，B两站相距360km．一列动车与一列特快列车分别从A，B两站同时出发相向而行，动车的平均速度比特快列车快54km/h，当动车到达B站时，特快列车恰好到达距离A站135km处的C站．则动车的平均速度是 ， 特快列车的平均速度是 ．
16. 已知射线OM，ON，∠MON=45°点A在射线OM上，点B在射线ON上，OA=1，若△AOB是轴对称图形，点P为AB的中点，则OP2= ．三、全面答一答
-
17. 计算题
(1)、若a=cos45°，b=（π+1）0 ， c= ，d=（﹣ ）﹣1 ， 化简得a= ， b= ， c= ， d=；
(2)、在（1）的条件下，试计算 ﹣cd．18. 如图，一次函数y1=﹣x+2的图象与反比例函数y2= 的图象相交于A，B两点，与x轴相交于点C．已知tan∠BOC= ，点B的坐标为（m，n）．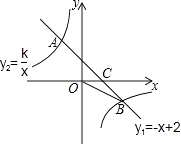
(1)、求反比例函数的解析式；(2)、请直接写出当x＜m时，y2的取值范围．19. 如图，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作AE⊥CD，交CD的延长线于点E，DA平分∠BDE．
(1)、求证：AE是⊙O的切线；
(2)、已知AE=8cm，CD=12cm，求⊙O的半径．
20. 为了解某种电动汽车的性能，对这种电动汽车进行了抽检，将一次充电后行驶的里程数分为 A，B，C，D 四个等级，其中相应等级的里程依次为 200 千米，210 千米，220千米，230 千米，获得如下不完整的统计图．
根据以上信息，解答下列问题：
(1)、问这次被抽检的电动汽车共有几辆？并补全条形统计图；
(2)、估计这种电动汽车一次充电后行驶的平均里程数为多少千米？
21. 如图，已知正方形ABCD，AB=3，点E在线段AB上，AE=1连结DE，DE的垂直平分线交DE于点P，交DC的延长线于点Q，PQ交BC于点G，连结EQ，EQ交BC于点F，连结GE．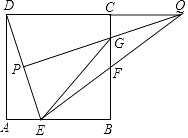
(1)、求证：△ADE∽△PQD；(2)、求线段CQ的长；
(3)、求∠EGB的正切值．
22. 已知二次函数y=4x2﹣4ax+a2﹣2a+2，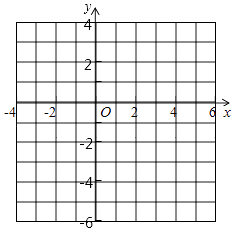
(1)、当a=0，2，4时，请在同一直角坐标系中画出对应函数图象的顶点，并画出a=2 时的函数图象；(2)、证明当a取任意实数时，顶点在一条确定的直线上；(3)、求（2）中的直线被抛物线y=4x2﹣4ax+a2﹣2a+2截得的线段长．23. 定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．如图1中的BD和CE就是两条三分线．
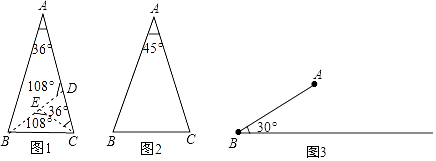(1)、请你在图2中画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数（画出一种即可）；
(2)、△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，请在图3上画出示意图；
(3)、在（2）的前提下，设∠C=x°，试求出x所有可能的值．