内蒙古赤峰市宁城县2017年中考数学二模试卷
试卷更新日期:2017-12-13 类型:中考模拟
一、选择题:
-
1. 下列各数中,最小的数是( )A、5 B、﹣3 C、0 D、22. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
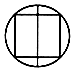 B、
B、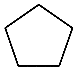 C、
C、 D、
D、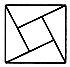 3. 下列运算的结果中,是正数的是( )A、(﹣2007)﹣1 B、(﹣1)2007 C、(﹣1)×(﹣2007) D、(﹣2007)÷20074. 宁城县著名AAAA级景区之一﹣﹣﹣紫蒙湖(原打虎石水库)总面积为400 公顷,总蓄水量为11960 万立方米.数字11960 万立方米用科学记数法表示为( )立方米.A、1.196×109 B、1.196×108 C、1.196×104 D、11.96×1085. 下列运算正确的是( )A、5m+2m=7m2 B、﹣2m2•m3=2m5 C、(﹣a2b)3=﹣a6b3 D、(b+2a)(2a﹣b)=b2﹣4a26. 如图,有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD等于( )
3. 下列运算的结果中,是正数的是( )A、(﹣2007)﹣1 B、(﹣1)2007 C、(﹣1)×(﹣2007) D、(﹣2007)÷20074. 宁城县著名AAAA级景区之一﹣﹣﹣紫蒙湖(原打虎石水库)总面积为400 公顷,总蓄水量为11960 万立方米.数字11960 万立方米用科学记数法表示为( )立方米.A、1.196×109 B、1.196×108 C、1.196×104 D、11.96×1085. 下列运算正确的是( )A、5m+2m=7m2 B、﹣2m2•m3=2m5 C、(﹣a2b)3=﹣a6b3 D、(b+2a)(2a﹣b)=b2﹣4a26. 如图,有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,则CD等于( ) A、 cm B、 cm C、 cm D、 cm7. 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A、 cm B、 cm C、 cm D、 cm7. 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )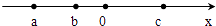 A、ac>bc B、|a﹣b|=a﹣b C、﹣a<﹣b<c D、﹣a﹣c>﹣b﹣c8. 把一块直尺与一块三角板如图放置,若sin∠1= ,则∠2的度数为( )
A、ac>bc B、|a﹣b|=a﹣b C、﹣a<﹣b<c D、﹣a﹣c>﹣b﹣c8. 把一块直尺与一块三角板如图放置,若sin∠1= ,则∠2的度数为( ) A、120° B、135° C、145° D、150°9. 某文具店三月份销售铅笔100支,四、五两个月销售量连续增长.若月平均增长率为x,则该文具店五月份销售铅笔的支数是( )A、100(1+x) B、100(1+x)2 C、100(1+x2) D、100(1+2x)10. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
A、120° B、135° C、145° D、150°9. 某文具店三月份销售铅笔100支,四、五两个月销售量连续增长.若月平均增长率为x,则该文具店五月份销售铅笔的支数是( )A、100(1+x) B、100(1+x)2 C、100(1+x2) D、100(1+2x)10. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )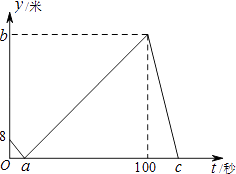 A、①②③ B、仅有①② C、仅有①③ D、仅有②③11. 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
A、①②③ B、仅有①② C、仅有①③ D、仅有②③11. 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )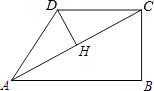 A、
A、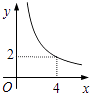 B、
B、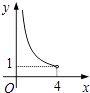 C、
C、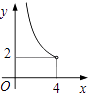 D、
D、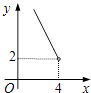
二、填空题
-
12. 计算:( +1)0﹣3tan30°+(﹣1)2017﹣( )﹣1= .13. 底面周长为10πcm,高为12cm的圆锥的侧面积为 .14. 如图,点A在函数y= (x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为 .
 15. 如图,依次以三角形、四边形、…、n边形的各顶点为圆心画半径为1的圆,且圆与圆之间两两不相交.把三角形与各圆重叠部分面积之和记为S3 , 四边形与各圆重叠部分面积之和记为S4 , ….n边形与各圆重叠部分面积之和记为Sn . 则S2017的值为 . (结果保留π)
15. 如图,依次以三角形、四边形、…、n边形的各顶点为圆心画半径为1的圆,且圆与圆之间两两不相交.把三角形与各圆重叠部分面积之和记为S3 , 四边形与各圆重叠部分面积之和记为S4 , ….n边形与各圆重叠部分面积之和记为Sn . 则S2017的值为 . (结果保留π)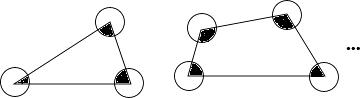
三、解答题
-
16. 解不等式组 写出符合不等式组的整数解,并求出这些整数解中能使关于x的方程:2x+k=﹣1的解为非负数的概率.17. 已知△ABC中,∠A=25°,∠B=40°.
 (1)、求作:⊙O,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求尺规作图,保留作图痕迹,不必写作法)
(1)、求作:⊙O,使得⊙O经过A、C两点,且圆心O落在AB边上.(要求尺规作图,保留作图痕迹,不必写作法)
(2)、求证:BC是(1)中所作⊙O的切线.18. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分分组
家庭用水量x/吨
家庭数/户
A
0≤x≤4.0
4
B
4.0<x≤6.5
13
C
6.5<x≤9.0
D
9.0<x≤11.5
E
11.5<x≤14.0
6
F
x>14.0
3
根据以上信息,解答下列问题
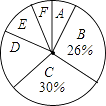 (1)、家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(1)、家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)、本次调查的家庭数为户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)、家庭用水量的中位数落在组;
(4)、若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
19. 如图,直线y=ax+b与反比例函数 (x>0)的图象交于A(2,4),B(4,n)两点,与x轴,y轴分别交于C,D两点.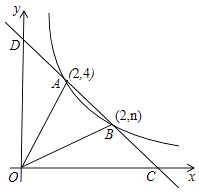 (1)、求m,n的值;
(1)、求m,n的值;
(2)、求△AOB的面积;
(3)、若线段CD上的点P到x轴,y轴的距离相等.求点P的坐标.
20. 已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?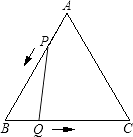 21. 某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
21. 某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)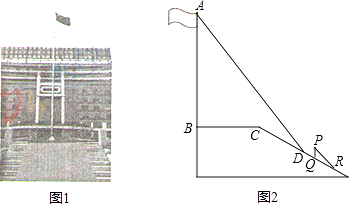 22. “汉十”高速铁路襄阳段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的 ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
22. “汉十”高速铁路襄阳段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的 ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)、若乙队单独施工,需要多少天才能完成该项工程?(2)、若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
23. 已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d= 计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= = = = .
根据以上材料,解答下列问题:
(1)、求点P(1,﹣1)到直线y=x﹣1的距离;
(2)、已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= x+9的位置关系并说明理由;
(3)、已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
24. 如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.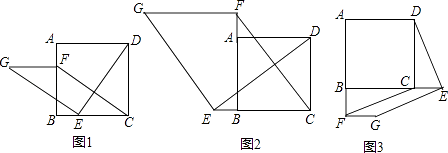 (1)、请判断:FG与CE的数量关系和位置关系;(不要求证明)(2)、如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;
(1)、请判断:FG与CE的数量关系和位置关系;(不要求证明)(2)、如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;
(3)、如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.25. 已知二次函数y=ax2+bx﹣3经过A(﹣1,0),B(3,0)两点,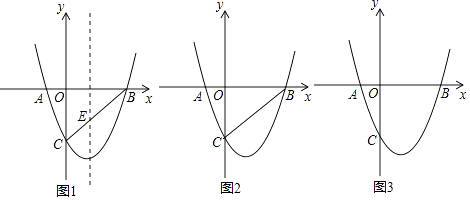 (1)、求二次函数解析式及对称轴方程;
(1)、求二次函数解析式及对称轴方程;
(2)、连接BC,交对称轴于点E,求E点坐标;
(3)、在y轴上是否存在一点M,使△BCM为等腰三角形?若存在,直接写出点M的坐标;若不存在,请说明理由;
(4)、在第四象限内抛物线上是否存一点H,使得四边形ACHB的面积最大?若存在,求出点H坐标;若不存在,说明理由.