河北省承德市双桥区2017年中考数学一模试卷
试卷更新日期:2017-12-13 类型:中考模拟
一、选择题
-
1. 下列各组数中,互为相反数的是( )A、2和﹣2 B、﹣2和 C、﹣2和 D、 和22. 下列等式一定成立的是( )A、2a2﹣3a2=﹣a2 B、(a+2)2=a2+4 C、a6÷a3=a2 D、(a+3)(a﹣3)=a2﹣33. 估计5﹣ 介于( )
A、4与1之间 B、1与2之间 C、2与3之间 D、3与4之间4. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、5. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、 B、
B、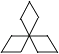 C、
C、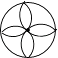 D、
D、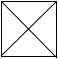 6. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )
6. 如图,直线a∥b,∠1=60°,∠2=40°,则∠3等于( )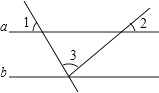 A、40° B、60° C、80° D、100°7. 一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是( )
A、40° B、60° C、80° D、100°7. 一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是( )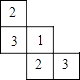 A、
A、 B、
B、 C、
C、 D、
D、 8. 某制药厂两年前生成1吨某种药品的成本是100万元,随着生产技术的进步,现在生产1吨这种药品的成本为81万元,设这种药品成本的年平均下降率为x,根据题意所列方程为( )
8. 某制药厂两年前生成1吨某种药品的成本是100万元,随着生产技术的进步,现在生产1吨这种药品的成本为81万元,设这种药品成本的年平均下降率为x,根据题意所列方程为( )
A、100(1+x)2=81 B、100(1﹣x)2=81 C、81(1+x)2=100 D、81(1﹣x)2=1009. 在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸出一个小球不放回,再随机地摸出一个小球,则两次摸出的小球的标号的和为奇数的概率是( )
A、 B、 C、 D、10. 如图,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分的面积为( ) A、1 B、2 C、1+ D、2﹣11.
A、1 B、2 C、1+ D、2﹣11.如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
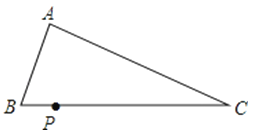 A、
A、 B、
B、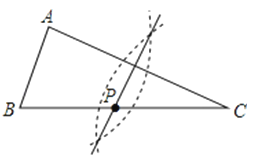 C、
C、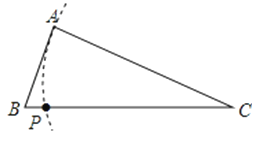 D、
D、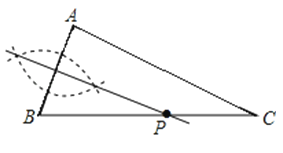 12. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
12. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )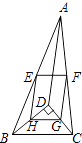 A、7 B、9 C、10 D、1113. 对于非零的两个实数a,b,规定a⊕b=am﹣bn,若3⊕(﹣5)=15,4⊕(﹣7)=28,则(﹣1)⊕2的值为( )A、﹣13 B、13 C、2 D、﹣214. 如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2﹣4ac>0;④a+b+c<0;⑤对于图象上的两点(﹣6,m )、(1,n),有m<n.其中正确信息的个数有( )
A、7 B、9 C、10 D、1113. 对于非零的两个实数a,b,规定a⊕b=am﹣bn,若3⊕(﹣5)=15,4⊕(﹣7)=28,则(﹣1)⊕2的值为( )A、﹣13 B、13 C、2 D、﹣214. 如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2﹣4ac>0;④a+b+c<0;⑤对于图象上的两点(﹣6,m )、(1,n),有m<n.其中正确信息的个数有( ) A、2个 B、3个 C、4个 D、5个15. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:
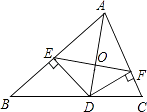
A、2个 B、3个 C、4个 D、5个15. 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列结论:①OA=OD;
②AD⊥EF;
③AE+DF=AF+DE;
④当∠BAC=90°时,四边形AEDF是正方形.
其中一定正确的是( )
 A、①②③ B、②③④ C、①③④ D、①②③④16. 如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
A、①②③ B、②③④ C、①③④ D、①②③④16. 如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( ) A、
A、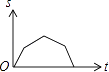 B、
B、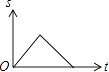 C、
C、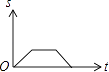 D、
D、
二、填空题
-
17. 计算:2﹣1= .
18. 已知a+b=3,a﹣b=5,则代数式a2﹣b2的值是 .19. 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ,1),则点A8的横坐标是 .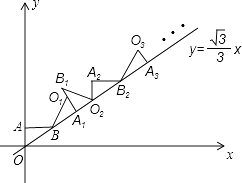
三、解答题
-
20. 计算题
(1)、先化简,再求值: ÷(1+ ),其中x=2017.(2)、已知方程x2﹣2x+m﹣3=0有两个相等的实数根,求m的值.21. 如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ,FC=2 .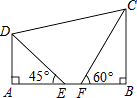 (1)、BC= ;
(1)、BC= ;
(2)、求点D到BC的距离;
(3)、求DC的长.22. 某班要从甲、乙两名同学中选拔出一人,代表班级参加学校的一分钟踢毽子体能素质比赛,在一段时间内的相同条件下,甲、乙两人进行了六场一分钟踢毽子的选拔测试,根据他们的成绩绘制出如图的统计表和不完整的折线统计图.甲、乙两人选拔测试成绩统计表
甲成绩
(次/min)
乙成绩
(次/min)
第1场
87
87
第2场
94
98
第3场
91
87
第4场
85
89
第5场
91
100
第6场
92
85
中位数
91
n
平均数
m
91
并计算出乙同学六场选拔测试成绩的方差:
S乙2= =
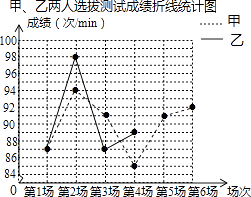 (1)、m= , n= , 并补全全图中甲、乙两人选拔测试成绩折线统计图;
(1)、m= , n= , 并补全全图中甲、乙两人选拔测试成绩折线统计图;
(2)、求甲同学六场选拔测试成绩的方差S甲2;(3)、分别从平均数、中位数和方差的角度分析比较甲、乙二人的成绩各有什么特点?
(4)、经查阅该校以往本项比赛的资料可知,①成绩若达到90次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?②该项成绩的最好记录是95次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
23. 2016年国际马拉松赛于承德市举办,起点承德市狮子园,赛道为外环路,终点为奥体中心(赛道基本为直线).在赛道上有A,B两个服务点,现有甲,乙两个服务人员,分别从A,B两个服务点同时出发,沿直线匀速跑向终点C(奥体中心),如图1所示,设甲、乙两人出发xh后,与B点的距离分别为y甲km、y乙km,y甲、y乙与x的函数关系如图2所示.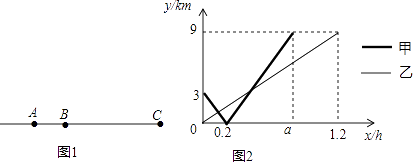 (1)、从服务点A到终点C的距离为km,a=h;(2)、求甲乙相遇时x的值;(3)、甲乙两人之间的距离应不超过1km时,称为最佳服务距离,从甲、乙相遇到甲到达终点以前,保持最佳服务距离的时间有多长?24. 综合题 ——
(1)、从服务点A到终点C的距离为km,a=h;(2)、求甲乙相遇时x的值;(3)、甲乙两人之间的距离应不超过1km时,称为最佳服务距离,从甲、乙相遇到甲到达终点以前,保持最佳服务距离的时间有多长?24. 综合题 ——
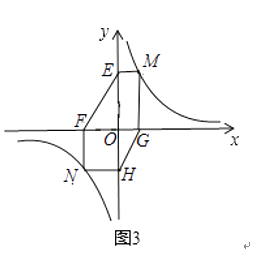
(1)、探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.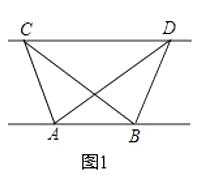 (2)、结论应用:
(2)、结论应用:①如图2,点M、N在反比例函数y= (k>0)的图象上,过点M作ME⊥y轴,垂足分别为E,F,试证明:MN∥EF;
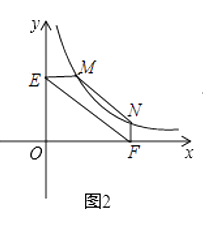
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与EF是否平行.
 25. 为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.张刚按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
25. 为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.张刚按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)、张刚在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)、设张刚获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(3)、物价部门规定,这种节能灯的销售单价不得高于25元.如果张刚想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?26. 矩形ABCD中,BC=3,AB=8,E、F为AB、CD边上的中点,如图1,A在原点处,点B在y轴正半轴上,点C在第一象限,若点A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,则点B随之沿y轴下滑,并带动矩形ABCD在平面上滑动,如图2,设运动时间表示为t秒,当B到达原点时停止运动.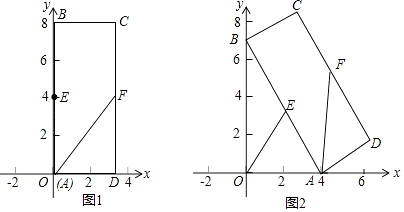 (1)、当t=0时,求点F的坐标及FA的长度;
(1)、当t=0时,求点F的坐标及FA的长度;
(2)、当t=4时,求OE的长及∠BAO的大小;
(3)、求从t=0到t=4这一时段点E运动路线的长;(4)、当以点F为圆心,FA为半径的圆与坐标轴相切时,求t的值.