北师大版数学七年级上学期期中仿真模拟试卷一（范围：1-3章）

试卷更新日期：2025-09-07 类型：期中考试

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分）

1. -6的相反数为（）

A、-6 B、6 C、 $- \frac{1}{6}$ D、 $\frac{1}{6}$

查看试题解析
2. 据报道，2024年国庆假期期间，全国国内出游人数约765000000，将数据765000000用科学记数法表示为（）

A、 $7.65 \times 10^{8}$ B、 $7.65 \times 10^{7}$ C、 $76.5 \times 10^{7}$ D、 $0.765 \times 10^{9}$

查看试题解析
3. 如图，把图形绕着给定的直线旋转一周后形成的几何体是（　　）

A、 B、 C、 D、

查看试题解析
4. 下列说法正确的是（）

A、所有的整数都是正数 B、整数和分数统称有理数
C、 $0$ 是最小的有理数 D、零既可以是正整数，也可以是负整数

查看试题解析
5. 下列判断中，正确的是 ( )

A、 $5 x^{2} y z$ 与yzx²不是同类项 B、 $\frac{2 a^{2} b}{3}$ 的系数是2 C、单项式 $- a^{3} b c$ 的次数是5 D、 $3 m^{2} - n + 5 m n^{5}$ 是二次三项式

查看试题解析
6. 下列每个平面图形均由6个大小相同的小正方形组成，其中不能折叠成正方体的是（）

A、 B、 C、 D、

查看试题解析
7. 以下是嘉淇做填空题的结果： $- 3 x^{2} + (3 x - 4 x^{2}) - ($ $+ 6 + 2 x^{2}) = - 9 x^{2} + 6 x - 6$ ，已知她的计算结果是正确的，但“”处被墨水弄脏看不清了，“”处应是（）

A、 $3 x$ B、 $- 3 x$ C、 $3 x^{2}$ D、 $- 3 x^{2}$

查看试题解析
8. 《庄子》中记载：“一尺之棰，日取其半，万世不竭．”这句话的意思是一尺长的木棍，每天截取它的一半，永远也截不完．若按此方式截一根长为1的木棍，第4天截取后木棍剩余的长度是（）

A、 $1 - \frac{1}{2^{5}}$ B、 $1 - \frac{1}{2^{4}}$ C、 $\frac{1}{2^{5}}$ D、 $\frac{1}{2^{4}}$

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

9. 比较大小： $- \frac{2}{3}$ $- \frac{3}{4}$ ．

查看试题解析
10. 点A，B，C在同一条数轴上，其中点A，B表示的数分别为-3，1，若BC=2，则AC的值为.

查看试题解析
11. 已知 $|x + 3| + {(y - 2)}^{2} = 0 ，$ 则 ${(x + y)}^{2024} =$ ．

查看试题解析
12. 代数式 $\frac{a}{|a|} + \frac{b}{|b|} + \frac{a b}{|a b|}$ 的所有可能的值有．

查看试题解析
13. 有一种“二十四点”的游戏，其游戏规则如下：将四个有理数（每个数都必须用到且只能用一次）进行加减乘除四则运算（可以添加括号），使其结果等于24．现有四个数2， $- 4$ ， 6， $- 9$ ，运用上述规则写出一道算式，使其结果等于24，则算式是 $= 24$ （答案不唯一，只填一个）．

查看试题解析

三、解答题（本大题共7小题，共61分）

14. 计算.

(1)、 $(\frac{1}{2} - \frac{5}{9} + \frac{7}{12}) \times (- 36)$ ；

(2)、 $[2 - 5 \times {(- \frac{1}{2})}^{2}] \div (- \frac{1}{4})$

(3)、 $1 \frac{1}{2} \times \frac{5}{7} - (- \frac{5}{7}) \times 2 \frac{1}{2} + (- \frac{1}{2}) \div 1 \frac{2}{5}$

(4)、 $- 1^{4} - [1 - (1 - 0.5 \times \frac{1}{3}) \times 6]$

查看试题解析
15. 先化简，再求值： $10 y^{2} + 3 (x - 2 y^{2}) - (3 y^{2} + 7 x)$ ，其中 $x = - \frac{1}{4}$ ， $y = 5$ ．

查看试题解析
16. 如图1是由小正方体搭成的几何体

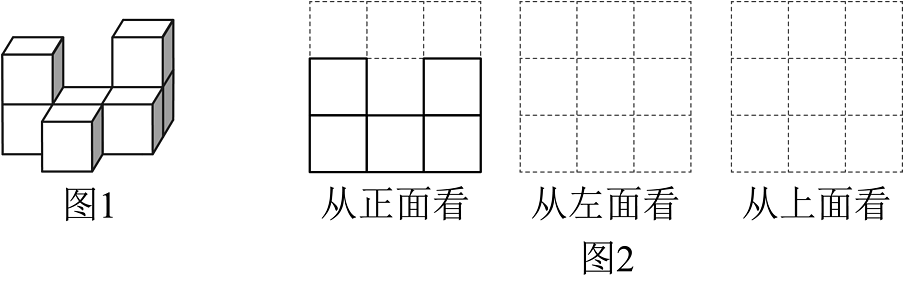(1)、图中已画出从正面看到的形状图，请你利用图2中的网格画出这个几何体从左面看和从上面看到的形状图；

(2)、增加大小相同的小正方体，使得它从上面和左面看到的形状图与图2方格中所画的形状图相同，则搭这样的一个几何体最多增加个小立方块．

查看试题解析
17. 小红准备将新购买的房子的地面铺上地砖，地面结构如图所示，根据图中所给的数据（单位：米），解答下列问题：

(1)、用含m，n的代数式表示地面的总面积；

(2)、已知 $n = 1.5$ 米，且客厅面积是卫生间面积的9倍，如果铺1平方米地面用地砖的平均费用为200元，那么小红家铺地面用地砖的总费用是多少元？

查看试题解析
18. 近几年时间，全球的新能源汽车发展迅，尤其对于我国来说，新能源汽车产销盘都大幅增加，小明家新换了一辆新能源纯电汽车，他连续7天记录了每天行驶的路程（如表）.以 50km 为标准，多于 50km 的记为“+”，不足50km 的记为“_”，刚好 50km 的记为“0”.

第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程（km）
-8
-12
-16
0
+22
+31
+33

(1)、这7天里路程圾多的一天比最少的一天多走km：

(2)、请求出小明家的新能源汽车这七天一共行驶了多少千米?

(3)、已知汽油车每行驶100kmm用汽油6.5升，汽油价8.2元/升，而新能源汽车每行驶 100k耗电为1度，每度电为0.56元，请估计小明家换成新能源汽车后这7天的行驶费用比原来节省多少钱?

查看试题解析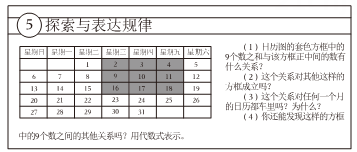
19. 再读教材
请解答教材中的(1)、(2)问。
活学活用
小明是个爱动脑筋的同学，在发现教材中的用方框在月历中移动的规律后，突发奇想，将连续的偶数 $2 ， 4 ， 6 ， 8 ， ⋯$ ，排成如图形式，并用一个十字形框架框住其中的五个数，请你仔细观察十字形框架中的数字的规律，并回答下列问题：

(1)、十字框中的五个数的和与中间的数16有什么关系?

(2)、设中间的数为 $x$ ，用代数式表示十字框中的五个数的和；

(3)、若将十字框上下左右移动，可框住另外的五个数，其它五个数的和能等于2010吗?如能，写出这五个数，如不能，说明理由.

查看试题解析
20. 将一条数轴在原点O和点B处各折一下，得到如图所示的“折线数轴”，图中点A表示 $- 10$ ，点B表示10，点C表示18．我们称点A和点C在数轴上的“友好距离”为28个单位长度．动点P从点A出发，以2单位长度/秒的速度沿着“折线数轴”向其正方向运动．当运动到点O与点B之间时速度变为原来的一半．经过点B后立刻恢复原速；同时，动点Q从点C出发，以1单位长度/秒的速度沿着“折线数轴”向其负方向运动，当运动到点B与点O之间时速度变为原来的两倍，经过O后也立刻恢复原速．设运动的时间为t秒．

(1)、动点P从点A运动至点C需要秒，动点Q从点C运动至点A需要秒；

(2)、P，Q两点相遇时，求出相遇点M在“折线数轴”上所对应的数；

(3)、是否存在t值，使得点P和点Q在“折线数轴”上的“友好距离”等于点A和点B在“折线数轴”上的“友好距离”？若存在，求出t的值；若不存在，请说明理由．

查看试题解析

	第一天	第二天	第三天	第四天	第五天	第六天	第七天
路程（km）	-8	-12	-16	0	+22	+31	+33