第四章《基本平面图形》提升卷—北师大版数学七（上）单元分层测

试卷更新日期：2025-09-07 类型：单元试卷

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分）

1. 下列三个生活中的现象：①用两颗钉子就可以把一根木条固定在墙上；②从A地到B地架设电线，总是尽可能沿着线段 $A B$ 架设；③把弯曲的公路改直，就能缩短路程，其中可用“两点之间，线段最短”来解释的现象有（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
2. 如图，线段AB 上有C，D 两点，CD 的长度为1 cm，AB 的长度为整数，则以A，B，C，D为端点的所有线段的长度之和不可能为( )

A、21 cm B、22 cm C、25 cm D、31 cm

查看试题解析
3. 一条笔直的公路上有A，B，C，D四个村庄，石油公司计划在公路上建设一个加油站，要求加油站到这四个村庄距离之和最小，这样的位置有（）

A、1个 B、2个 C、3个 D、无数个

查看试题解析
4. 在学习完多边形后，小华同学将一个五边形沿如图所示的直线 $l$ 剪掉一个角后，得到一个多边形，下列说法正确的是（）

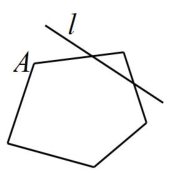A、这个多边形是一个五边形 B、从这个多边形的顶点 $A$ 出发，最多可以画4条对角线 C、从顶点 $A$ 出发的所有对角线将这个多边形分成了4个三角形 D、以上说法都不正确

查看试题解析
5. 如图，甲、乙两人同时从 $A$ 地出发，甲沿北偏东 $48 °$ 方向步行前进，乙沿图示方向步行前进.当甲到达 $B$ 地，乙到达 $C$ 地时，甲与乙前进方向的夹角 $∠ B A C$ 为 $102 °$ ，则此时乙位于 $A$ 地的（）

A、南偏东 $50 °$ B、南偏东 $30 °$ C、北偏西 $30 °$ D、北偏西 $50 °$

查看试题解析
6. 某中学举行越野赛，学生于早上7时在操场集合，裁判长强调了比赛规则和安全方面的注意事项.出发时，裁判长看了手表刚好是7时20分，此刻时针和分针的夹角为 ( )

A、90° B、95° C、100° D、105°

查看试题解析
7. 杨老师到几何王国去散步，刚走到“角”的家门，就听到∠A、∠B、∠C在吵架，∠A说：“我是 $48 ° 1 5^{'}$ ，我应该最大!”∠B说：“我是48.3°，我应该最大!”．∠C也不甘示弱：“我是48.15°，我应该和∠A一样大!”听到这里，杨老师对它们说：“别吵了，你们谁大谁小，由我来作评判!”，杨老师评判的结果是（　　）

A、∠A最大 B、∠B最大 C、∠C最大 D、∠A＝∠C

查看试题解析
8. 在综合与实践课上，将 $∠ A$ 与 $∠ B$ 两个角的关系记为 $∠ A = n ∠ B (n > 0)$ ，探索 $n$ 的大小与两个角的类型之间的关系 $.$ （）

A、当 $n = 2$ 时，若 $∠ A$ 为锐角，则 $∠ B$ 为锐角
B、当 $n = 2$ 时，若 $∠ A$ 为钝角，则 $∠ B$ 为钝角
C、当 $n = \frac{1}{2}$ 时，若 $∠ A$ 为锐角，则 $∠ B$ 为锐角
D、当 $n = \frac{1}{2}$ 时，若 $∠ A$ 为锐角，则 $∠ B$ 为钝角

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

9. 同一条直线上有若干个点，若构成的射线共有10条，则构成的线段共有条.

查看试题解析
10. 某街道分布图如图所示，一个居民要从A处前往B处。如果规定只能按从左到右或从上到下的方向行走，那么该居民可选择的不同路线的条数是。

查看试题解析
11. 如图①，O为直线AB 上一点，作射线OC，使 $∠ A O C ： ∠ B O C =$ 2：1，将一把直角三角尺如图摆放，直角顶点在点O处，一条直角边OP 在射线OA 上.将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转(如图②所示)，在旋转一周的过程中，第t秒时，OQ所在直线恰好平分∠AOC，则t的值为.

查看试题解析
12. 如图所示，已知 $∠ A O B = 128 ° ， O C_{1}$ 平分 $∠ A O B ， O C_{2}$ 平分 $∠ A O C_{1}$ ， $O C_{3}$ 平分 $∠ A O C_{2} ， O C_{4}$ 平分 $∠ A O C_{3}$ ，则 $∠ A O C_{4} =$ ．

查看试题解析
13. 过四边形的一个顶点可以画一条对角线，且把四边形分成两个三角形；过五边形的一个顶点可以画两条对角线，且把五边形分成三个三角形；......猜想：过n边形的一个顶点可以画条对角线，且把n边形分成个三角形.

查看试题解析

三、解答题（本大题共7小题，共61分）

14. 一个扇形的圆心角60°，半径为12cm，求它的面积．（保留π）

查看试题解析
15. 计算(结果用度、分、秒表示)：

(1)、 $33 ° 16^{'} 28^{'}' + 24 ° 46^{'} 37^{'}' .$

(2)、 $132 ° 25^{'} - 55 ° 43^{'} .$

(3)、 $58 ° 45^{'} + 70.3 ° .$

(4)、 $180 ° - (35 ° 47^{'} + 56.5 °) .$

查看试题解析
16. 如图，点A、B、C在同一条直线上，线段 $A B = 4$ ，点C为线段 $A B$ 的中点，在直线 $A B$ 上用尺规作出点D ，使得 $B D = 2 A B$ ，并求 $C D$ 的长度．

(1)、请将小乐的解答过程补充完整；

(2)、请在备用图中用尺规作出其它满足条件的点D ，并求出 $C D$ 的长度．

查看试题解析
17. 用尺规完成下列作图 $($ 保留作图痕迹，不必写作法 $)$

(1)、如图 $1$ ，作图：已知线段 $a ， b (a > b)$ ，作一条线段，使它等于 $a + b$

(2)、如图 $2$ ，已知 $∠ α ， ∠ β$ ，且 $∠ α > ∠ β$ ，作 $∠ D E F$ ，使 $∠ D E F = ∠ α - ∠ β$ ；

(3)、如图 $3$ ，以点 $B$ 为顶点、射线 $B C$ 为一边，作 $∠ E B C$ ，使 $∠ E B C = ∠ A$ ．

查看试题解析
18. 已知直线 $A B$ 经过点O， $∠ C O D = 90 °$ ， $O E$ 是 $∠ B O C$ 的平分线．

(1)、如图1，若 $∠ A O C = 30 °$ ，求 $∠ D O E$ ；

(2)、如图1，若 $∠ A O C = α$ ，求 $∠ D O E$ ；（用含 $α$ 的式子表示）

(3)、将图1中的 $∠ C O D$ 绕顶点O顺时针旋转到图2的位置，其它条件不变，（2）中的结论___________（填“成立”或“不成立”）；

(4)、将图1中的 $∠ C O D$ 绕顶点O逆时针旋转到图3的位置，其它条件不变，求（2）中的结论是否还成立？试说明理由．

查看试题解析
19. 阅读下表：
线段 AB上的点数 n（包括A，B两点）
图形
线段总条数 N
3
∴ C B
3=2+1
4
A^- C D B
6=3+2+1
5
A^- C D E B
10=4+3+2+1
6

7

解答下列问题：

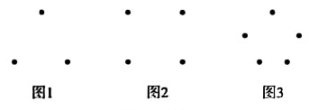
(1)、在表中空白处分别画出图形，写出线段总条数.

(2)、请猜测，线段总条数 N 与线段上的点数n（包括线段的两个端点）有什么关系? 请写出来.

(3)、①如果过每两点可以画一条直线，那么请在如图所示的三组图中分别画直线，并回答问题：
图1中最多可以画条直线；
图2中最多可以画条直线；
图3中最多可以画条直线.
归纳结论：如果平面上有 n（n≥3）个点，且每3个点均不在一条直线上，那么最多可以画出条直线（用含 n的代数式表示）.
②某班50名同学在毕业后的一次聚会中，若每两人握一次手问好，则共握次手；最后，每两个人要互赠礼物留念，则共需件礼物.

查看试题解析
20. 新定义：如果∠MON的内部有一条射线OP将∠MON分成的两个角，其中一个角是另一个角的n倍，那么我们称射线OP为∠MON的n倍分线，例如，如图1，∠MOP=4∠NOP，则OP为∠MON的4倍分线。∠NOQ=4∠MOQ，则OQ也是∠MON的4倍分线。

(1)、应用：若∠AOB=60°，OP为∠AOB的二倍分线，且∠BOP>∠POA，则∠BOP=°。

(2)、如图2，点A，O，B在同一条直线上，OC为直线AB上方的一条射线。
①若OP，OQ分别为∠AOC和∠BOC的3倍分线(∠COP>∠POA，∠COQ>∠QOB)。已知∠AOC=120°，则∠POQ= °。
②在①的条件下，若∠AOC=α，∠POQ的度数是否发生变化?若不发生变化，请写出计算过程；若发生变化，请说明理由。
③如图3，已知∠MON=90°，且OM，ON所在射线恰好分别为∠AOC和∠BOC的3倍分线(∠MOC>∠AOM，∠BON>∠CON)，请直接写出∠AOC的度数。

查看试题解析

线段 AB上的点数 n（包括A，B两点）	图形	线段总条数 N
3	∴ C B	3=2+1
4	A^- C D B	6=3+2+1
5	A^- C D E B	10=4+3+2+1
6
7