浙教版数学八年级上学期期中仿真模拟试卷(范围:1-4章)
试卷更新日期:2025-09-07 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 窗花是我国民间传统剪纸艺术.新春到来之际,小雪设计了如下一组窗花,其中为轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若a>b成立,则下列不等式成立的是( )A、a+3<b+3 B、-3a<-3b C、a-3<b-3 D、3. 能说明命题“若 , 则”是假命题的反例可以是( )A、 , B、 , C、 , D、 ,4. 若等腰三角形的两边长分别为 , , 则这个等腰三角形的周长为( )A、 B、 C、或 D、或5. 已知点在第四象限,且 , 则点的坐标是( )A、 B、 C、 D、6. 如图,在中,分别以点 , 为圆心,大于的长为半径作弧,两弧分别交于点 , , 直线分别交与于点和 , 连结 , 若 , 的周长为 , 则的周长是( )
2. 若a>b成立,则下列不等式成立的是( )A、a+3<b+3 B、-3a<-3b C、a-3<b-3 D、3. 能说明命题“若 , 则”是假命题的反例可以是( )A、 , B、 , C、 , D、 ,4. 若等腰三角形的两边长分别为 , , 则这个等腰三角形的周长为( )A、 B、 C、或 D、或5. 已知点在第四象限,且 , 则点的坐标是( )A、 B、 C、 D、6. 如图,在中,分别以点 , 为圆心,大于的长为半径作弧,两弧分别交于点 , , 直线分别交与于点和 , 连结 , 若 , 的周长为 , 则的周长是( )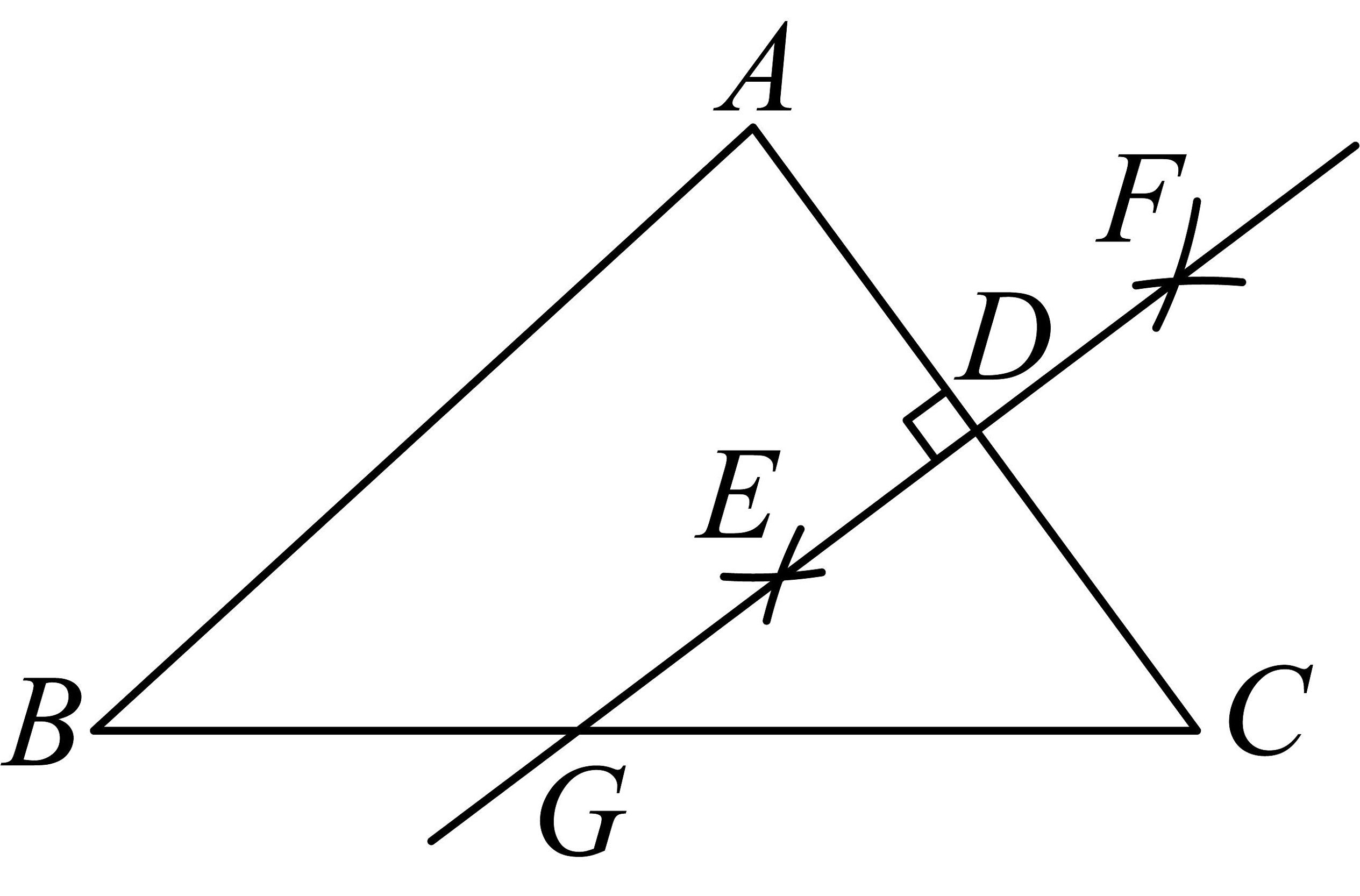 A、 B、 C、 D、7. 如图,平分且于点E, , , 的周长为32,则的面积为( )
A、 B、 C、 D、7. 如图,平分且于点E, , , 的周长为32,则的面积为( ) A、96 B、48 C、32 D、168. 如图,已知的面积为12,点 , 分别为 , 边上的中点,则的面积为( )
A、96 B、48 C、32 D、168. 如图,已知的面积为12,点 , 分别为 , 边上的中点,则的面积为( ) A、3 B、4 C、5 D、69. 如图,在平面直角坐标系中,点的坐标为 , 以线段为边在第四象限内作等边 , 点为轴正半轴上一动点(),设点的坐标为 , 连结 , 以线段为边的第四象限内作等边 , 直线交轴于点 , 点的坐标是( )
A、3 B、4 C、5 D、69. 如图,在平面直角坐标系中,点的坐标为 , 以线段为边在第四象限内作等边 , 点为轴正半轴上一动点(),设点的坐标为 , 连结 , 以线段为边的第四象限内作等边 , 直线交轴于点 , 点的坐标是( ) A、 B、 C、 D、10. 如果关于的不等式组有且只有个整数解,且关于的方程的解为非负整数,则符合条件的所有整数的和为( )A、2 B、3 C、4 D、5
A、 B、 C、 D、10. 如果关于的不等式组有且只有个整数解,且关于的方程的解为非负整数,则符合条件的所有整数的和为( )A、2 B、3 C、4 D、5二、填空题(每小题3分,共18分)
-
11. 如图,在中,是边上的高线,是边上的中线,于F, , 若 , 则 .
 12. 若点关于y轴的对称点是点 , 则 .13. 在数学上用表示不大于的最大整数,例如: , , . 若 , 则的取值范围为 .14. 在△ABC中,AB=AC,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,且DE=4,则AD+AE的值为 .15. 如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .
12. 若点关于y轴的对称点是点 , 则 .13. 在数学上用表示不大于的最大整数,例如: , , . 若 , 则的取值范围为 .14. 在△ABC中,AB=AC,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,且DE=4,则AD+AE的值为 .15. 如图所示,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP= .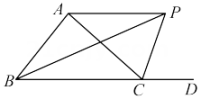 16. 你留意过吗?如图1,硬币上出现的这个多边形是正九边形.现请你仔细分析正九边形的相关特征,完成下面的问题:
16. 你留意过吗?如图1,硬币上出现的这个多边形是正九边形.现请你仔细分析正九边形的相关特征,完成下面的问题:如图2.正九边形中,边 , 的延长线交于点B.

(1)则度;
(2)若 , , , 则a,b,c满足怎样的数量关系?答: .
三、解答题(共8小题,共72分)
-
17. 解下列不等式(组):(1)、;(2)、18. 如图,正方形网格中每个小正方形的边长都为1,的顶点落在格点上,以B为原点建立平面直角坐标系,将关于y轴对称得到 .
 (1)、在网格中建立以B为原点的平面直角坐标系,并画出;(2)、点C关于轴的对称点的坐标为_______;(3)、若点在轴上,且 , 求点的坐标.19. 如图,AB与CB是两条公路,C,D是两个村庄,现在要建一个菜市场,使它到两个村庄的距离相等,而且还要使它到两条公路的距离也相等,用尺规作图画出菜市场的位置.(不写作法,保留作图痕迹)
(1)、在网格中建立以B为原点的平面直角坐标系,并画出;(2)、点C关于轴的对称点的坐标为_______;(3)、若点在轴上,且 , 求点的坐标.19. 如图,AB与CB是两条公路,C,D是两个村庄,现在要建一个菜市场,使它到两个村庄的距离相等,而且还要使它到两条公路的距离也相等,用尺规作图画出菜市场的位置.(不写作法,保留作图痕迹) 20. 如图,点在同一直线上,点在直线的同侧,
20. 如图,点在同一直线上,点在直线的同侧,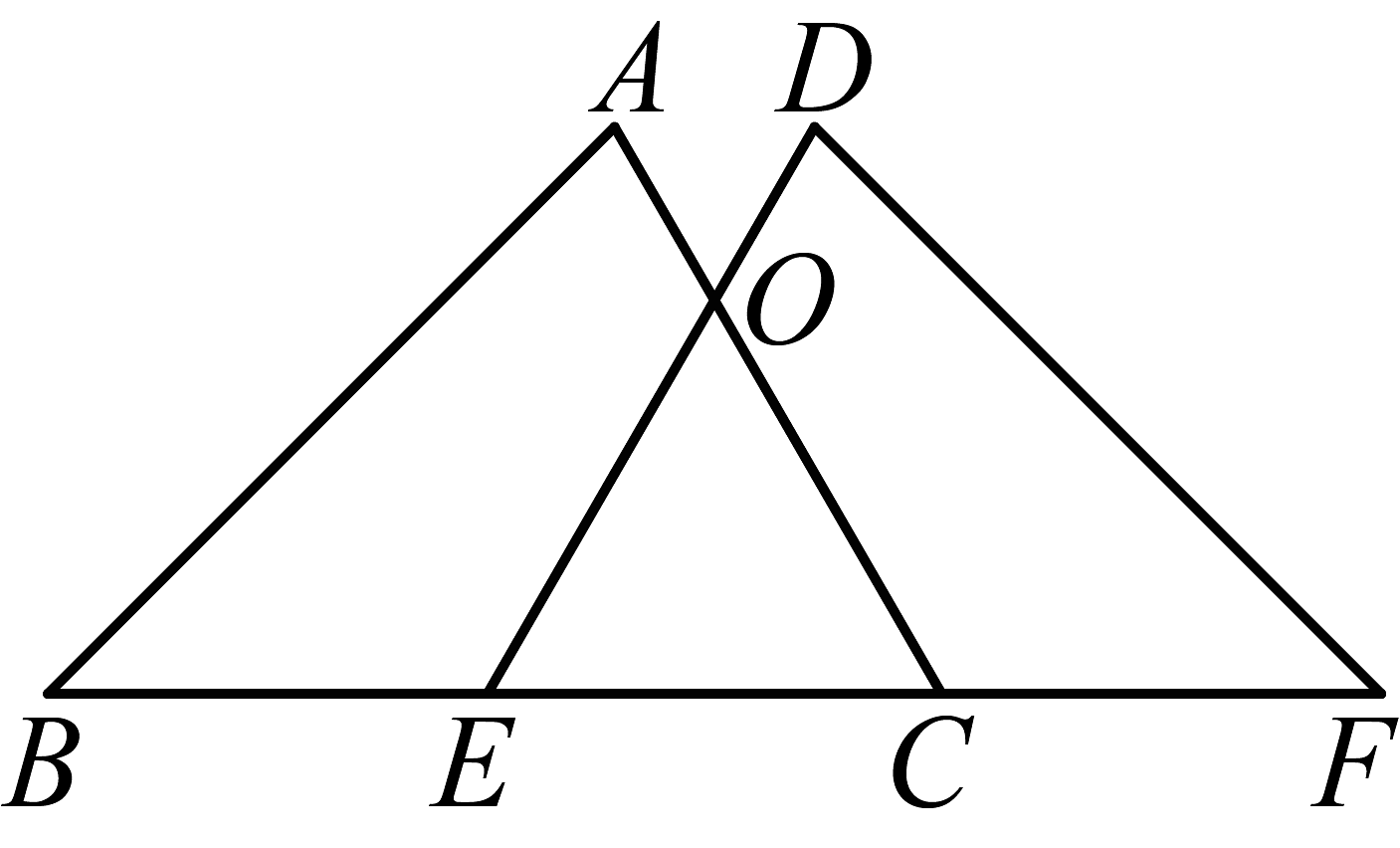 (1)、证明: .(2)、若 , 求的度数.21. 关于x的方程的方程的解满足 .(1)、求a的取值范围;(2)、在(1)的条件下,若不等式的解为 . 求整数a的值.22. 为支援抗击新冠肺炎疫情前线,某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为4万元/吨,乙物资单价为3万元/吨,采购两种物资共花费1920万元.(1)、求甲、乙两种物资各采购了多少吨?(2)、现在计划安排A,B两种不同型号的卡车共50辆来运输这批物资.甲物资7吨和乙物资3吨可装满一辆A型卡车;甲物资5吨和乙物资7吨可装满一辆B型卡车。按此要求安排A、B两型卡车的数量,请问有哪几种运输方案?23. 如图,在等腰直角三角形中, , , 点在边上,作于点 , 连接、 .
(1)、证明: .(2)、若 , 求的度数.21. 关于x的方程的方程的解满足 .(1)、求a的取值范围;(2)、在(1)的条件下,若不等式的解为 . 求整数a的值.22. 为支援抗击新冠肺炎疫情前线,某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为4万元/吨,乙物资单价为3万元/吨,采购两种物资共花费1920万元.(1)、求甲、乙两种物资各采购了多少吨?(2)、现在计划安排A,B两种不同型号的卡车共50辆来运输这批物资.甲物资7吨和乙物资3吨可装满一辆A型卡车;甲物资5吨和乙物资7吨可装满一辆B型卡车。按此要求安排A、B两型卡车的数量,请问有哪几种运输方案?23. 如图,在等腰直角三角形中, , , 点在边上,作于点 , 连接、 .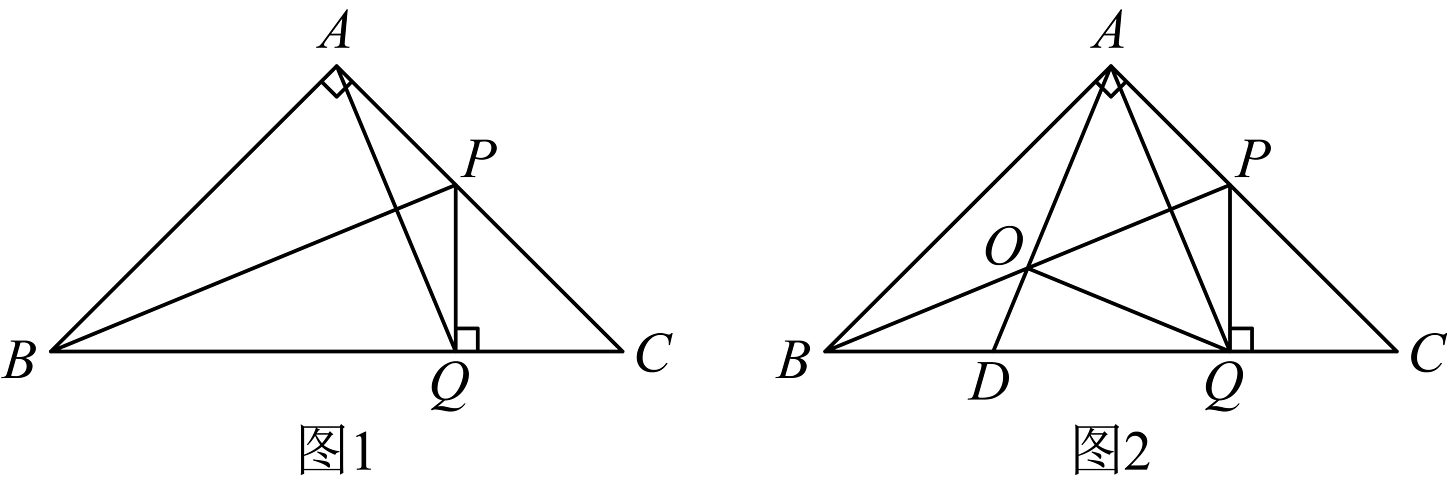 (1)、如图1,若平分 , 求证:垂直平分 .(2)、如图2,点是的中点,直线交于点 , 连接 ,
(1)、如图1,若平分 , 求证:垂直平分 .(2)、如图2,点是的中点,直线交于点 , 连接 ,①求证:是等腰直角三角形.
②若 , , 求的长度.
24. 综合与实践:动手操作:某校八(1)班数学课外兴趣小组在学完第13章的特殊三角形后,利用手头上的一副三角板( , )的直角顶点O放置在另一块直角三角板( , )斜边AB的中点处
发现结论:
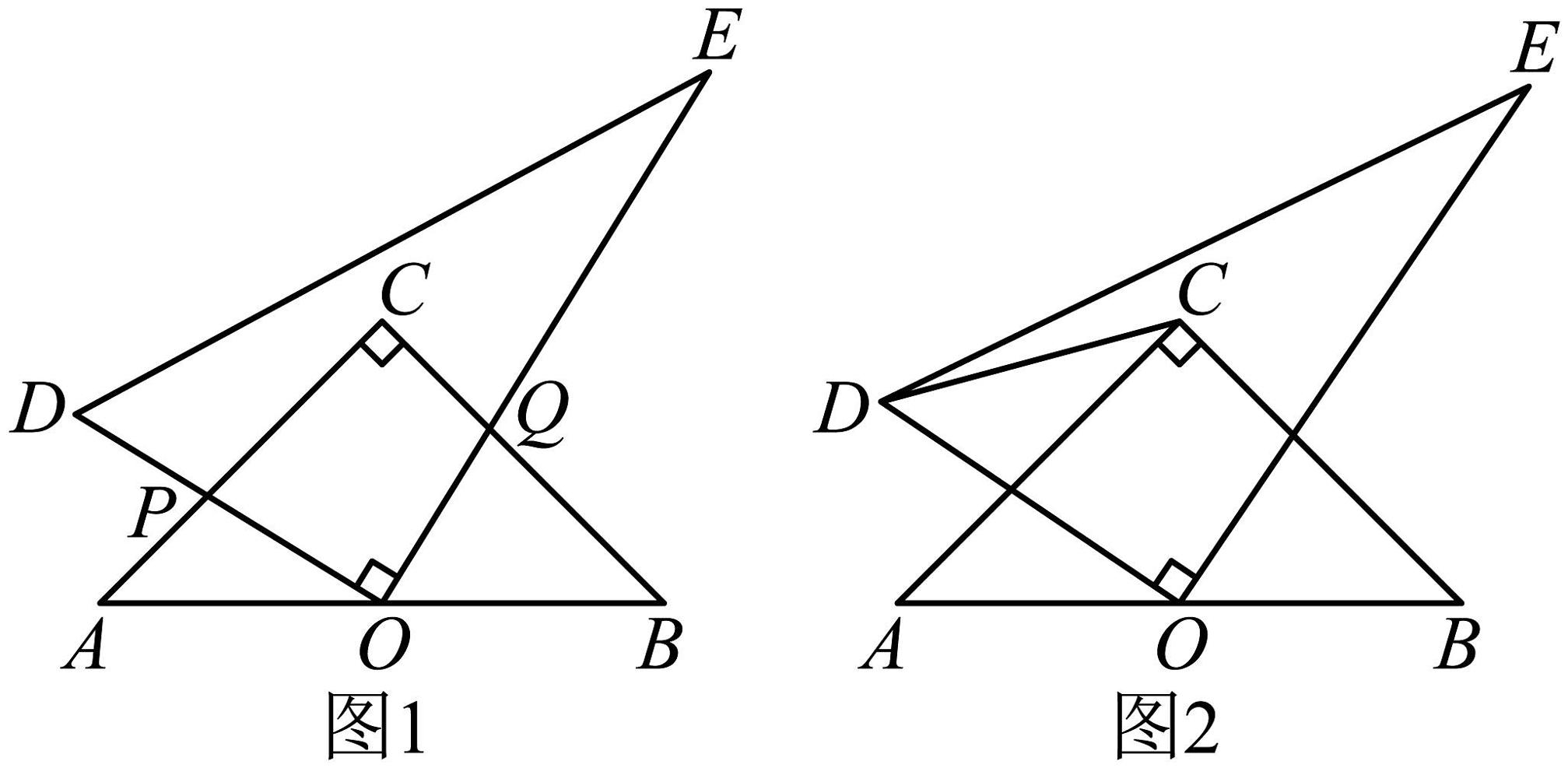
(1)如图1,三角板的两边 , 分别与另一块三角板的边 , 交于点P,Q(规定:此时点P,Q均在边 , 上运动),他们在旋转过程中,发现线段与的长总相等及四边形的面积不会发生变化.
问题解决:
①请你帮他们说明的理由;
②若 , 请你帮他们求出四边形的面积.
拓展延伸:
(2)如图2,连接 , 当 , , 那么直角三角板在绕点O旋转一周的过程中,请你直接写出线段长的最小值和最大值.