浙教版数学八年级上学期期中仿真模拟试卷(范围:1-3章)
试卷更新日期:2025-09-07 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 2024年巴黎奥运会中国体育代表团取得了40金27银24铜的优异成绩,下列巴黎运动会体育图标是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )A、5 B、6 C、11 D、163. 下列式子:①﹣2≤0;②3x+2y>0;③b=2;④m≠3;⑤x+y;⑥x+5≤6;是不等式的有( )A、3个 B、4个 C、5个 D、6个4. 不等式 在数轴上表示正确的是( )A、
2. 已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )A、5 B、6 C、11 D、163. 下列式子:①﹣2≤0;②3x+2y>0;③b=2;④m≠3;⑤x+y;⑥x+5≤6;是不等式的有( )A、3个 B、4个 C、5个 D、6个4. 不等式 在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 为说明命题“若 , 则”是假命题,所列举反例正确的是( )A、 B、 C、 D、6. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就画出一个与原三角形形状大小完全一样(即全等)的三角形,这两个三角形全等的依据为( )
5. 为说明命题“若 , 则”是假命题,所列举反例正确的是( )A、 B、 C、 D、6. 如图,直角三角形被挡住了一部分,小明根据所学知识很快就画出一个与原三角形形状大小完全一样(即全等)的三角形,这两个三角形全等的依据为( ) A、 B、 C、 D、7. 如图,等边中, , 分别是 , , 连结 , 则的度数是( )
A、 B、 C、 D、7. 如图,等边中, , 分别是 , , 连结 , 则的度数是( ) A、 B、 C、 D、无法确定8. 将已知关于x的不等式的解集为 , 则a的取值范围是( )A、 B、 C、 D、9. 如图,中, , 分别以为边在AB的同侧作正三角形 , 图中四块阴影部分的面积分别为 , , , , 则( )
A、 B、 C、 D、无法确定8. 将已知关于x的不等式的解集为 , 则a的取值范围是( )A、 B、 C、 D、9. 如图,中, , 分别以为边在AB的同侧作正三角形 , 图中四块阴影部分的面积分别为 , , , , 则( )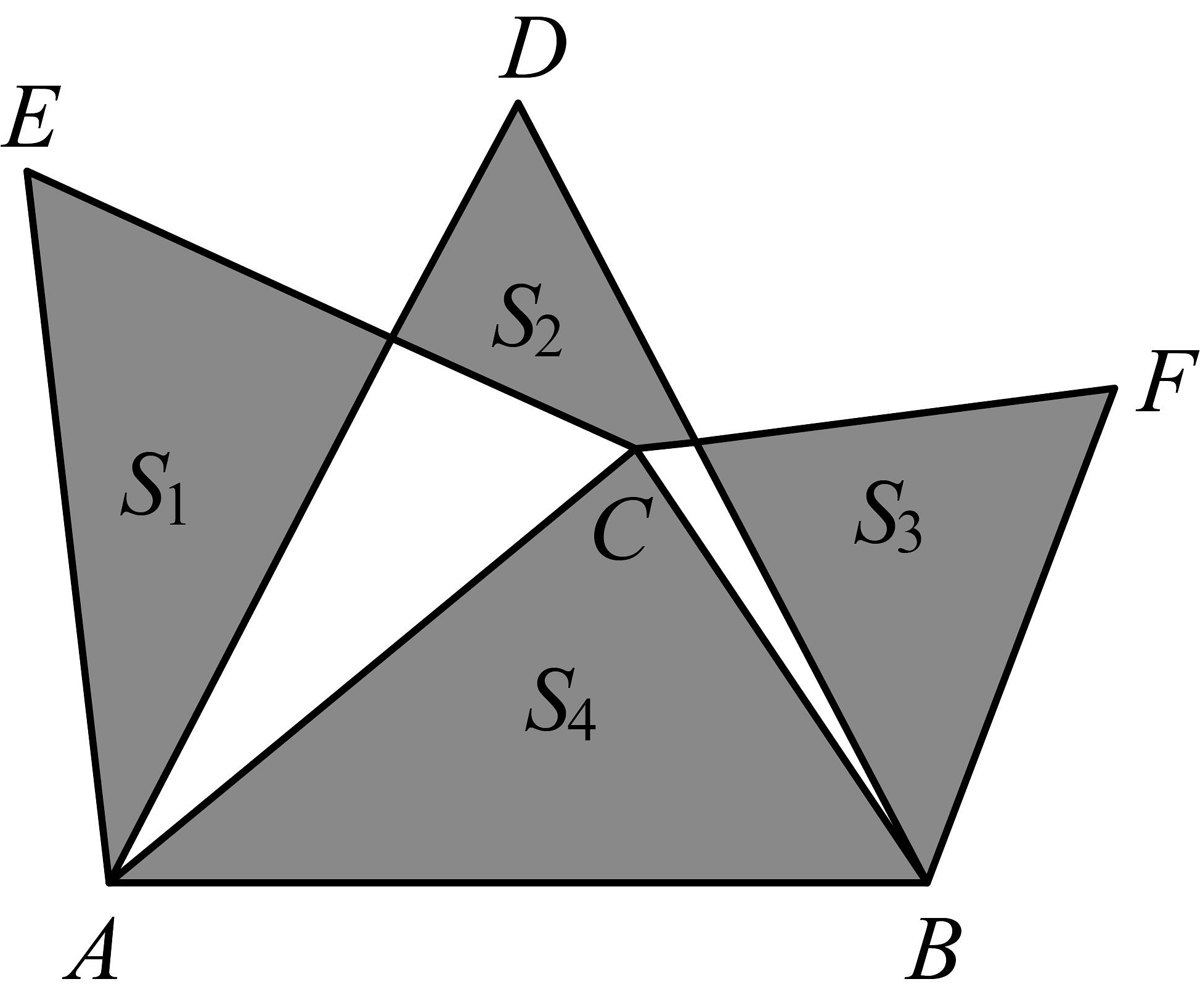 A、 B、 C、 D、10. 如图,在中,和的平分线相交于点O,过O点作交于点E,交于点F,过点O作于D,下列四个结论.(1);(2);③点O到各边的距离相等;④设 , , 则 , 正确的结论有( )
A、 B、 C、 D、10. 如图,在中,和的平分线相交于点O,过O点作交于点E,交于点F,过点O作于D,下列四个结论.(1);(2);③点O到各边的距离相等;④设 , , 则 , 正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每小题3分,共18分)
-
11. 用不等式表示“与的差大于2” .12. 命题“等腰三角形底边上的高线与中线互相重合”的逆命题是13. 两个直角三角形积木 和 按如图所示摆放在水平桌面上, 已知 , , 把下端挂有铅锤的细绳的上端拴在直角顶点 处, 则
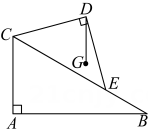 14. 如图是的角平分线,于点 , 若 , , 则的度数是 .
14. 如图是的角平分线,于点 , 若 , , 则的度数是 .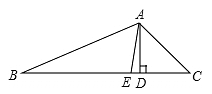 15. 如图,BD是△ABC的中线,CE是ABCD的中线,DF是△CDE的中线,若△ABC的面积为4.则△DEF 的面积为
15. 如图,BD是△ABC的中线,CE是ABCD的中线,DF是△CDE的中线,若△ABC的面积为4.则△DEF 的面积为 16. 如图所示,在等腰中, , 点为射线上的动点, , 且 , 与所在的直线交于点 , 若 , 则 .
16. 如图所示,在等腰中, , 点为射线上的动点, , 且 , 与所在的直线交于点 , 若 , 则 .
三、解答题(共8小题,共72分)
-
17. 解下列不等式(组),并在数轴上表示出来:(1)、;(2)、 .18. 如图,在正方形网格中点A,B, C均为格点,接要求作图(保留作图痕迹,不写作法):
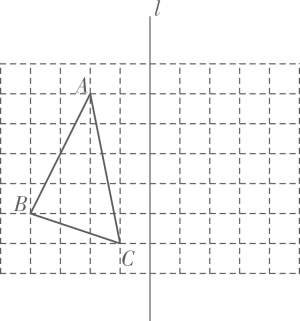 (1)、作出∆ABC关于直线1的对称图形∆A'BC':(2)、求∆ABC的面积;(3)、在直线1上找一点D, 使AD+CD最小.19. 如图,在△ABC中,AB边的垂直平分线l1交BC于点D , AC边的垂直平分线l2交BC于点E , l1与l2相交于点O . 已知△ADE的周长为8cm.
(1)、作出∆ABC关于直线1的对称图形∆A'BC':(2)、求∆ABC的面积;(3)、在直线1上找一点D, 使AD+CD最小.19. 如图,在△ABC中,AB边的垂直平分线l1交BC于点D , AC边的垂直平分线l2交BC于点E , l1与l2相交于点O . 已知△ADE的周长为8cm. (1)、求BC的长;(2)、分别连接OA , OB , OC , 若△OBC的周长为20cm,求OA的长.20. 勾股定理的证明方法多种多样,我国古代数学家赵爽构造“弦图”证明了勾股定理,后人称其为“赵爽弦图”.“赵爽弦图”是由四个全等的直角三角形拼成.如图1为赵爽弦图,其中∠AGB=∠DFA=∠CED=∠BHC=90°,连结AE交BG于点P,连结BE,得到图2,若∠ABE=∠AEB.
(1)、求BC的长;(2)、分别连接OA , OB , OC , 若△OBC的周长为20cm,求OA的长.20. 勾股定理的证明方法多种多样,我国古代数学家赵爽构造“弦图”证明了勾股定理,后人称其为“赵爽弦图”.“赵爽弦图”是由四个全等的直角三角形拼成.如图1为赵爽弦图,其中∠AGB=∠DFA=∠CED=∠BHC=90°,连结AE交BG于点P,连结BE,得到图2,若∠ABE=∠AEB. (1)、求证:EF=DF;(2)、若EF=2,求PE的长.21. 如图,在等边三角形中,点D,E分别在边 , 上,且 , 过点E作 , 交的延长线于点F.
(1)、求证:EF=DF;(2)、若EF=2,求PE的长.21. 如图,在等边三角形中,点D,E分别在边 , 上,且 , 过点E作 , 交的延长线于点F. (1)、求的度数;(2)、求证:是等腰三角形;(3)、若 , 求的长.22. 如图,在△ABC中,、分别是边、上的高线,取的中点为点F , 连结DE , DF , 取的中点为点G .
(1)、求的度数;(2)、求证:是等腰三角形;(3)、若 , 求的长.22. 如图,在△ABC中,、分别是边、上的高线,取的中点为点F , 连结DE , DF , 取的中点为点G . (1)、求证:;(2)、当∠A=60°时,求证:△DEF是等边三角形;(3)、在(2)的条件下,当BC =4时,求FG的长.23. 表格是小聪同学开展项目化学习时填写了部分内容的记录表,
(1)、求证:;(2)、当∠A=60°时,求证:△DEF是等边三角形;(3)、在(2)的条件下,当BC =4时,求FG的长.23. 表格是小聪同学开展项目化学习时填写了部分内容的记录表,项目:测量小山坡的宽度
活动:小山坡的宽度不能直接测量,可以借助一些工具进行测量,比如:皮尺、直角三角板、测角仪、标杆等.各组确定方案后,选择测量工具,画出测量示意图,再进行实地测量,得到具体数据,从而计算出小山坡的宽度.
成果:下面是小聪同学所在小组进行交流展示的部分项目研究内容:
项目
示意图
测量方案
测得数据
测量小山坡的宽度
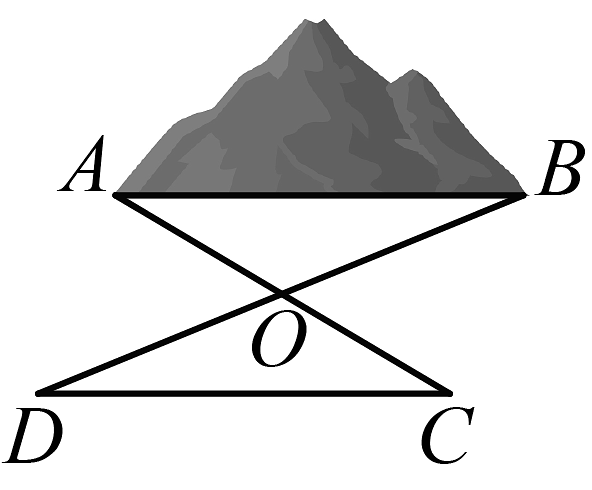
在小山坡外面的平地上找一点 , 立一根标杆,然后再找到点 , 使
, ,
请你帮助小聪同学所在小组完成下列任务.
(1)、任务1:王老师发现小聪同学所在小组的测量方案有问题,请你帮助小聪同学所在小组找到问题并完善测量方案.(2)、任务2:完善方案后请你借助上述测量数据,计算小山坡的宽度 , 并说明理由.(3)、任务3:利用所学知识,请你再设计一个测量方案,并简要说明你的设计思路.24. 某兴趣小组在学习了勾股定理之后提出:“锐(钝)角三角形有没有类似于勾股定理的结论”的问题.首先定义了一个新的概念:如图(1)中,是的中点,是射线上的点,设 . 若 , 则称为勾股比.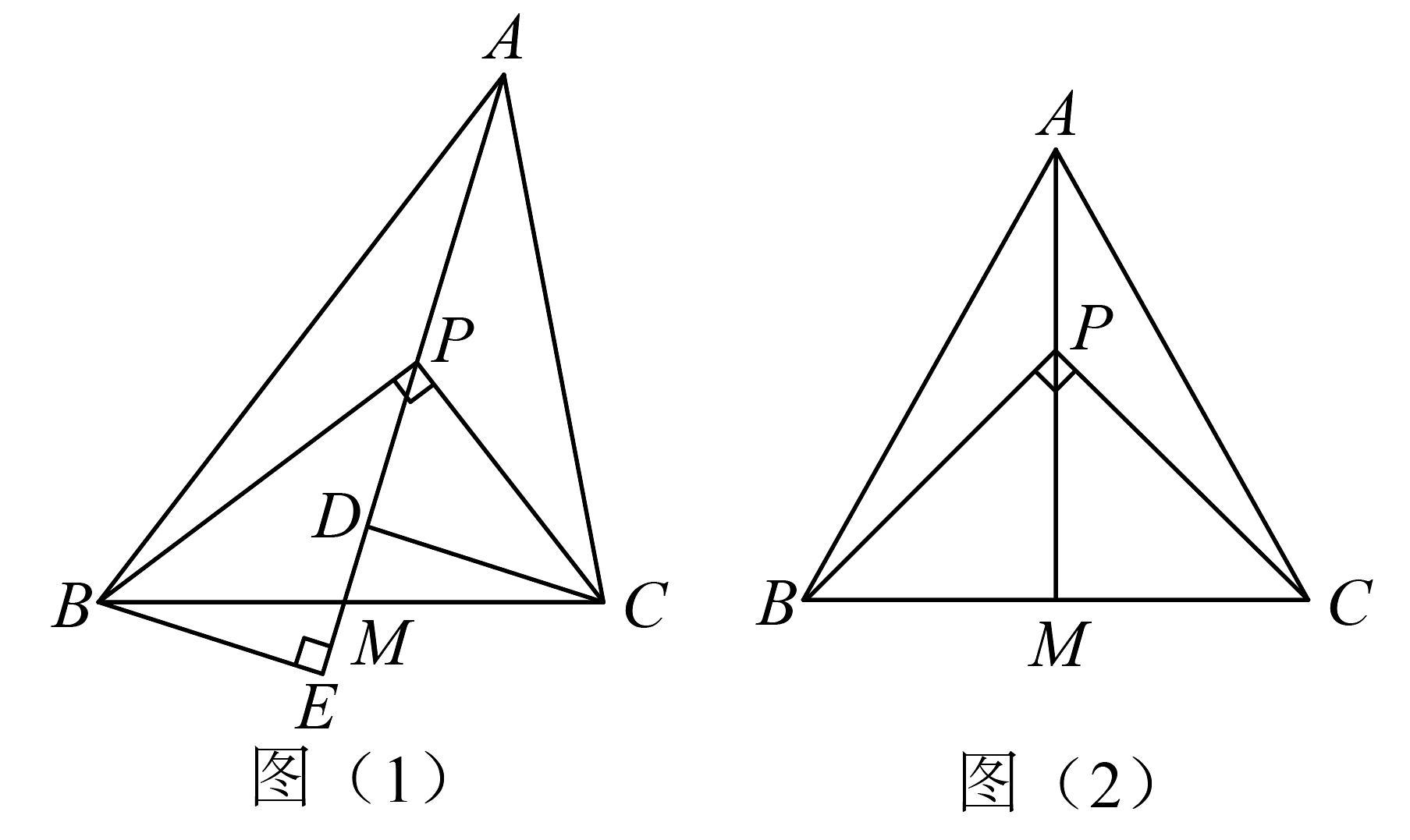 (1)、如图(1),过、分别作中线的垂线,垂足为、 . 求证: .(2)、①如图(2),当 , 且时, (填一个恰当的数).
(1)、如图(1),过、分别作中线的垂线,垂足为、 . 求证: .(2)、①如图(2),当 , 且时, (填一个恰当的数).②如图(1),当 , 为锐角三角形,且时,①中的结论还成立吗?若成立,请写出证明过程;若不成立,也请说明理由.