2.5 有理数的混合运算提升课时卷-北师大版数学七年级上册

试卷更新日期：2025-09-01 类型：同步测试

进入出卷网下载

一、选择题

1. 下列运算错误的是（）

A、 ${(- 3)}^{2} - (- 4) \div |- 2| = 9 + 4 \div 2$ B、 $2^{2} - {(- 1)}^{2023} = 4 + 1$ C、 $- 7 \div 2 \times (- \frac{1}{2}) = 7 \div 2 \times \frac{1}{2}$ D、 $\frac{7}{13} \times (- 9) + (- 3) \times (- \frac{7}{13}) - \frac{7}{13} \times 2 = \frac{7}{13} \times (- 9 - 3 + 2)$

查看试题解析
2. 若a、b、c、d为有理数，现规定一种新的运算为： $|\begin{matrix} a & b \\ c & d \end{matrix}| = a d - b c$ ，则 $|\begin{matrix} 6 & - 2 \\ 2 & - 1 \end{matrix}|$ 的结果是（）

A、 $- 2$ B、2 C、 $- 10$ D、10

查看试题解析
3. 三位同学在计算 $(\frac{1}{4} + \frac{1}{6} - \frac{1}{2}) \times 12$ 时，用了不同的方法：
小小说：12的 $\frac{1}{4}$ ， $\frac{1}{6}$ ， $\frac{1}{2}$ 分别是3，2和6，所以结果应该是 $3 + 2 - 6 = - 1$ ；
聪聪说：先计算括号里面的数， $\frac{1}{4} + \frac{1}{6} - \frac{1}{2} = - \frac{1}{12}$ ，再乘以12得到 $- 1$ ；
明明说：把12与 $\frac{1}{4}$ ， $\frac{1}{6}$ ， $- \frac{1}{2}$ 分别相乘后再相加，得到结果是 $- 1$ ．
对于三位同学的计算方式，下面描述正确的是（）

A、三位同学都用了运算律 B、聪聪使用了加法结合律 C、明明使用了乘法分配律 D、小小使用乘法交换律

查看试题解析
4. 在计算 $- 2^{2} + 5 \div (- 2) \times \frac{1}{2} - 9 \times (2 - \frac{1}{3} - \frac{2}{9})$ 时，有四位同学给出了以下四种计算步骤，其中正确的是（）

A、原式 $= 1 \div (- 2) \times \frac{1}{2} - 9 \times (2 - \frac{1}{3} - \frac{2}{9})$ B、原式 $= - 4 + 5 \div (- 1 - 9) \times (2 - \frac{1}{3} - \frac{2}{9})$ C、原式 $= - 4 + 5 \div (- 2) \times \frac{1}{2} - 18 + 3 + 2$ D、原式 $= 4 + 5 \div (- 2) \times \frac{1}{2} - 18 + 3 + 2$

查看试题解析
5. 规定新运算“@”：对于任意实数m ， n都有 m@n＝mn﹣m+n ，例如：2@3＝2×3﹣2+3．若2@（x﹣1）的运算结果与（x﹣1）@2的运算结果相同，则x的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 我国古代《易经》一书记载了一种“结绳计数”的方法，一女子在从右到左依次排列的绳子上打结，满七向左进一，用来记录采集到的野果数量，下列图示中，表示162颗的是（）

A、 B、 C、 D、

查看试题解析
7. 对于一个各数位上的数字均不为0的三位自然数N，若N能被它的各数位上的数字之和m整除，则称N是m的“和倍数”．对下列三个人的说法判断正确的是（　　）
小嘉说：247是13的“和倍数” 小淇说：441是9的“和倍数”
小华说：214、357均不是“和倍数”

A、三人说法都对 B、只有一人说法不对 C、小华说的不对 D、只有一人说法对

查看试题解析
8. 干支纪年法是中国自古以来就一直使用的纪年方法，干支是天干和地支的总称．干支纪年法的组合方式是天干在前，地支在后，以十天干和十二地支循环配合，每个组合代表一年，60年为一个循环．我们把天干、地支按顺序排列，且给它们编上序号．天干的计算方法是：年份减3，除以10所得的余数；地支的计算方法是：年份减3，除以12所得的余数．以2000年为例：天干为 $(2000 - 3) \div 10 = 199 \dots \dots 7$ ；地支为 $(2000 - 3) \div 12 = 166 \dots \dots 5$ ；对照天干地支表得出，2000年为农历庚辰年．

1
2
3
4
5
6
7
8
9
10
11
12
天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸

地支
子
丑
寅
卯
辰
巳
午
未
申
酉
戌
亥
依据上述规律推断2025年为农历（）年．

A、乙巳 B、戊申 C、乙申 D、戊巳

查看试题解析

二、填空题

9. 定义一种新运算： $a * b = a^{2} - 3 b$ ，则 $3 * (- 1) =$ ．

查看试题解析
10. 下表是10筐蔬菜的质量记录，每以20kg为标准质量（高于标准质量记为“+”），则这10筐蔬菜总质量为kg
筐数
2
3
1
2
2
与标准质量比较/kg
-0.8
+0.5
-0.5
+0.4
+0.5

查看试题解析
11. 2020年9月27日，从衢州开往福建宁德的铁路正式通车，途径松阳，是松阳开通的第一条火车线路，停靠如图所示的13个站点，不同的火车票一共需要设置种(注：往返的车票不同).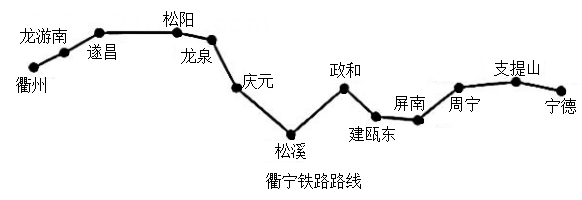

查看试题解析
12. 三个不等于零的有理数a，b，c满足（a+b)（b+c)（c+a)=0，则 $\frac{(a + b + c) (a^{3} + b^{3} + c^{3}) (a^{5} + b^{5} + c^{5}) (a^{7} + b^{7} + c^{7}) (a^{9} + b^{9} + c^{9})}{a^{25} + b^{25}}$ =.

查看试题解析
13. 对于正数x，规定 $f (x) = \frac{x}{1 + x} . 例如， f (2) = \frac{2}{1 + 2} = \frac{2}{3}, f (3) = \frac{3}{1 + 3} = \frac{3}{4}, f (\frac{1}{2}) = \frac{\frac{1}{2}}{1 + \frac{1}{2}} = \frac{1}{3}, f (\frac{1}{3}) = \frac{\frac{1}{3}}{1 + \frac{1}{3}} = \frac{1}{4}, \dots,$ 利用以上的规律计算： $f (\frac{1}{2024}) + f (\frac{1}{2023}) + f (\frac{1}{2022}) + f (\frac{1}{2021}) + \dots + f (\frac{1}{2}) + f (1) + f (2) + \dots + f (2021) + f (2022) + f (2023) + f (2024) =$ .

查看试题解析

三、解答题

14. 计算下列各题：

(1)、 $(- \frac{3}{4}) - (- \frac{1}{2}) + (- \frac{1}{4}) + (+ 8.5)$ .

(2)、 $- 1^{2022} + {(- 3)}^{2} \div \frac{1}{2} - | - 2 |$ .

(3)、 $(\frac{1}{4} - \frac{2}{3} - \frac{5}{6}) \times (- 12)$ .

(4)、 $(- 70) \times (- \frac{1}{4}) + 0.25 \times 12.5 + (- 17.5) \times (- 25 %)$ .

查看试题解析
15. 计算：

(1)、 $(- 12) - 5 + (- 14) - (- 39)$ ；

(2)、 $(- \frac{5}{6} + \frac{3}{8} - \frac{1}{4}) \times (- 24)$ ；

(3)、 $(- \frac{8}{3}) \div \frac{1}{9} \times (- \frac{5}{8}) \div (- 15)$ ；

(4)、 $- 1^{4} - \frac{1}{6} \times [2 - {(- 3)}^{2}]$ .

查看试题解析
16. 请先阅读下列内容，然后解答问题.
$∵ \frac{1}{1 \times 2} = 1 - \frac{1}{2}, \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}, \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}, \dots, \frac{1}{9 \times 10} = \frac{1}{9} - \frac{1}{10},$
$∴ \frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{9 \times 10}$
$= (1 - \frac{1}{2} + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + . \dots + (\frac{1}{9} - \frac{1}{10})$
$= 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \dots + \frac{1}{9} - \frac{1}{10}$
$= 1 - \frac{1}{10} = \frac{9}{10} .$
问题：
计算：

(1)、 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2024 \times 2025} .$

(2)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{49 \times 51}$

查看试题解析
17. 对于任意有理数a，b，定义运算：a⊙b=a(a+b)-1，等式右边是通常的加法、减法、乘法运算.例如，2⊙5=2×(2+5)-1=13.

(1)、求(1⊙2)⊙3 $\frac{1}{2} 的值；$

(2)、对于任意有理数m，n，请你重新定义一种运算“⊕”，使得5⊕3=20，写出你定义的运算：m⊕n=.(用含m，n的式子表示)

查看试题解析
18. 以下有5张数字卡片，请你按要求取出卡片，解决下列各问题：

(1)、从中取出2张卡片，使这2张卡片上数字乘积最大，最大值是

(2)、从中取出2张卡片，使这2张卡片上数字相除的商最小，最小值是

(3)、从中取出除0以外的其他4张卡片，将这4个数字进行加、减、乘、除或乘方混
合运算，使运算结果为 24（每个数字只能用一次），请写出两种符合要求的运算式子：
①②

查看试题解析
19. 佛手是金华市一大特产，现有10筐佛手，以每筐10千克为标准质量，超过或不足的千克数分别用正数、负数来表示，结果记录在下表：
与标准质量的差值(单位：千克)
-0.2
-0.15
0
0.3
筐数
1
2
4
3

(1)、这10筐佛手中，与标准质量的差值为-0.15千克的有筐，最重的一筐重千克。

(2)、若佛手每千克售价45元，则出售完这10筐佛手总收入多少元?

查看试题解析
20. 【概念探究】在学习了有理数的乘方运算后．小芳对类似于 $(- 5) \div (- 5) \div (- 5) \div (- 5)$ 这样几个相同有理数（均不等于0）的除法运算产生了兴趣，决定探究学习．经过查阅资料，类比有理数的乘方运算，小芳知道这种除法运算叫做除方，并把 $(- 5) \div (- 5) \div (- 5) \div (- 5)$ 记作 ${(- 5)}_{4}$ ，读作“ $- 5$ 的4次商”．
【概念归纳】一般地，我们把 $n$ 个 $a$ （ $a \neq 0$ ）相除记作 $a_{n}$ ，读作“ $a$ 的 $n$ 次商”

(1)、【概念理解】直接写出结果： ${(- 1)}_{3} =$ ．

(2)、关于除方，下列说法正确的是：（填序号）
①任何非零数的2次商都等于1；②对于任何正整数 $n$ ， ${(- 1)}_{n} = - 1$ ；③ $3_{4} = 4_{3}$ ；
④负数的奇数次商结果是负数，负数的偶数次商结果是正数

(3)、【概念运用】经过探究，小芳发现有理数的除方运算可转化为乘方运算，例： $3_{4} = 3 \div 3 \div 3 \div 3$ $= 3 \times \frac{1}{3} \times \frac{1}{3} \times \frac{1}{3} = {(\frac{1}{3})}^{2}$ ．仿照上面的算式，将下列运算结果直接写成乘方（幂）的形式：
${(- 5)}_{4} =$ ； ${(\frac{1}{3})}_{n} =$ ．

(4)、计算： $5_{2} \div {(- \frac{1}{3})}_{5} \times {(- \frac{1}{2})}_{3} + {(- \frac{1}{7})}_{3} \times \frac{1}{7}$ ．

查看试题解析
21. 类比有理数的乘方，我们定义“除方”运算，比如：2÷2÷2可记做2③，(-3)÷(-3)÷(-3)÷(-3)记做(-3)^④ ，一般地把n个a 相除记做 $a^{ⓝ}$ ，读做“a的圈n次方”.

(1)、直接写出计算结果： $2^{③}$ ； ${(- \frac{1}{2})}^{③} =$ .

(2)、我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，那么除方运算如何转化为乘方运算呢? 方法如下：
除方→2^④ =2÷2÷2÷2=2× $\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = {(\frac{1}{2})}^{2}$ →乘方的形式
仿照以上例子，把除方运算写乘方形式：（-3）^⑤= ， ${(\frac{1}{5})}^{⑥}$ =.
${(- \frac{1}{3})}^{3} 5^{4}$

(3)、算一算： $12^{2} \div {(- \frac{1}{3})}^{④} \times (- 2)^{⑥} - {(- \frac{1}{3})}^{⑥} \div 3^{3}$

查看试题解析

与标准质量的差值(单位：千克)	-0.2	-0.15	0	0.3
筐数	1	2	4	3

筐数	2	3	1	2	2
与标准质量比较/kg	-0.8	+0.5	-0.5	+0.4	+0.5