2.3 有理数的乘除运算提升课时卷-北师大版数学七年级上册

试卷更新日期：2025-09-01 类型：同步测试

进入出卷网下载

一、选择题

1. 下列说法正确的是 $($ $)$

A、非零两数的和一定大于任何一个加数 B、非零两数的差一定小于被减数 C、大于1的两数之积一定大于任何一个因数 D、小于1的两数之商一定小于被除数

查看试题解析
2. 算式（1.25+1.25+1.25+1.25）×25×8最简便的计算方法是（）

A、按顺序计算 B、（1.25×8）×（25×4） C、1.25×4×25×8 D、1.25×25×4×8

查看试题解析
3. 从 $- 6$ ， $- 4$ ， $- 1$ ， 7，5，a（ $|a| < 4$ ，且a为整数）这6个数中取其中3个不同的数作为因数，则它们积的最小值为（）

A、 $- 210$ B、 $- 35$ C、168 D、无法确定

查看试题解析
4. 如图，数轴上的点 $A$ ， $B$ 表示的数分别是 $a$ 、 $b$ ．如果 $a + b < 0$ ，且 $a b < 0$ ，那么该数轴的原点 $O$ 的位置应该在（）

A、点 $A$ 的左侧 B、点 $B$ 的右侧 C、点 $A$ 与点 $B$ 之间且靠近点 $A$ D、点 $A$ 与点 $B$ 之间且靠近点 $B$

查看试题解析
5. 把 $- 8$ 表示成两个整数的积，共出现的可能性有（　　）

A、2种 B、3种 C、4种 D、5种

查看试题解析
6. 某同学在计算 $(- 16) \div a$ 时，误将“ $\div$ ”看成“ $+$ ”，算出的结果是 $- 12$ ，则计算 $(- 16) \div a$ 的正确结果是（）

A、6 B、 $- 6$ C、4 D、 $- 4$

查看试题解析
7. 若 $a b < 0$ ，则 $\frac{2 | a |}{a} + \frac{3 b}{| b |}$ 的值可能是（　　）

A、 $\pm 5$ B、 $\pm 1$ C、1或5 D、 $\pm 1$ 或 $\pm 5$

查看试题解析
8. 已知： $C_{3}^{2} = \frac{3 \times 2}{1 \times 2} = 3 ， C_{5}^{3} = \frac{5 \times 4 \times 3}{1 \times 2 \times 3} = 10$ ， $C_{6}^{4} = \frac{6 \times 5 \times 4 \times 3}{1 \times 2 \times 3 \times 4} = 15$ $, \dots ，$ 观察上面的计算过程，利用规律计算 $C_{10}^{6}$ 的值为( )

A、42 B、210 C、840 D、2520

查看试题解析

二、填空题

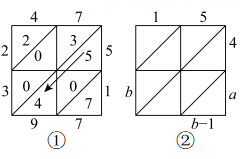
9. 若两个负整数的乘积是4，则这两个负整数的和为。

查看试题解析
10. 从 $- 3$ ， $- 2$ ， 0，3，5中任取三个数相乘，最大的值是．

查看试题解析
11. 如果 $|- m| = 5, |n| = 6$ ，那么 $- |m n| =$ ．

查看试题解析
12. 已知 $|x| = 6$ ， $|y| = \frac{1}{4}$ ，且 $x y > 0$ ， $x + y < 0$ ．则 $x - y =$ ．

查看试题解析
13. “格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出，在明代的《算法统宗》一书中被称为“铺地锦”.如图①，计算47×51，将乘数47计入上行，乘数51计入右行，然后以乘数47的每位数字乘乘数51的每位数字，将结果计入相应的格子中，最后按斜行加起来(斜行的和满十进一)，得2397.如图②，用“铺地锦”的方法表示两个两位数相乘，这两个两位数相乘的结果为.

查看试题解析

三、解答题

14. 计算

(1)、 $(- 8) \times 9 \times (- 1.25) \times (- \frac{1}{9})$

(2)、 $(- 36) \times (- \frac{4}{9} + \frac{5}{6} - \frac{7}{12})$

查看试题解析
15. 计算下列各题：

(1)、 $6.14 + (- 2 \frac{3}{4}) - (- 5.86) - \frac{1}{4}$ ；

(2)、 $\frac{2}{7} - 3 \frac{1}{3} + \frac{12}{7} - \frac{2}{3}$ ；

(3)、 $- 2.5 \times \frac{4}{5} \times (- \frac{5}{6}) \times \frac{3}{5}$ ；

(4)、 $(\frac{2}{3} - \frac{3}{4} + \frac{1}{6}) \times (- 24)$ ；

(5)、 $6.3 \times 0.125 + \frac{1}{8} \times 4.4 - \frac{1}{8} \times 0.7$ ．

查看试题解析
16. 外卖送餐为我们生活带来了许多便利，某学习小组调查了一名外卖小哥一周的送餐情况，规定送餐量超过 $50$ 单（送一次外卖称为一单）的部分记为“+”，低于 $50$ 单的部分记为“ $-$ ”，下表是该外卖小哥一周的送餐量：
星期
一
二
三
四
五
六
日
送餐量（单）
$- 4$
$+ 5$
$- 6$
$+ 16$
$- 8$
$+ 19$
$+ 27$

(1)、这七天中，送餐量最高的是星期，这天送餐单．

(2)、求该外卖小哥这一周平均每天送餐的单数．

(3)、外卖小哥每天的工资由底薪 $60$ 元加上送单补贴构成，送单补贴的方案如下：每天送餐量不超过 $50$ 单的部分，每单补贴2元；超过 $50$ 单但不超过 $60$ 单的部分，每单补贴4元；超过 $60$ 单的部分，每单补贴6元．求该外卖小哥这一周的工资收入．

查看试题解析
17. 某校举办了“废纸回收，变废为宝”活动，各班收集的废纸均以5kg为标准，超过的记为“＋”，不足的记为“-”，七年级六个班的废纸收集情况如表所示，统计员小虎不小心将一个数据弄脏看不清了，但他记得三班收集废纸最少，且收集废纸最多和最少的班级的质量差为 4 kg．
班级
一
二
三
四
五
六
超过（不足） $(kg)$
$+ 1$
$+ 2$
$- 1.5$
0
$- 1$

(1)、请你计算七年级六班同学收集废纸的质量．

(2)、若七年级计划总共收集废纸30kg，他们达到预期目标了吗?请说明理由．

(3)、若七年级六个班将本次活动收集的废纸集中卖出，30kg(包括30kg)以内的2元/kg，超出30kg的部分2.5 元kg，求废纸卖出的总钱数．

查看试题解析
18. 阅读下列内容，并回答相关问题：
小明说：“我定义了一种新的运算，叫(加乘)运算．”然后他写出了一些按照(加乘)运算的运算法则进行运算的算式：
(+4)※(+2)=+6；(-4)※(-3)=+7；
(-5)※(+3)=-8；(+6)※(-7)=-13；
(+8)※0=8；0※(-9)=9．
小亮看了这些算式后说：“我知道你定义的※(加乘)运算的运算法则了．”
你也明白了吗?

(1)、归纳※(加乘)运算的运算法则：
两数进行※(加乘)运算时，．
特别地，0和任何数进行※(加乘)运算，或任何数和0进行※(加乘)运算，．

(2)、计算：[(-2)※(+3)]※[(-12)※0]．(括号的作用与它在有理数运算中的作用一致)

(3)、我们知道加法有交换律和结合律，这两种运算律在有理数的※(加乘)运算中还适用吗?请你任选一个运算律，判断它在※(加乘)运算中是否适用，并举例验证．(举一个例子即可)

查看试题解析
19. 把几个数用大括号围起来，中间用逗号断开，如： $\{1, 2, - 3\} 、 \{- 2, 7, \frac{3}{4}, 19\},$ 我们称之为集合，其中的每个数称为该集合的元素.如果一个所有元素均为有理数的集合满足：当有理数a是集合的元素时，2015-a也必是这个集合的元素，这样的集合我们称为好的集合.例如集合{2015，0}就是一个好的集合.

(1)、集合{2015}好的集合，集合{-1，2016}好的集合(两空均填“是”或“不是”)；

(2)、若一个好的集合中最大的一个元素为4001，则该集合是否存在最小的元素?如果存在，请直接写出答案，否则说明理由；

(3)、若一个好的集合所有元素之和为整数M，且22161<M<22170，则该集合共有几个元素?说明你的理由.

查看试题解析
20. 根据以下素材，探究完成任务．
素材1：对于任何有理数 $x$ ，可用 $[x]$ 表示不超过 $x$ 的最大整数，如： $[- \frac{4}{3}] = - 2$ ，意思是数不超过 $- \frac{4}{3}$ 的最大整数是 $- 2$ ．
素材2：现对 $- 12$ 进行如下操作：取 $- 12$ 的三分之一，再取不超过它的最大整数，重复进行操作，即： $- 12 \overset{第一次}{\to} [\frac{- 12}{3}] = - 4 \overset{第二次}{\to} [\frac{- 4}{3}] = - 2 \overset{第三次}{\to} [\frac{- 2}{3}] = - 1$ ， $- 12$ 进行3次操作之后开始变为固定值 $- 1$ ．
任务1． $[\frac{5}{3}] =$ ______； $[- \frac{10}{3}] =$ ______．
任务2．任意整数 $n$ 进行3次操作，开始变为固定值 $- 1$ ，求 $n$ 取到的最大数和最小数．
任务3．任意整数 $n$ 进行3次操作，开始变为固定值0，请直接写出所有符合条件的数的和．

查看试题解析

星期	一	二	三	四	五	六	日
送餐量（单）	$- 4$	$+ 5$	$- 6$	$+ 16$	$- 8$	$+ 19$	$+ 27$

班级	一	二	三	四	五	六
超过（不足） $(kg)$	$+ 1$	$+ 2$	$- 1.5$	0	$- 1$