湖南省益阳市安化县第二中学2025届高三下学期5月模拟数学试题
试卷更新日期:2025-06-07 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
-
1. 已知集合 , 则( )A、 B、 C、 D、2. 已知i为虚数单位,若是实数,则实数( )A、 B、 C、1 D、23. 已知向量 , , 若 , 则( )A、2 B、1 C、-1 D、-24. 已知抛物线C:的焦点为F,点M在C上,若M到直线的距离为5,则( )A、4 B、5 C、6 D、75. 函数在内的零点之和为( )A、 B、 C、 D、06. 已知圆锥的母线长为 , 其外接球体积为 , 则该圆锥的表面积为( )A、3π B、6π C、9π D、12π7. 已知圆C:的一条直径的两个端点分别是A,B,则它们到直线l:的距离分别为 , , 则的最大值为( )A、16 B、32 C、48 D、648. 若函数有两个零点,则a的取值范围为( )A、 B、 C、 D、
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 某团队共有20人,他们的年龄分布如下表所示,
年龄
28
29
30
32
36
40
45
人数
1
3
3
5
4
3
1
有关这20人年龄的众数、极差、百分位数说法正确的有( )
A、众数是32 B、众数是5 C、极差是17 D、25%分位数是3010. 已知数列的首项为4,且满足 , 则( )A、为等差数列 B、为递增数列 C、的前项和 D、的前项和11. 如图,在直三棱柱中, , , 点M是线段上一点,则下列说法正确的是( )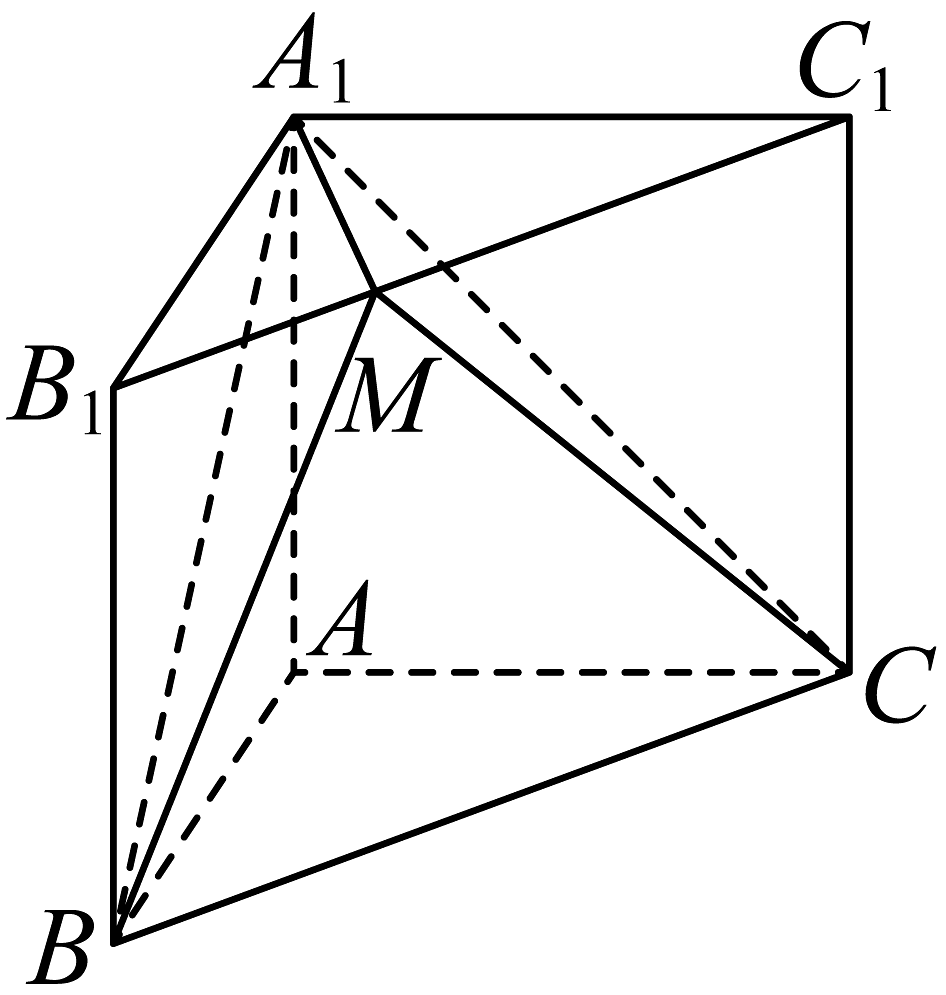 A、当M为的中点时,平面 B、四面体的体积为定值 C、的最小值为 D、四面体的外接球半径的取值范围是
A、当M为的中点时,平面 B、四面体的体积为定值 C、的最小值为 D、四面体的外接球半径的取值范围是三、填空题:本题共3小题,每小题5分,共15分.
-
12. 二项式的二项展开式中的常数项是 .13. 设实数 , , 使成立,则实数α的取值范围 .14. 已知数列满足 , 给出定义:使数列的前k项和为正整数的k()叫做好数,则在内的所有“好数”的和为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15. 如图,四棱锥中,底面 , , , , 平面PAD与平面PBC的交线为l,且 .
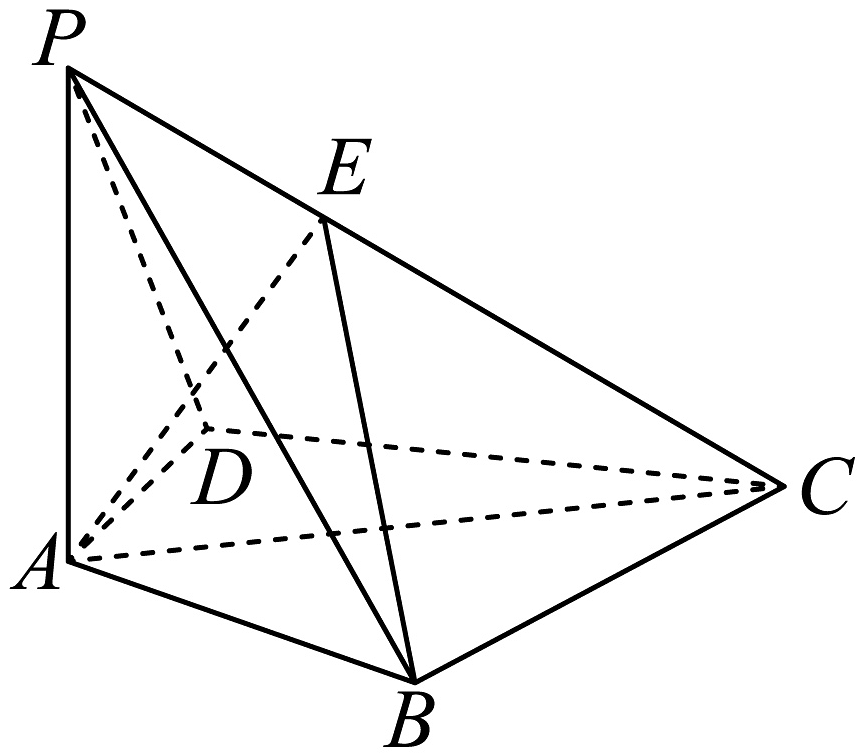 (1)、证明;(2)、若 , 求平面ABE与平面PCB夹角的余弦值.16. 在中,角所对的边分别为 , 已知 , 且 .(1)、若 , 求A;(2)、若是锐角三角形,求周长的取值范围.17. 已知函数 , 其中 .(1)、若在点处的切线与两坐标轴所围成三角形的面积为 , 求a的值;(2)、若是的极小值点,试比较与的大小.
(1)、证明;(2)、若 , 求平面ABE与平面PCB夹角的余弦值.16. 在中,角所对的边分别为 , 已知 , 且 .(1)、若 , 求A;(2)、若是锐角三角形,求周长的取值范围.17. 已知函数 , 其中 .(1)、若在点处的切线与两坐标轴所围成三角形的面积为 , 求a的值;(2)、若是的极小值点,试比较与的大小.