2025届江苏省盐城市建湖县第二中学高三三模数学试题
试卷更新日期:2025-04-27 类型:高考模拟
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. “ , 使”的一个充分不必要条件是( )A、 B、 C、 D、或2. 已知复数 , 则( )A、 B、 C、 D、3. 的奇偶性是( )A、偶函数 B、奇函数 C、既奇又偶函数 D、非奇非偶函数4. 如图,往一个正四棱台密闭容器内倒入的水,水面高度恰好为棱台高度的 , 且 , , 则这个容器的容积为( )
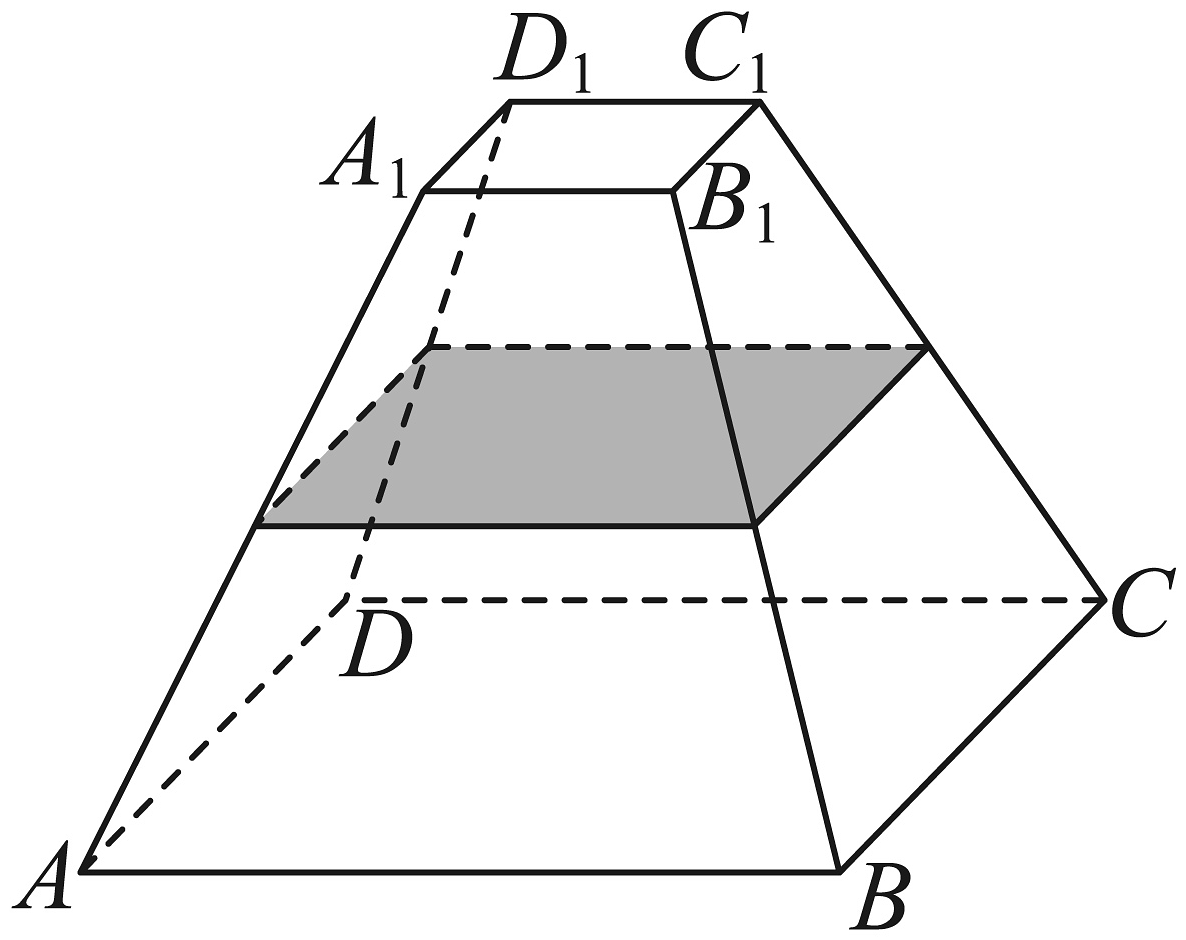 A、 B、 C、 D、5. 已知非零向量满足 , 向量在向量方向上的投影向量是 , 则与的夹角为( )A、 B、 C、 D、6. 已知过抛物线的焦点F且倾斜角为θ的直线l交C于A,B两点,O为坐标原点,若的面积为 , 则θ的值为( )A、 B、 C、或 D、或7. 在的展开式中含项的系数为15,则展开式中二项式系数最大的是第( )项A、2 B、3 C、4 D、58. 设曲线在处的切线与轴交点的横坐标为 , 则的值为( )A、 B、 C、 D、1
A、 B、 C、 D、5. 已知非零向量满足 , 向量在向量方向上的投影向量是 , 则与的夹角为( )A、 B、 C、 D、6. 已知过抛物线的焦点F且倾斜角为θ的直线l交C于A,B两点,O为坐标原点,若的面积为 , 则θ的值为( )A、 B、 C、或 D、或7. 在的展开式中含项的系数为15,则展开式中二项式系数最大的是第( )项A、2 B、3 C、4 D、58. 设曲线在处的切线与轴交点的横坐标为 , 则的值为( )A、 B、 C、 D、1二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
-
9. 已知某品牌汽车某年销量记录如下表所示:
月份x
1
2
3
4
5
6
销量y(万辆)
11.7
12.4
13.8
13.2
14.6
15.3
针对上表数据,下列说法正确的有( )
A、销量的极差为3.6 B、销量的60%分位数是13.2 C、销量的平均数与中位数相等 D、若销量关于月份的回归方程为 , 则10. 在中, , 则( )A、 B、的面积为8 C、 D、的内切圆半径是11. 已知数列的通项公式为 , 若数列是递减数列,则实数k不能取的值是( )A、 B、0 C、1 D、2三、填空题:本题共3小题,每小题5分,共15分.
-
12. 已知 , 则.13. 若随机事件、满足: , , , 则.14. 已知函数有三个零点,则实数的取值范围是.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤
-
15. 已知公差的等差数列的前n项的和为 , 且 , 成等比数列.(1)、求数列的通项公式;(2)、若数列满足 , 求数列的前n项的和.16. 已知函数 , 其中 .(1)、当时,求的图象在处的切线方程;(2)、若函数在区间上存在极值,求的取值范围.17. 如图,在三棱柱中,分别为的中点.
 (1)、证明:平面;(2)、若侧面底面 , 底面是等边三角形,侧面是菱形,且 , 求直线与侧面所成角的正弦值.18. 已知椭圆的离心率为 , 左、右顶点分别为A、B,左、右焦点分别为 . 过右焦点的直线l交椭圆于点M、N,且的周长为16.
(1)、证明:平面;(2)、若侧面底面 , 底面是等边三角形,侧面是菱形,且 , 求直线与侧面所成角的正弦值.18. 已知椭圆的离心率为 , 左、右顶点分别为A、B,左、右焦点分别为 . 过右焦点的直线l交椭圆于点M、N,且的周长为16. (1)、求椭圆C的标准方程;(2)、记直线AM、BN的斜率分别为 , 证明:为定值.19. 在中国诗词大会的比赛中,选手需要回答两组题展示自己的诗词储备.(1)、第一组题是情境共答题,参与比赛者需根据情境填写诗句.小王知道该诗句的概率是 , 且小王在不知道该诗句的情况下,答对的概率是.记事件A为“小王答对第一组题”,事件B为“小王知道该诗句”.
(1)、求椭圆C的标准方程;(2)、记直线AM、BN的斜率分别为 , 证明:为定值.19. 在中国诗词大会的比赛中,选手需要回答两组题展示自己的诗词储备.(1)、第一组题是情境共答题,参与比赛者需根据情境填写诗句.小王知道该诗句的概率是 , 且小王在不知道该诗句的情况下,答对的概率是.记事件A为“小王答对第一组题”,事件B为“小王知道该诗句”.(ⅰ)求小王答对第一组题的概率;
(ⅱ)在小王答对第一组题的情况下,求他知道该诗句的概率.
(2)、小王答对第一组题后开始答第二组题.第二组题为画中有诗,该环节共有三道题,每一题答题相互独立,但难度逐级上升,小王知道第n题的诗句的概率仍为 , 但是在不知道该诗句的情况下,答对的概率为 , 已知每一题答对的得分表如下(答错得分为0):题号
第1题
第2题
第3题
得分
2分
4分
6分
若获得8分及以上则挑战成功,求小王挑战成功的概率.