山东省济宁市2025届高考模拟考试(二模)数学试题
试卷更新日期:2025-04-27 类型:高考模拟
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知是关于的方程的一个根,则( )A、2 B、3 C、5 D、3. 已知圆锥的体积为 , 其侧面展开图是一个圆心角为的扇形,则该圆锥的底面半径为( )A、 B、1 C、 D、24. 若函数在上单调递减,则实数的取值范围是( )A、 B、 C、 D、5. 已知为等比数列,且 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 已知函数在区间上有且仅有3个零点,则实数的取值范围是( )A、 B、 C、 D、7. 若圆关于直线对称,其中 , , 则的最小值为( )A、2 B、 C、4 D、8. 已知是椭圆的右焦点,直线交于 , 两点,若 , 则椭圆的离心率为( )A、 B、 C、 D、
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对得部分分,有选错的得0分.
-
9. 已知 , 为随机事件,且 , , 则下列结论正确的是( )A、若 , 互斥,则 B、若 , 相互独立,则 C、若 , 相互独立,则 D、若 , 则10. 已知函数 , 则下列结论正确的是( )A、的图象关于轴对称 B、是的一个周期 C、在上为增函数 D、11. 已知正方体的棱长为1,点在正方体的内切球表面上运动,且满足平面 , 则下列结论正确的是( )A、 B、点的轨迹长度为 C、线段长度的最小值为 D、的最小值为
三、填空题:本题共3小题,每小题5分,共15分.
-
12. 已知函数则的值为.13. 已知抛物线的焦点为 , 为上的动点,点 , 则取最小值时,直线的斜率为.14. 箱子中装有4个红球,2个黄球(除颜色外完全相同),掷一枚质地均匀的骰子1次,如果点数为 , 则从该箱子中一次性取出个球.规定:依据个球中红球的个数,判定甲的得分 , 每一个红球记1分;依据个球中黄球的个数,判定乙的得分 , 每一个黄球记2分.比如:若一次性取出了2个红球,2个黄球,则判定甲得分 , 乙得分.则在1次掷骰子取球的游戏中,.
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.
-
15. 在中,内角 , , 所对的边分别为 , , , 且.(1)、证明:;(2)、若的面积为 , 证明为等边三角形.16. 如图,在四棱锥中,底面为矩形,为的中点, , .
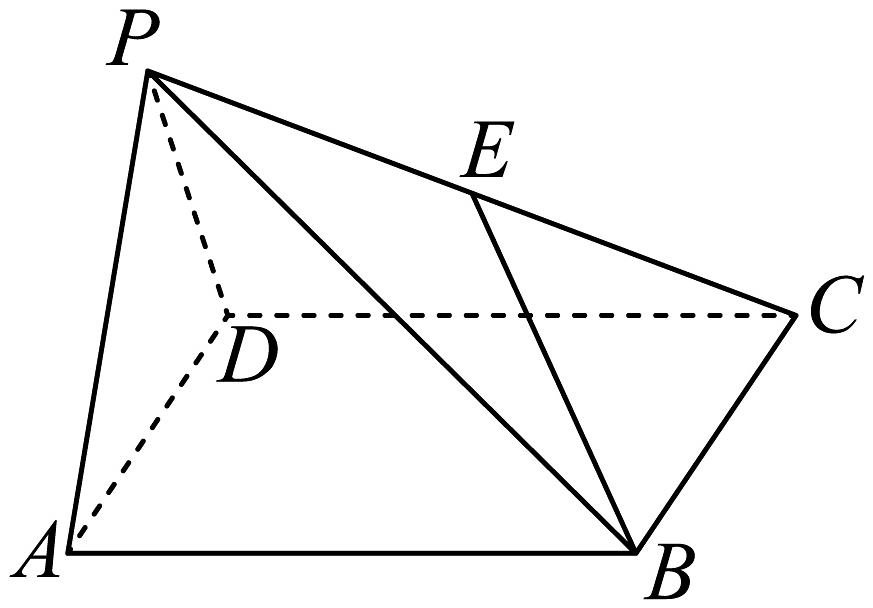 (1)、证明:平面平面;(2)、若 , 直线与平面所成角的正切值等于2,求平面与平面夹角的余弦值.17. 已知双曲线( , )的离心率为 , 且点在双曲线上,(1)、求的方程;(2)、若直线交于 , 两点,的平分线与轴垂直,求证:的倾斜角为定值.18. 已知函数 , .(1)、讨论零点的个数;(2)、若 , 求实数的取值范围.19. 将所有正整数按照如下规律形成数阵:
(1)、证明:平面平面;(2)、若 , 直线与平面所成角的正切值等于2,求平面与平面夹角的余弦值.17. 已知双曲线( , )的离心率为 , 且点在双曲线上,(1)、求的方程;(2)、若直线交于 , 两点,的平分线与轴垂直,求证:的倾斜角为定值.18. 已知函数 , .(1)、讨论零点的个数;(2)、若 , 求实数的取值范围.19. 将所有正整数按照如下规律形成数阵:第1行 1 2 3 …… 7 8 9
第2行 10 11 12 …… 97 98 99
第3行 100 101 102 …… 997 998 999
第4行 1000 1001 1002 …… 9997 9998 9999
…………
(1)、将数列与数列的公共项按照从小到大的顺序排列得到数列 , 试确定在该数阵中的位置;(2)、将数阵中所有相邻两位数字(从左到右)出现12的所有正整数去掉并保持顺序不变,得到一个新数阵,记新数阵第行中正整数的个数为.(i)求 , , ;
(ii)求.