备考2018年高考数学一轮基础复习：专题9 推理与证明、算法、复数

试卷更新日期：2017-12-11 类型：一轮复习

进入出卷网下载

一、单选题

1. 为提高信息在传输中的抗干扰能力，通常在原信息中按一定规则加入相关数据组成传输信息，设定原信息为a₀a₁a₂ ， a_i∈{0，1}（i=0，1，2），传输信息为h₀a₀a₁a₂h₁ ，其中h₀=a₀⊕a₁ ， h₁=h₀⊕a₂ ． ⊕运算规则为：0⊕0=0，0⊕1=1，1⊕0=1，1⊕1=0，例如原信息为111，则传输信息为01111．传输信息在传输过程中受到干扰可能导致接收信息出错，则下列接收信息一定有误的是（）

A、10111 B、01100 C、11010 D、00011

查看试题解析
2. 若复数 $\frac{a + 3 i}{1 + 2 i}$ （a∈R，i为虚数单位位）是纯虚数，则实数a的值为（）

A、﹣2 B、4 C、﹣6 D、6

查看试题解析
3. 用数学归纳法证明“1+ $\frac{1}{2}$ + $\frac{1}{3}$ +…+ $\frac{1}{2^{n} - 1}$ ＜n（n∈N^* ， n＞1）”时，由n=k（k＞1）不等式成立，推证n=k+1时，左边应增加的项数是（　　）

A、2^k^﹣1 B、2^k﹣1 C、2^k D、2^k+1

查看试题解析
4. 若X是一个集合，τ是一个以X的某些子集为元素的集合，且满足：
①X属于τ，ϕ属于τ；
②τ中任意多个元素的并集属于τ；
③τ中任意多个元素的交集属于τ．则称τ是集合X上的一个拓扑．
已知集合X={a，b，c}，对于下面给出的四个集合τ：
①τ={∅，{a}，{c}，{a，b，c}}；
②τ={∅，{b}，{c}，{b，c}，{a，b，c}}；
③τ={∅，{a}，{a，b}，{a，c}}；
④τ={∅，{a，c}，{b，c}，{c}，{a，b，c}}．
其中是集合X上的拓扑的集合τ的序号是（　　）

A、① B、② C、②③ D、②④

查看试题解析
5. 《聊斋志异》中有这样一首诗：“挑水砍柴不堪苦，请归但求穿墙术．得诀自诩无所阻，额上坟起终不悟．”在这里，我们称形如以下形式的等式具有“穿墙术”：
2 $\sqrt{\frac{2}{3}}$ = $\sqrt{2 \frac{2}{3}}$ ，3 $\sqrt{\frac{3}{8}}$ = $\sqrt{3 \frac{3}{8}}$ ，4 $\sqrt{\frac{4}{15}}$ = $\sqrt{4 \frac{4}{15}}$ ，5 $\sqrt{\frac{5}{24}}$ = $\sqrt{5 \frac{5}{24}}$
则按照以上规律，若8 $\sqrt{\frac{8}{n}}$ = $\sqrt{8 \frac{8}{n}}$ 具有“穿墙术”，则n=（）

A、7 B、35 C、48 D、63

查看试题解析
6. 执行如图所示的程序框图，若输出的S的值为64，则判断框内可填入的条件是（）

A、k≤3？ B、k＜3？ C、k≤4？ D、k＞4？

查看试题解析
7. 我国古代数学名著《九章算术》的论割圆术中有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”它体现了一种无限与有限的转化过程．比如在表达式1+ $\frac{1}{1 + \frac{1}{1 + \dots}}$ 中“…”即代表无数次重复，但原式却是个定值，它可以通过方程1+ $\frac{1}{x}$ =x求得x= $\frac{\sqrt{5} + 1}{2}$ ．类比上述过程，则 $\sqrt{3 + 2 \sqrt{3 + 2 \sqrt{\dots}}}$ =（）

A、3 B、 $\frac{\sqrt{13} + 1}{2}$ C、6 D、2 $\sqrt{2}$

查看试题解析
8. 观察下列各式：5⁵=3 125，5⁶=15 625，5⁷=78 125，…，则5²⁰¹⁷的末四位数字为（）

A、3 125 B、5 625 C、8 125 D、0 625

查看试题解析
9. 要证：a²+b²﹣1﹣a²b²≤0，只要证明（　　）

A、2ab﹣1﹣a²b²≤0 B、a²+b²﹣1﹣ $\frac{a^{4} + b^{4}}{2}$ ≤0 C、 $\frac{a + b^{2}}{2}$ ﹣1﹣a²b²≤0 D、（a²﹣1）（b²﹣1）≥0

查看试题解析
10. 定义某种运算S=a⊗b，运算原理如图所示，则式子[（2tan $\frac{13 π}{4}$ ）⊗lg $\frac{1}{10}$ ]+[lne⊗（ $\frac{1}{5}$ ）^﹣¹]的值为（）

A、4 B、8 C、10 D、13

查看试题解析
11. 阅读如图所示的程序框图，则该算法的功能是（）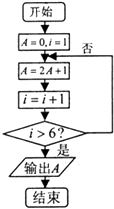

A、计算数列{2ⁿ^﹣¹}前5项的和 B、计算数列{2ⁿ﹣1}前5项的和 C、计算数列{2ⁿ^﹣¹}前6项的和 D、计算数列{2ⁿ﹣1}前6项的和

查看试题解析

二、填空题

12. 对正整数m的3次幂有如下分解方式：
1³=1 2³=3+5 3³=7+9+11 4³=13+15+17+19
根据上述分解规律，则10³的分解中最大的数是．

查看试题解析
13. 复数 $z = \frac{3 - i}{i + 2}$ 在复平面内对应的点位于第象限．

查看试题解析
14. 我国古代数学名著《张邱建算经》有“分钱问题”：今有与人钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱，与讫，还敛聚与均分之，人得一百钱，问人几何？意思是：将钱分给若干人，第一人给3钱，第二人给4钱，第三人给5钱，以此类推，每人比前一人多给1钱，分完后，再把钱收回平均分给各人，结果每人分得100钱，问有多少人？则题中的人数是．

查看试题解析
15. 如图程序框图运行后，如果输出的函数值在区间[﹣2， $\frac{1}{2}$ ]内，则输入的实数x的取值范围是．

查看试题解析

三、综合题

16. 阅读材料：根据两角和与差的正弦公式，有：
sin（α+β）=sinαcosβ+cosαsinβ﹣﹣﹣﹣﹣﹣①
sin（α﹣β）=sinαcosβ﹣cosαsinβ﹣﹣﹣﹣﹣﹣②
由①+②得sin（α+β）+sin（α﹣β）=2sinαcosβ﹣﹣﹣﹣﹣﹣③
令α+β=A，α﹣β=β　有α= $\frac{A + B}{2}$ ，β= $\frac{A - B}{2}$ 代入③得　sinA+sinB=2sin $\frac{A + B}{2}$ cos $\frac{A - B}{2}$ ．

(1)、利用上述结论，试求sin15°+sin75°的值；

(2)、类比上述推证方法，根据两角和与差的余弦公式，证明：cosA﹣cosB=﹣2sin $\frac{A + B}{2}$ cos $\frac{A - B}{2}$ ．

查看试题解析
17. 已知复数z=bi（b∈R）， $\frac{z - 2}{1 + i}$ 是实数，i是虚数单位．

(1)、求复数z；

(2)、若复数（m+z）²所表示的点在第一象限，求实数m的取值范围．

查看试题解析
18. 设复平面上点Z₁ ， Z₂ ， …，Z_n ， …分别对应复数z₁ ， z₂ ， …，z_n ， …；

(1)、设z=r（cosα+isinα），（r＞0，α∈R），用数学归纳法证明：zⁿ=rⁿ（cosnα+isinnα），n∈Z⁺

(2)、已知 $z_{1} = {(\frac{1 + i}{1 - i})}^{20}$ ，且 $\frac{z_{n + 1}}{z_{n}} = \frac{1}{2}$ （cosα+isinα）（α为实常数），求出数列{z_n}的通项公式；

(3)、在（2）的条件下，求 $L = | \vec{Z_{1} Z_{2}} | + | \vec{Z_{2} Z_{3}} | + \dots + | \vec{Z_{n} Z_{n + 1}}$ |+…．

查看试题解析

四、解答题

19. 已知n∈N^* ， S_n=（n+1）（n+2）…（n+n）， $T_{n} = 2^{n} \times 1 \times 3 \times \dots \times (2 n - 1)$ ．
（Ⅰ）求 S₁ ， S₂ ， S₃ ， T₁ ， T₂ ， T₃；
（Ⅱ）猜想S_n与T_n的关系，并用数学归纳法证明．

查看试题解析
20. 按如图所示的程序框图操作：
（Ⅰ）写出输出的数所组成的数集．若将输出的数按照输出的顺序从前往后依次排列，则得到数列{a_n}，请写出数列{a_n}的通项公式；
（Ⅱ）如何变更A框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列{2n}的前7项？
（Ⅲ）如何变更B框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项？

查看试题解析
21. 已知数集A={a₁ ， a₂ ， …，a_n}（1=a₁＜a₂＜…＜a_n ， n≥4）具有性质P：对任意的k（2≤k≤n），∃i，j（1≤i≤j≤n），使得a_k=a_i+a_j成立．
（Ⅰ）分别判断数集{1，2，4，6}与{1，3，4，7}是否具有性质P，并说明理由；
（Ⅱ）求证：a₄≤2a₁+a₂+a₃；
（Ⅲ）若a_n=72，求n的最小值．

查看试题解析