专题18 项目式实践——中考数学新考法靶向训练-在线组卷题库

1. 项目化学习

项目主题：为学校图书馆设计无障碍通道．

项目背景：2023年6月28日，我国颁布《中华人民共和国无障碍环境建设法》．某校“综合与实践”小组以“为学校图书馆设计无障碍通道”为主题展开项目学习．

研究步骤：（1）查阅资料得知，无障碍通道有三种类型：直线形、直角形、折返形；

（2）实地测量图书馆门口场地的大小；

（3）为了方便师生出入图书馆，并尽量减少通道对师生其它通行的影响，研讨认为设计折返形无障碍通道比较合适．

设计方案：“综合与实践”小组为该校图书馆设计的无障碍通道如图2所示，其中 $M N$ 为地面所在水平线， $C D$ 和 $D F$ 是无障碍通道，并且 $∠ C D F = 2 ∠ D F E$ ，立柱 $C G$ ， $D E$ 均垂直于地面， $G E = 6$ 米， $F E = 4$ 米．

解决问题：若原台阶坡道的长度（线段 $A B$ 的长度）为5米，坡角 $α$ 的度数为 $23 °$ ， $B C ∥ M N$ ，求出无障碍通道的总长（线段 $C D$ 和 $D F$ 的和）为多少米？（结果保留根号．参考数据： $\sin 23 ° \approx 0.40$ ， $\cos 23 ° \approx 0.92$ ， $\tan 23 ° \approx 0.42$ ）

查看试题解析

2. 【项目式学习】

【项目主题】如何调整电梯球、落叶球的发球方向.

【项目素材】

素材一，如图1是某足球场的一部分，球门宽 $D E = C F = 7 m$ ，高 $C D = E F = 2.51 m$ ，小梅站在A处向门柱 $C D$ 一侧发球，点A正对门柱 $C D$ （即 $A C ⊥ C F$ ）， $A C = 24 m$ ，足球运动的路线是抛物线的一部分．

素材二，如图，当足球运动到最高点Q时，高度为 $4.5 m$ ，即 $Q B = 4.5 m$ ，此时水平距离 $A B = 15 m$ ，以点A为原点，直线 $B A$ 为x轴，建立平面直角坐标系．

【项目任务】

任务一：足球运动的高度 $y (m)$ 与水平距离 $x (m)$ 之间的函数关系式，此时足球能否入网？

任务二：改变发球方向，发球时起点不变，运动路线的形状不变，足球是否能打到远角E处再入网？

上述任务1、任务2中球落在门柱边线视同球入网；根据以上素材，探索完成任务.

查看试题解析

3. 某校项目式学习小组开展项目活动，过程如下：

项目主题：测量学校旗杆高度

问题驱动：能利用哪些科学原理来测量旗杆的高度？

组内探究：由于旗杆较高，需要借助一些工具来测量，例如自制直角三角形硬纸板，标杆，平面镜，甚至还可以利用无人机 $\dots$ 确定方法后，先画出测量示意图，然后实地进行测量，并得到具体数据，从而计算旗杆的高度．

成果展示：下面是同学们进行交流展示时的部分测量方案：

	方案一		方案二		$\dots$
测量工具	自制直角三角形硬纸板，皮尺		标杆，皮尺		$\dots$
测量示意图及说明	说明：线段 $A B$ 表示学校旗杆，小亮的眼睛到地面的距离 $C D = 1.7 m$ ，点 $D$ 与点 $B$ 在同一水平直线上， $D$ ， $B$ 之间的距离可以直接测得，且 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ ， $G$ 都在同一竖直平面内， $A$ ， $C$ ， $E$ 三点在同一直线上， $C$ ， $F$ ， $G$ 三点在同一直线上		说明：线段 $A B$ 表示学校旗杆，小明的眼睛到地面的距离 $C D = 1.7 m$ ，标杆竖立位置点 $F$ 与点 $B$ ， $D$ 在同一水平直线上， $D$ ， $F$ ， $B$ 之间的距离都可以直接测得，且 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ 都在同一竖直平面内， $A$ ， $C$ ， $E$ 三点在同一直线上．
测量数据	$D$ ， $B$ 之间的距离	$16.8 m$	$D$ ， $B$ 之间的距离	$16.8 m$	$\dots$
	$E F$ 的长度	$0.50 m$	$D$ ， $F$ 之间的距离	$1.35 m$
	$C E$ 的长度	$0.75 m$	标杆 $E F$ 的长度	$2.60 m$
$\dots$	$\dots$

根据上述材料，请你选择一个方案，求出学校旗杆 $A B$ 的高度．

查看试题解析

4. 【项目式学习】

项目主题：如何拟定运动员拍照记录的方案？

项目背景：

(1)、任务一：确定滑道的形状

图1是单板滑雪运动员从大跳台滑雪场地滑出的场景，图2是跳台滑雪场地的横截面示意图．AC垂直于水平底面BC，点D到A之间的滑道呈抛物线型，已知 $A C = 3$ m， $B C = 4$ m，且点B处于跳台滑道的最低处，在图2中建立适当的平面直角坐标系，求滑道所在抛物线的函数表达式．

(2)、任务二：确定运动员达到最高点的位置

如图3，某运动员从点A滑出后的路径满足以下条件：

①运动员滑出路径与D、A之间的抛物线形状相同，

②该运动员在底面BC上方竖直距离9.75m处达到最高点P

③落点Q在底面BC下方竖直距离2.25m．

在同一平面直角坐标系中，求运动员到达最高处时与点A的水平距离．

(3)、任务三：确定拍摄俯角

α

高速摄像机能高度还原运动员的精彩瞬间，如图4，有一台摄像机M进行跟踪拍摄：

①它与点B位于同一高度，且与点B距离25.5m；

②运动过程需在摄像头视角范围内才能记录，记摄像头的俯角为 $α$ ；

③在平面直角坐标系中，设射线MN的解析式为 $y = k x + b (k \neq 0)$ ，其比例系数k和俯角 $α$ 的函数关系如图5所示．

若要求运动员的落点Q必须在摄像机M的视角范围内，则俯角 $α$ 至少多少度（精确到个位）？

查看试题解析

5. 【项目式学习】

项目主题：安全用电，防患未然．

项目背景：近年来，随着电动自行车保有量不断增多，火灾风险持续上升，据悉，约 $80 %$ 的火灾都在充电时发生，某校九年级数学创新小组，开展以“安全用电，防患未然”为主题的项目式学习，对电动自行车充电车棚的消防设备进行研究．

(1)、图1悬挂的是8公斤干粉灭火器，图2为其喷射截面示意图，在

△ A O B

中，

O A = O B

，喷射角

∠ A O B = 60 °

，地面有效保护直径

A B

为

2 \sqrt{3}

米，喷嘴

O

距离地面的高度

O C

为米；

(2)、任务二：模型构建

由于干粉灭火器只能扑灭明火，并不能扑灭电池内部的燃烧，在火灾发生时需要大量的水持续给电池降温，才能保证电池内部自燃熄灭，不会复燃．学校考虑给新建的电动自行车充电车棚安装消防喷淋头．

如图3，喷淋头喷洒的水柱最外层的形状为抛物线．已知学校的停车棚左侧靠墙建造，其截面示意图为矩形 $O A B C$ ，创新小组以点 $O$ 为坐标原点，墙面 $O A$ 所在直线为 $y$ 轴，建立如图4所示的平面直角坐标系．他们查阅资料后，提议消防喷淋头 $M$ 安装在离地高度为3米，距离墙面水平距离为2米处，即 $O A = 3$ 米， $A M = 2$ 米，水喷射到墙面 $D$ 处，且 $O D = 1$ 米．

①求该水柱外层所在抛物线的函数解析式；

②按照此安装方式，喷淋头 $M$ 的地面有效保护直径 $O E$ 为 ▲ 米；

(3)、任务三：问题解决

已知充电车棚宽度 $O C$ 为7米，电动车电池的离地高度为0.2米，创新小组想在喷淋头 $M$ 的同一水平线 $A B$ 上加装一个喷淋头 $N$ ，使消防喷淋头喷洒的水柱可以覆盖所有电动车电池，喷淋头 $N$ 距离喷淋头 $M$ 至少米．

查看试题解析

6. 【项目式学习】

项目主题：合理设计智慧泉源

项目背景：为加强校园文化建设，学校计划在原有的喷泉池内增设一块矩形区域，安装LED发光地砖灯，用于展示校园文化标语，要求该矩形区域被喷泉喷出水柱完全覆盖，因此需要对原有喷泉的喷头竖直高度进行合理调整，围绕这个问题，某数学学习小组开展了“合理设计智慧泉源”为主题的项目式学习，

(1)、任务一 测量建模

如图1，在水平地面上的喷泉池中心有一个可以竖直升降的喷头，它向四周喷出的水柱为抛物线.经过测量，水柱的落点均在水平地面半径为2米的圆上，在距池中心水平距离 0.75米处，水柱达到最高，高度为1.25米，学习小组根据喷泉的实景进行抽象，以池中心为原点，水平方向为x 轴，竖直方向为y轴建立平面直角坐标系，画出如图12 所示的函数图象，求水柱所在抛物线(第一象限部分)的函数表达式(不需写自变量的取值范围)：

(2)、任务二 推理分析

学习小组通过进一步分析发现：当喷头竖直高度调整时，喷头喷出的水柱抛物线形状不发生改变，当喷头竖直高度增加h米，水柱落点形成的圆半径相应增加d米，h与d之间存在一定的数量关系，求出h与d之间的数量关系式；

(3)、任务三 设计方案

现计划在原有喷水池内增设一块矩形区域ABCD，AB=1.4米，BC=0.4米，增设后的俯视图如图3所示，AB与原水柱落点形成的圆相切，切点为AB的中点P.若要求增设的矩形区域ABCD被喷泉喷出水柱完全覆盖，则喷头竖直高度至少应该增加米.

查看试题解析

7. 【项目式学习】

项目主题：守护生命，“数”说安全．

项目背景：随着社会的发展，安全问题变得日益重要．某校为了提高学生的安全意识，开展以“守护生命，'数'说安全”为主题的项目式学习活动．创新小组通过考察测量、模拟探究和成果迁移等环节，开展地下弯道对通行车辆长度的限制研究．

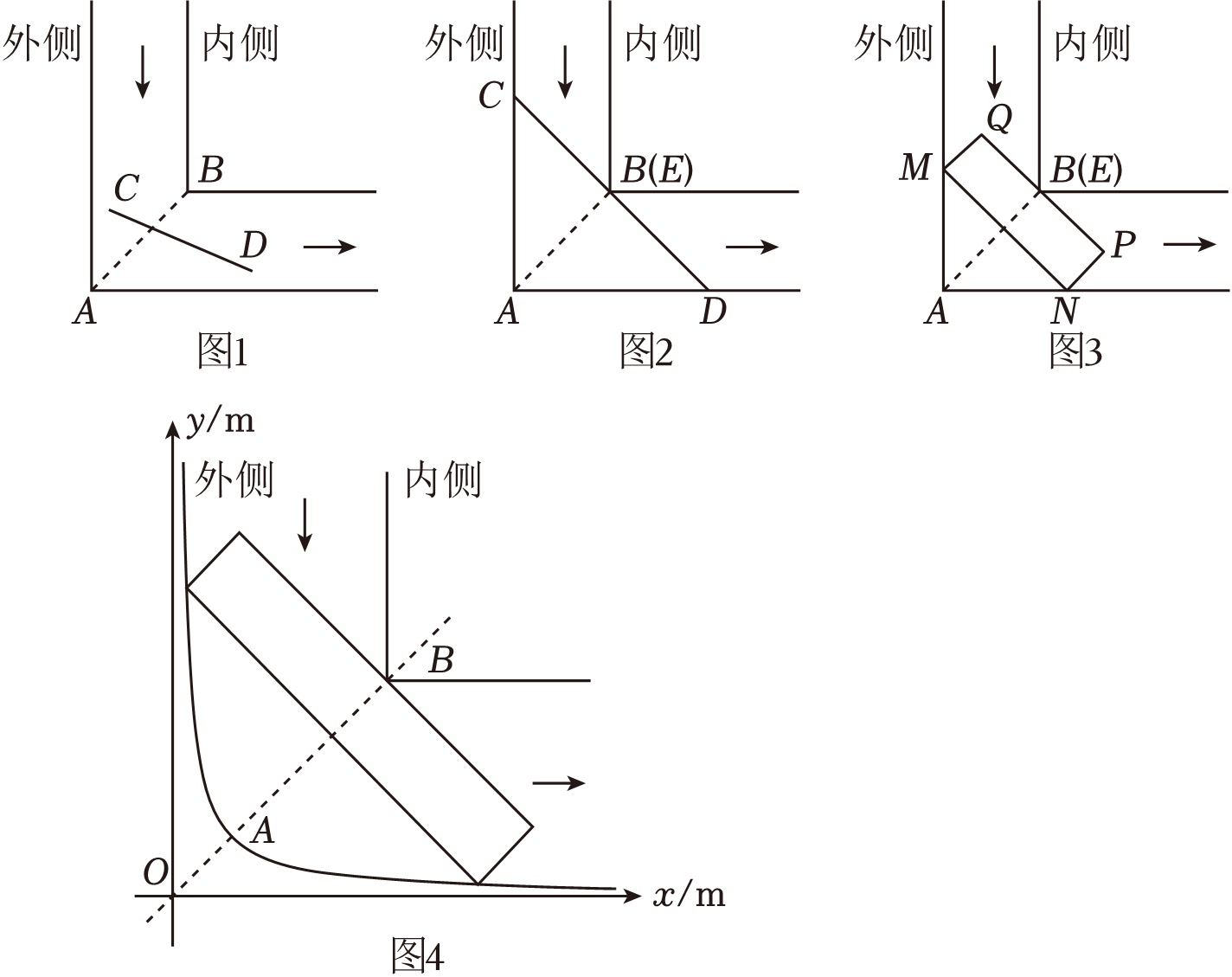
(1)、任务一：考察测量

如图1，创新小组所选取弯道的内、外侧均为直角，道路宽均为4m，则AB＝m；

(2)、任务二：模拟探究

如果汽车在行驶中与弯道内、外侧均无接触，则可安全通过．

创新小组用线段模拟汽车通过宽度相同的直角弯道，探究发现：

①当CD＜2AB时（如图1），线段CD能通过直角弯道；

②当CD＝2AB时，必然存在线段CD的中点E与点B重合的情况，线段CD恰好不能通过直角弯道（如图2）．此时，∠ADC的度数是；③当CD＞2AB时，线段CD不能通过直角弯道．

(3)、如图3，创新小组用矩形PQMN模拟汽车通过宽均为4m的直角弯道，发现当PQ的中点E与点B重合，且PQ⊥AB时，矩形PQMN恰好不能通过该弯道．若PQ＝am，PN＝2m，且矩形PQMN能通过该直角弯道，求a的最大整数值．

(4)、任务三：成果迁移

如图4，某弯道外侧形状可近似看成反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象，其对称轴交图象于点A．弯道内侧的顶点B在射线OA上，两边分别与x轴，y轴平行，OA＝2m，AB＝4 $\sqrt{2}$ m．创新小组探究发现通过该弯道的原理与通过直角弯道类似．有一辆长为bm，宽为2m的汽车需要安全通过该弯道，则b的最大整数值为．（参考数据： $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7， $\sqrt{5}$ ≈2.2， $\sqrt{7}$ ≈2.6）

查看试题解析

8. 影子在我们生活中是常见的，那么利用影子能解决什么问题呢?某校以《影子的故事》展开项目式学习：

(1)、地球有多大？2000多年前，古希腊数学家埃拉托斯特尼（Eratosthenes）利用太阳光线测量出了地球子午线的周长．

项目任务（一）

如图1，太阳光线 $A B / / C D, C E$ 是竖直插在球面上的木杆，AB、CE的延长线都经过圆心 $O$ ．已知B、E间的劣弧长约为800千米，子午线周长约为40000千米，则 $∠ D C E$ 的度数为 ▲ .

(2)、中国古代也有类似的记载，陈子测日法是由我国古代杰出的数学家陈子提出，用来测量太阳高度的．陈子测量太阳高度的方法可叙述为︰当夏至太阳直射北回归线时，在北方立一八尺高的标竿，观其影长为六尺。然后测量者向南移动标竿，每移动一千里，标竿的影长就减少一寸。查阅资料后，进行如下项目式研究：

项目任务（二）

如图2，某日正午，小红和小明在同一子午线的B地、C地测得太阳光与木棍的夹角分别为α，β，则∠BOA＝ ▲ ，若测得AB之间弧长为l，则地球子午线周长为 ▲ ．（用含α，β，l的代数式表示）

项目任务（三）

如图3，日落时，身高为h的小亮趴在地上平视远方，在太阳完全从地平线上消失的一瞬间，按下秒表开始计时．同时马上站起来，当太阳再次完全消失在地平线的瞬间，停止计时，小亮利用这个时间差和地球自转的速度计算出了∠PQH＝θ，请据此计算出地球的半径R= ▲ ．（用含h，θ的代数式表示）

项目任务（四）

如图，同学们发现校门旁边有一根电线杆AB和一块半圆形广告牌，在太阳光照射下，电线杆的顶端A的影子刚好落在半圆形广告牌的最高处G，而半圆形广告牌的影子刚好落在地面上一点E，通过测量得到BC＝5米，DE＝2米，并测得光线与水平面夹角∠DEF＝43°．请你利用同学们的测量数据求出电线杆AB的高度．（参考数据：sin43°≈0.68，cos43°≈0.73，tan43°≈0.93；结果保留整数）

查看试题解析

9. 地球有多大？古希腊数学家埃拉托斯特尼利用太阳光线测量出了地球子午线的周长．

下面让我们一起开启“探求地球周长”的数学项目化学习之旅．

项目任务(一)	如图 1，某日正午，小红在 $B$ 地 (与太阳直射点 $A$ 在同一子午线上)测得太阳光与木棍的夹角为 $α$ ，则 $∠ A O B =$ ▲ ．若测得 $A B$ 之间弧长为 $l$ ，则地球子午线周长为 ▲ (用含 $α ， l$ 的代数式表示)
项目任务(二)	如图 2 ，某日正午，小红和小明在同一子午线的 $B$ 地、 $C$ 地测得太阳光与木棍的夹角分别为 $α ， β$ ，则 $∠ B O C =$ ▲ ．若测得 $B C$ 之间弧长为 $l$ ，则地球子午线周长为 ▲ (用含 $α ， β ， l$ 的代数式表示)
项目任务(三)	如图 3 ，日落时，身高为 $h$ 的小亮蹲在地上平视远方，在太阳完全从地平线上消失的一瞬间，按下秒表开始计时．同时，他马上站起来，当太阳再次完全消失在地平线的瞬间，停止计时．小亮利用这个时间差和地球自转的速度计算出了 $∠ P Q H = θ$ ，请据此计算出地球的半径与周长．(用含 $h ， θ$ 的代数式表示)

查看试题解析

10. 【项目化学习】

项目主题：从函数角度重新认识“阻力对物体运动的影响”．

项目内容：数学兴趣小组对一个静止的小球从斜坡滚下后，在水平木板上运动的速度、距离与时间的关系进行了深入探究，兴趣小组先设计方案，再进行测量，然后根据所测量的数据进行分析，并进一步应用。

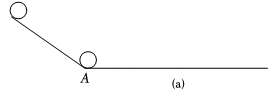
实验过程：如图（a）所示，一个黑球从斜坡顶端由静止滚下沿水平木板直线运动，从黑球运动到点A处开始，用频闪照相机、测速仪测量并记录黑球在木板上的运动时间x（单位：s）、运动速度v（单位：cm/s）、滑行距离y（单位：cm）的数据．

任务一：数据收集

记录的数据如下：

运动时间x/s	0	2	4	6	8	10	…
运动速度v/（cm/s）	10	9	8	7	6	5	…
滑行距离y/cm	0	19	36	51	64	75	…

根据表格中的数值分别在图（b）、图（c）中作出v与x的函数图象、y与x的函数图象：

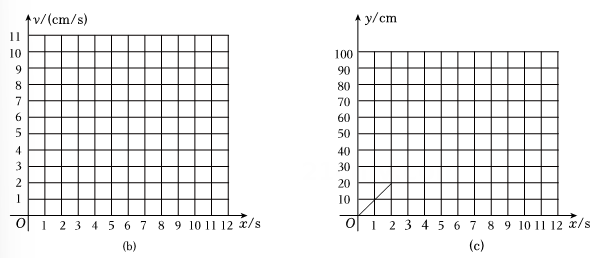(1)、请在图（b）中画出v与x的函数图象：

(2)、【任务二：观察分析】数学兴趣小组通过观察所作的函数图象，并结合已学习过的函数知识，发现图（b）中v与x的函数关系为一次函数关系，图（c）中y与x的函数关系为二次函数关系．请你结合表格数据，分别求出v与x的函数关系式和y与x的函数关系式：（不要求写出自变量的取值范围）

(3)、【任务三：问题解决】当黑球在水平木板停下来时，求此时黑球的滑行距离：

(4)、若黑球到达木板点A处的同时，在点A的前方

n c m

处有一辆电动小车，以2cm/s的速度匀速向右直线运动，若黑球不能撞上小车，则n的取值范围应为．

查看试题解析

专题18 项目式实践——中考数学新考法靶向训练

一、实践探究题