浙江省金华市浦江第五中学2024-2025学年第二学期3月作业检测九年级数学试卷

试卷更新日期：2025-03-12 类型：月考试卷

进入出卷网下载

一、单选题

1. 如果规定收入为正，那么支出为负，收入2元记作＋2元，支出5元记作（　　）

A、5元 B、－5元 C、－3元 D、7元

查看试题解析
2. 如图所示的几何体，其俯视图是（　　）

A、　　　 B、　　 C、　　 D、

查看试题解析
3. 杭州奥体中心体育场里面有80800个座位．数据80800用科学记数法表示为（）

A、 $8.8 \times 1 0^{4}$ B、 $8.08 \times 1 0^{4}$ C、 $8.8 \times 1 0^{5}$ D、 $8.08 \times 1 0^{5}$

查看试题解析
4. 下列运算中正确的是（　　）

A、a＋a²＝a³ B、（2a²）³＝2a⁶ C、a⁶÷a²＝a³ D、a³·a²＝a⁵

查看试题解析
5. 如图，AB是⊙O的直径，点C为⊙O外一点，CA，CD分别与⊙O相切于点A，D，连结BD，AD.若∠ACD＝50°，则∠DBA的度数是（　　）

A、15° B、35° C、65° D、75°

查看试题解析
6. 抛物线的函数表达式为 $y =$ $3 （ x - 2 ）^{2} + 1$ ，若将 $x$ 轴向上平移 2 个单位长度，将 $y$ 轴向左平移 3 个单位长度，则该抛物线在新的平面直角坐标系中的函数表达式为（）

A、 $y = 3 （ x + 1 ）^{2} + 3$ B、 $y = 3 （ x - 5 ）^{2} + 3$ C、 $y = 3 （ x - 5 ）^{2} - 1$ D、 $y = 3 （ x + 1 ）^{2} - 1$

查看试题解析
7. 某景点今年三月接待游客25万人次，五月接待游客60.5万人次．设该景点今年三月到五月接待游客人次的平均月增长率为x（x＞0），则（　　）

A、60.5（1﹣x）²＝25 B、25（1﹣x）²＝60.5 C、60.5（1+x）²＝25 D、25（1+x）²＝60.5

查看试题解析
8. 设二次函数 $y = a (x - m) (x - m - k) (a > 0 ， m ， k$ 是实数 $)$ ，则（）

A、当 $k = 2$ 时，函数 $y$ 的最小值为 $- a$ B、当 $k = 2$ 时，函数 $y$ 的最小值为 $- 2 a$ C、当 $k = 4$ 时，函数 $y$ 的最小值为 $- a$ D、当 $k = 4$ 时，函数 $y$ 的最小值为 $- 2 a$

查看试题解析

二、填空题

9. 分解因式： $4 a^{2} - 1 =$ ．

查看试题解析
10. 如图，点 $D, E$ 分别在 $△ A B C$ 的边 $A B, A C$ 上，且 $D E ∥ B C$ ，点 $F$ 在线段 $B C$ 的延长线上．若 $∠ A D E = 28 °$ ， $∠ A C F = 118 °$ ，则 $∠ A =$ ．

查看试题解析
11. 一个仅装有球的不透明布袋里只有6个红球和 $n$ 个白球（仅有颜色不同）．若从中任意摸出一个球是红球的概率为 $\frac{2}{5}$ ，则 $n =$ ．

查看试题解析
12. 如图，六边形 $A B C D E F$ 是 $⊙ O$ 的内接正六边形，设正六边形 $A B C D E F$ 的面积为 $S_{1}$ ， $△ A C E$ 的面积为 $S_{2}$ ，则 $\frac{S_{1}}{S_{2}} =$ ．

查看试题解析
13. 如图，点 $E$ 在正方形 $A B C D$ 的对角线 $A C$ 上， $E F ⊥ A B$ 于点 $F$ ，连接 $D E$ 并延长，交边 $B C$ 于点 $M$ ，交边 $A B$ 的延长线于点 $G$ ．若 $A F = 4$ ， $F B = 2$ ，则 $M G =$

查看试题解析
14. 图1是一款常见的海绵拖把，图2是其平面示意图，EH是拖把把手，F是把手的一个固定点，海绵安装在两片活动骨架PA，PB上，骨架的端点P只能在线段FH上移动，当海绵完全张开时，PA，PB分别与HM，HN重合；当海绵闭合时，PA，PB与FH重合．已知直杆EH＝120 cm，FH＝20 cm.

(1)、若∠APB＝90°，则EP的长为cm.

(2)、海绵从完全张开到闭合的过程中，直接写出PA的中点Q运动的路径长cm.

查看试题解析

三、解答题

15. （2025－π）⁰+|3－ $\sqrt{12}$ | - 4cos30°+ （ $\frac{1}{2}$ ）^-1

查看试题解析
16. 先化简 $\frac{a^{2} - 4}{a^{2} + 4 a + 4} \div \frac{a - 2}{a^{2} + 2 a} + \frac{a^{2} - a}{a - 1}$ ，再从0，1，2，3中选一个合适的a值代入求值．

查看试题解析
17. 某校为了了解家长和学生观看安全教育视频的情况，随机抽取本校部分学生作调查，把收集的数据按照A ， B ， C ， D四类（A表示仅学生参与；B表示家长和学生一起参与；C表示仅家长参与；D表示其他）进行统计，得到每一类的学生人数，并把统计结果绘制成如图所示的未完成的条形统计图和扇形统计图．

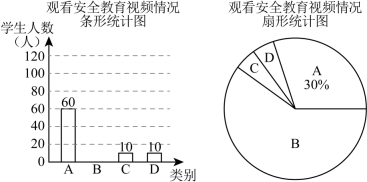(1)、在这次抽样调查中，共调查了多少名学生？

(2)、补全条形统计图．

(3)、在扇形统计图中，求C类学生的扇形的圆心角度数。

(4)、已知该校共有1000名学生，估计B类的学生人数．

查看试题解析
18. 如图，在8×4的网格中，每个小正方形的边长均为1，点A，B，C都是格点（小正方形的顶点），完成下列画图．

(1)、画出△ABC的重心P.

(2)、在已知网格中找出所有格点D，使点△BCD与△ABC的面积相等．

查看试题解析
19. 如图，在正方形ABCD中，点E，F分别在边AB，BC上，∠ADE＝∠CDF.

(1)、求证：AE＝CF.

(2)、连结DB交EF于点O，延长OB至点G，使OG＝OD，连结EG，FG，判断四边形DEGF是不是菱形，并说明理由．

查看试题解析
20. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图，图2是其侧面示意图，其中枪柄BC与手臂MC始终在同一直线上，枪身BA与额头保持垂直．量得胳膊MN＝28 cm，MB＝42 cm，肘关节M与枪身端点A之间的水平宽度为25.3 cm（即MP的长度），枪身BA＝8.5 cm.

(1)、求∠ABC的度数．

(2)、测温时规定枪身端点A与额头距离范围为3～5 cm.在图2中，若测得∠BMN＝68.6°，小红与测温员之间距离为50 cm.问此时枪身端点A与小红额头的距离是否在规定范围内？并说明理由．（结果保留小数点后一位）（参考数据：sin 66.4°≈0.92，cos 66.4°≈0.40，sin 23.6°≈0.40， $\sqrt{2}$ ≈1.414）

查看试题解析
21. 在平面直角坐标系中，设二次函数y=ax²+bx-4a（a，b是常数，a≠0）.

(1)、判断该函数图象与x轴的交点个数，并说明理由。

(2)、若该函数图象的对称轴为直线x=2，A（x₁ ， m），B（x₂ ， m）该函数图象上的任意两点，其中x₁<x₂ ，求当x₁ ， x₂为何值时，m=8a.

(3)、若该函数图象的顶点在第二象限，且过点（1，2），当a<b时，求3a+b的取值范围.

查看试题解析