2025届四川省联合性联考二诊模拟考试数学试题
试卷更新日期:2025-02-21 类型:高考模拟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
-
1. 已知空间中向量=(0,1,0),向量的单位向量为(),则点B到直线AC的距离为( )A、 B、 C、 D、2. 双曲线两个焦点 , 焦距为8,M为曲线上一点,则( )A、1 B、1或9 C、9 D、33. 若函数 , 当时函数值 , 则的取值范围是( )A、 B、 C、 D、4. 存在狄利克雷函数 , 若 , , 则的所有值之和为( )A、3 B、6 C、12 D、135. 已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )A、 B、 C、 D、6. 若方程的四个根组成一个首项为的等差数列,则( )A、1 B、 C、 D、7. 下列说法正确的个数为( )
①180的正因数有16个②以正方体为顶点的三棱锥有70个③+9能被7整除
④投一枚质地均匀的硬币十次,正面朝上频率在 的概率为
A、1个 B、2个 C、3个 D、4个8. 已 知长方形的四个顶点.一质点从的中点沿与夹角为的方向射到上的点后,依次反射到上的点 (入射角等于反射角).设的坐标为.若 , 则的取值范围是( ).A、 B、 C、 D、二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,有选错的得0分.
-
9. 我们知道一元二次方程可以变形为 , 展开后对应项易得到韦达定理,那么类比推理过程,在一个一元三次方程 , 则下列关于此一元三次方程的根的式子正确的是( )A、++=2 B、++= C、= D、++=710. 如图所示,在四个正方体中,是正方体的一条体对角线,点分别为其所在棱的中点,能得出平面的图形为( )A、
 B、
B、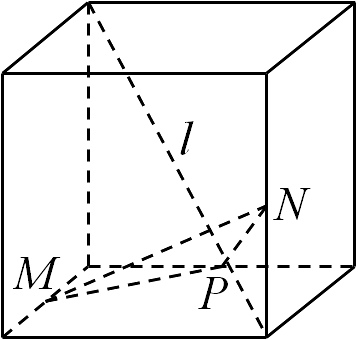 C、
C、 D、
D、 11. 函数 , 向右平移3个单位得到 , 下列说法正确的是( )A、的极小值点为 B、当有两解时, C、若 , , 则 D、若 , 那么 , 且有且仅有一解
11. 函数 , 向右平移3个单位得到 , 下列说法正确的是( )A、的极小值点为 B、当有两解时, C、若 , , 则 D、若 , 那么 , 且有且仅有一解三、填空题:本题共3小题,每小题5分,共15分.
-
12. 展开式中的系数是13. 已知双曲线中心在原点且一个焦点为 , 直线与其相交于 , 两点,中点横坐标为 , 则此双曲线的方程是.14. 已知设P:函数在R上单调递减.Q:不等式的解集为R,如果P和Q有且仅有一个正确,则的取值范围为.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
-
15. 记锐角的内角A、B、C的对边分别为a,b,c,已知.(1)、求的值.(2)、若 , 求边上的高的取值范围.16. 如图,在直三棱柱中,底面是等腰直角三角形, , 侧棱 , D、E分别是与的中点,点E在平面ABD上的射影是的重心.
(Ⅰ)求与平面ABD所成角的余弦值
(Ⅱ)求点到平面的距离
 17. 小杨上的高中食堂有3种套餐,小王第一次选择A,B,C三种套餐的概率相等,若某次选择A之后,下一次仍会在三种套餐以相等概率继续选择,若某次选择B套餐之后,下一次只会在B,C两种套餐中以相等概率去选择,在某次选择C套餐之后,以后只会选择C套餐,根据以上规则回答下列问题:(1)、试写出第n次选择时,小王选A套餐的概率表达式,并求出第3次选择B套餐的概率.(2)、试写出第n次选择时,小王选B套餐的概率表达式,并求出选A套餐的均值.
17. 小杨上的高中食堂有3种套餐,小王第一次选择A,B,C三种套餐的概率相等,若某次选择A之后,下一次仍会在三种套餐以相等概率继续选择,若某次选择B套餐之后,下一次只会在B,C两种套餐中以相等概率去选择,在某次选择C套餐之后,以后只会选择C套餐,根据以上规则回答下列问题:(1)、试写出第n次选择时,小王选A套餐的概率表达式,并求出第3次选择B套餐的概率.(2)、试写出第n次选择时,小王选B套餐的概率表达式,并求出选A套餐的均值.

