浙江省宁波市鄞州中学2023-2024学年高二下学期期中数学试题

试卷更新日期：2024-08-30 类型：期中考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 若集合 $A = \{x ∣ y = \lg (4 - x^{2})\}$ ， $U = R$ ，则下列阴影部分可以表示 $∁_{U} A$ 的为（）

A、 B、 C、 D、

查看试题解析
2. 若a，b是空间中的两条直线，则“a，b异面”是“a，b没有公共点”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 如图，为某组数据的散点图，由最小二乘法计算得到回归直线 $l_{1}$ 的方程为 $\hat{y} = {\hat{b}}_{1} x + {\hat{a}}_{1}$ ，相关系数为 $r_{1}$ ，决定系数为 $R_{1}^{2}$ ．若经过残差分析后去掉点P，剩余的点重新计算得到回归直线 $l_{2}$ 的方程为 $\hat{y} = {\hat{b}}_{2} x + {\hat{a}}_{2}$ ，相关系数为 $r_{2}$ ，决定系数为 $R_{2}^{2}$ ．则下列结论一定正确的是（）

A、 $r_{1} > r_{2}$ B、 $R_{1}^{2} > R_{2}^{2}$ C、 ${\hat{b}}_{1} < {\hat{b}}_{2}$ D、 $r_{1} > 0$ ， $r_{2} < 0$

查看试题解析
4. 若 $2^{27} + a$ 既能被9整除又能被7整除，则正整数a的最小值为（）

A、6 B、10 C、55 D、63

查看试题解析
5. 已知甲、乙两个袋子各装有10个球，其中甲袋子中装有4个黑球、3个白球和3个红球，乙袋子中装有3个黑球、2个白球和5个红球.规定抛掷一枚质地均匀的硬币，若正面朝上，则从甲袋子中随机摸出一个球：若反面朝上，则从乙袋子中随机换出一个球，下列概率中等于 $0.4$ 的为（）

A、摸到黑球 B、摸到红球 C、在抛出的硬币正面朝上的条件下，摸到白球 D、在抛出的硬币反面朝上的条件下，摸到红球

查看试题解析
6. 若函数 $f (x) = 24 a x^{3} + 4 x^{2} - x$ 在区间 $(- 1, 1)$ 恰有两个零点，则实数a的取值范围是（）

A、 $\{- \frac{1}{6}\} \cup (- \frac{1}{8}, \frac{5}{24})$ B、 $\{- \frac{1}{6}\} \cup [- \frac{1}{8}, \frac{5}{24})$ C、 $\{- \frac{1}{6}\} \cup (- \frac{1}{8}, \frac{5}{24}]$ D、 $\{- \frac{1}{6}\} \cup [- \frac{1}{8}, \frac{5}{24}]$

查看试题解析
7. 如图，某种雨伞架前后两排共8个孔，编号分别为 $1 - 8$ 号．若甲、乙、丙、丁四名同学要放伞，每个孔最多放一把伞，则甲放在奇数孔，乙放在偶数孔，且丙、丁没有放在同一排的放法有（）

A、68种 B、136种 C、272种 D、544种

查看试题解析
8. 已知平面向量 $\vec{O A}$ ， $\vec{O B}$ ， $\vec{O C}$ 满足 $|\vec{O A}| = |\vec{O B}| = |\vec{O C}| = \vec{O A} \cdot \vec{O B} = 2$ ，且 $⟨\vec{O A}, \vec{O C}⟩ + ⟨\vec{O B}, \vec{O C}⟩ = \frac{π}{3}$ .若 $x, y \in R$ ，则 $|x \vec{O A} - y \vec{O B}| + |x \vec{O A} - \vec{O C}| + |y \vec{O B} - \vec{O C}|$ 的最小值为（）

A、3 B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析

二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得3分，有选错的得0分.

9. 下列式子恒成立的有（）

A、 $2^{- 0.2} > 2^{- 2}$ B、 $2^{- 0.3} > \ln 0.3$ C、 $\log_{4} 8 > \tan \frac{π}{3}$ D、 $\log_{0.5} 3 = \log_{2} \frac{1}{3}$

查看试题解析
10. 已知函数 $f (x) = 2 \sin (ω x + \frac{π}{6}) \cos (ω x + \frac{π}{6})$ ．若函数 $f (x)$ 图象的两条相邻对称轴的距离为 $\frac{π}{2}$ ，则下列说法正确的有（）

A、函数 $f (x)$ 的最大值为2 B、函数 $f (x)$ 的最小正周期为 $π$ C、函数 $f (x)$ 的图象向右平移 $\frac{π}{3}$ 得到函数 $g (x) = sin 2 x$ 的图象 D、函数 $f (x)$ 的单调递增区间为 $[- \frac{5 π}{12} + k π, \frac{π}{12} + k π] (k \in Z)$

查看试题解析
11. 如图，已知正三棱台 $A B C - A_{1} B_{1} C_{1}$ 的上、下底面边长分别为2和3，侧棱长为1，点P在侧面 $B C C_{1} B_{1}$ 内运动（包含边界）．若直线AP与平面 $B C C_{1} B_{1}$ 所成角的正切值为 $\sqrt{6}$ ，则下列正确的为（）

A、存在点P和点 $Q \in B_{1} C_{1}$ ，使得 $A P / / A_{1} Q$ B、在此三棱台中放置一个球体，其体积最大为 $\frac{\sqrt{6} π}{8}$ C、线段CP长度的取值范围为 $[\sqrt{3} - 1, \sqrt{7}]$ D、所有满足条件的动线段AP形成的曲面面积为 $\frac{\sqrt{7} π}{3}$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分.

12. 已知随机变量X服从二项分布 $X ~ B (8, \frac{1}{2})$ ，且随机变量Y服从正态分布 $N (2, σ^{2})$ ．若 $P (Y \geq E (X)) = 0.2$ ，则 $P (Y \geq 0) =$ ．

查看试题解析
13. 若复数z是关于x的方程 $x^{2} - 2 x + 3 = 0$ 的一个根，则复数z可以是．（写出满足条件的一个即可）

查看试题解析
14. 已知函数 $f (x)$ 的定义域为 $R$ ，且 $f (x + 2)$ 为偶函数， $f (x + 3)$ 为奇函数；当 $x \in [0, 1]$ 时， $f (x) = k \cdot 2^{x} + b (k, b \in R)$ ．若 $f (2024) = 2$ ，则 $\sum_{i = 0}^{2024} (2 i + 1) f (\frac{2 i + 1}{2}) =$ ．

查看试题解析

四、解答题：本题共5小题，其中第15题13分、第16-17题各15分、第18-19题各17分，共77分.解答应写出文字说明、证明过程或演算步骤.

15. 在① $a = b \cos C + \frac{\sqrt{3}}{3} c \sin B$ ， ② $2 b \cos B = c \cos A + a \cos C$ 这两个条件中任选一个补充在下面的横线中，并解答．
已知 $△ A B C$ 中，内角A，B，C所对的边分别为a，b，c，且________．

(1)、求角B的大小；

(2)、若a，b，c成等差数列，判断 $△ A B C$ 的形状并加以证明．

查看试题解析
16. 某城市地铁将于2024年5月开始运营，为此召开了一个价格听证会，拟定价格后又进行了一次调查，随机抽查了50人，他们的收入与态度统计数据如下表：
月收入
（单位：百元）
$[15, 25)$
$[25, 35)$
$[35, 45)$
$[45, 55)$
$[55, 65)$
$[65, 75]$
赞成定价者人数
2
2
4
5
3
4
认为价格偏高者人数
4
8
9
6
2
1

(1)、若以区间的中点值为该区间内的人均月收入，分别求出参与调查的人员中“赞成定价者”与“认为价格偏高者”的月平均收入；

(2)、根据以上统计数据填下面 $2 \times 2$ 列联表，依据小概率值 $α = 0.01$ 的独立性检验，可否认为“月收入以55百元为分界点对地铁定价的态度有差异”？
对地铁定价的态度
人均月收入
合计
不低于55百元的人数
低于55百元的人数
认为价格偏高者
赞成定价者
合计
附： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．
参考数据
$α$
0.1
0.05
0.01
0.005
$x_{α}$
2.706
3.841
6.635
7.879

查看试题解析
17. 如图，多面体 $A B C D E$ 中，直角梯形 $A B C D$ 所在平面与正三角形 $A B E$ 所在平面垂直， $∠ A D C = 90 °$ ， $A B = A D = 2 C D = 4$ ．

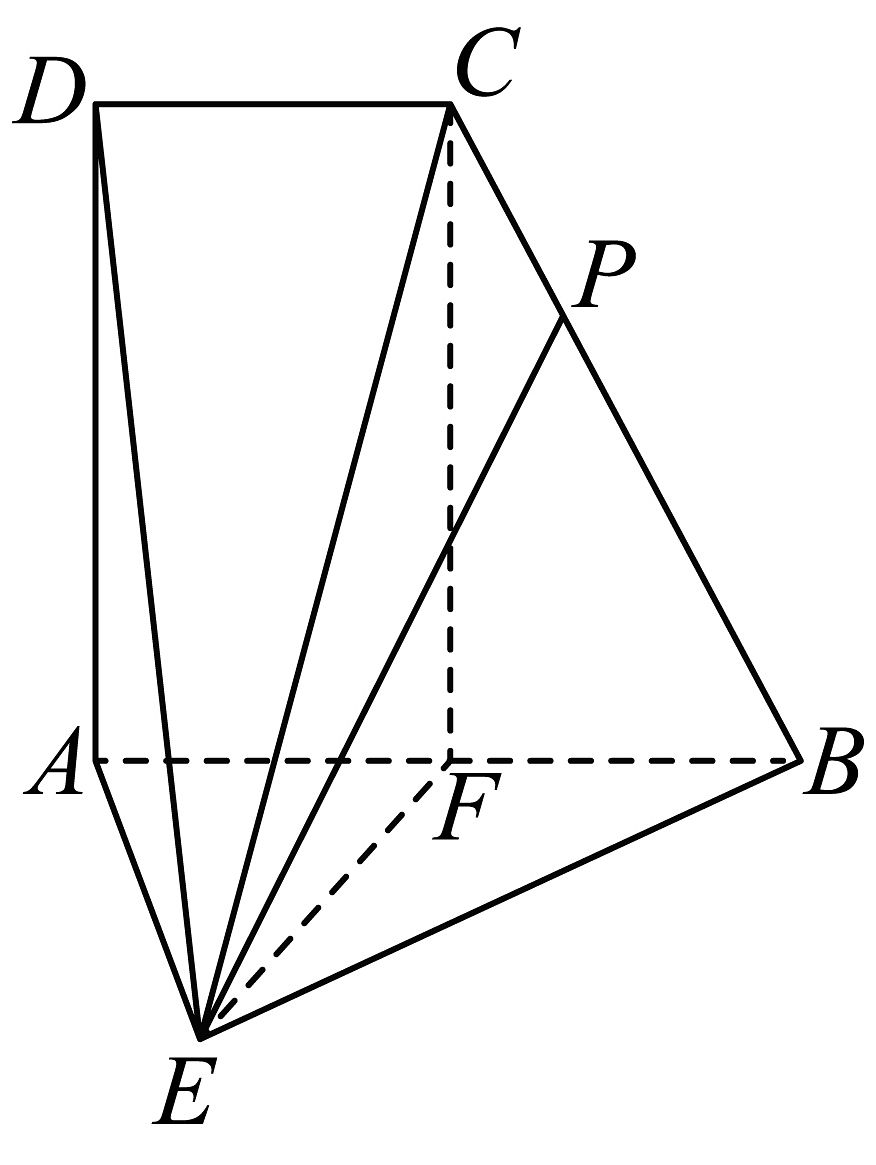(1)、求该多面体的体积V；

(2)、在棱 $B C$ 上是否存在点P，使得直线 $P E$ 和平面 $A D E$ 所成的角大小为 $30 °$ ？若存在，求出 $\frac{B P}{B C}$ 的值；若不存在，请说明理由．

查看试题解析
18. 2023年11月，宁波市余姚河姆渡遗址迎来发掘五十周年，为引导青少年了解河姆渡文化，某校组织全体学生参加河姆渡历史文化知识竞赛，现从中抽取100名学生的成绩组成样本，并将得分分成以下6组： $[40, 50)$ ， $[50, 60)$ ， $[60, 70)$ ， $[70, 80)$ ， $[80, 90)$ ， $[90, 100]$ ，统计结果如图所示．

(1)、试估计这100名学生的众数和中位数（保留一位小数）；

(2)、从样本中得分不低于70分的学生中，用分层抽样的方法选取11人进行座谈，若从座谈名单中随机抽取3人，记得分在 $[90, 100]$ 的人数为X，试求X的分布列和均值：

(3)、以样本估计总体，根据频率分布直方图，可以认为参加知识竞赛的学生得分X近似服从正态分布 $N (μ, σ^{2})$ ，经计算 $σ^{2} = 42.25$ ．若 $μ - σ < X \leq μ + 3 σ$ ，参赛学生可获得“参赛纪念证书”：若 $X > μ + 3 σ$ ，参赛学生可获得“参赛先锋证书”．已知该校共600名学生参加本次文化竞赛活动，试估计获得“参赛纪念证书”的学生人数，并判断竞赛成绩为90分的学生能否获得“参赛先锋证书”．
附：若 $X \sim N (μ, σ^{2})$ ，则 $P (μ - σ < X \leq μ + σ) \approx 0.6827$ ， $P (μ - 2 σ < X \leq μ + 2 σ) \approx 0.9545$ ， $P (μ - 3 σ < X \leq μ + 3 σ) \approx 0.9973$ ；

查看试题解析
19. 已知函数 $y = f (x)$ 的定义域为M，区间 $I \subseteq M$ ，对任意 $x_{1}$ ， $x_{2} \in I$ 且 $x_{1} < x_{2}$ ，记 $Δ x = x_{2} - x_{1}$ ， $Δ y = f (x_{2}) - f (x_{1})$ ．若 $Δ y + Δ x > 0$ ，则称 $f (x)$ 在I上具有性质A；若 $Δ y - Δ x > 0$ ，则称 $f (x)$ 在I上具有性质B：若 $Δ y \cdot Δ x > 0$ ，则称 $f (x)$ 在I上具有性质C；若 $\frac{Δ y}{Δ x} > 0$ ，则称 $f (x)$ 在I上具有性质D．

(1)、记①充分不必要条件：②必要不充分条件；③充要条件；④既不充分也不必要条件，
则 $f (x)$ 在I上单调递增是 $f (x)$ 在I上具有性质A的________（填正确选项的序号）：
$f (x)$ 在I上单调递增是 $f (x)$ 在I上具有性质B的________（填正确选项的序号）；
$f (x)$ 在I上单调递增是 $f (x)$ 在I上具有性质D的________（填正确选项的序号）；

(2)、若 $f (x) = a {(x + 1)}^{2} - 1$ 在 $[1, + \infty)$ 满足性质B，求实数a的取值范围；

(3)、是否存在m， $n \in R$ ，使得函数 $g (x) = \frac{2}{| x - 1 |}$ 在区间 $[m, n]$ 上恰满足性质A，B，C，D中的一个？若不存在，请说明理由：若存在，求实数m的最小值．

查看试题解析

对地铁定价的态度	人均月收入		合计
对地铁定价的态度	不低于55百元的人数	低于55百元的人数	合计
认为价格偏高者
赞成定价者
合计

$α$	0.1	0.05	0.01	0.005
$x_{α}$	2.706	3.841	6.635	7.879