浙江宁波镇海蛟川书院2025年中考数学一模试卷

试卷更新日期：2025-03-05 类型：中考模拟

进入出卷网下载

一、选择题（每小题4分，共40分，在每小题给出的四个选项中，只有一项符合题目要求）

1. 大、中、小三个正方形摆放如图所示，若大正方形的面积为5，小正方形的面积为1，则正方形 $A B C D$ 的边长可能是（）

A、1 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、3

查看试题解析
2. 在网格中，每个小正方形的顶点称为格点．如图，在 $4 \times 4$ 的网格中，点 $A$ 、 $B$ 、 $C$ 都在格点上，那么 $∠ B A C$ 的正切值是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $2$ D、 $\frac{1}{2}$

查看试题解析
3. 有4根细木棒，它们的长度分别是 $3 c m, 5 c m, 7 c m, 9 c m$ .从中任取3根饸好能搭成一个三角形的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
4. 已知关于 $x$ 的分式方程 $\frac{2 x}{x - 1} = \frac{m}{x - 1} + 5$ 有增根，则 $m$ 的值是（）

A、-3 B、-2 C、0 D、2

查看试题解析
5. 如图，圆的周长为4个单位长度，在该圆的4等分点处分别标上0，1，2，3，先让圆周上表示数字0的点与数轴上表示-1的点重合，再将圆沿着数轴向右滚动，则数轴上表示2025的点与圆周上表示哪个数字的点重合？（）

A、0 B、1 C、2 D、3

查看试题解析
6. 已知 $(x - 2021)^{2} + (x - 2025)^{2} = 34$ ，则 $(x - 2023)^{2}$ 的值是（）

A、13 B、11 C、9 D、8

查看试题解析
7. 如图，在平面直角坐标系中，A、B两点在反比例函数 $y = \frac{k}{x} (k > 0, x > 0)$ 的图像上，延长AB交 $x$ 轴于点 $C$ ，且 $A B = B C, D$ 是第二象限一点，且 $D O / / A B$ ，若 $△ A D C$ 的面积是15，则 $k$ 的值为（）

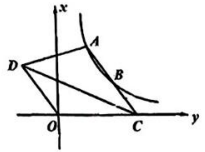A、8 B、10 C、11.5 D、13

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A C B = 9 0^{°}, ∠ A B C = 3 0^{°}, A C = 1$ ，点 $N$ 是BC边上的一点，且 $\frac{B N}{C N} = \frac{2}{1}$ ，点 $M$ 是AC边上一个动点，连接MN ，以MN为直角边，点 $M$ 为直角顶点，在MN的左侧作等腰直角三角形MNQ ，则CQ的最小值是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\sqrt{2}$ D、 $\frac{3}{2}$

查看试题解析
9. 在菱形ABCD中，点E ， F分别是AB ， AD的中点，连接CE ， CF.若 $s i n ∠ E C F = \frac{3}{5}$ ， $C E = 10$ ，则BC的长为（）

A、 $4 \sqrt{5}$ B、 $4 \sqrt{3}$ C、 $3 \sqrt{6}$ D、6

查看试题解析
10. 如图，已知 $△ A B C$ 内接于 $⊙ O$ ，点 $M$ 为BC的中点，连结AM交 $⊙ O$ 于点 $E$ ，且 $C$ 为 $\overset{⌢}{A E}$ 的中点，连结CE ，在BC上存在点 $H$ ，使得 $∠ H E M = \frac{1}{2} ∠ B C A$ ，若 $B H = 2$ ，则AC的长（）

A、4 B、 $4 \sqrt{2}$ C、 $2 + 2 \sqrt{2}$ D、 $4 + \sqrt{2}$

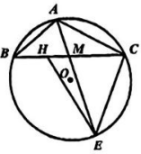查看试题解析

二、填空题（每小题5分，共40分）

11. 在矩形ABCD中， $A B = 5, B C = 10$ ，点 $F$ 在线段AD上，且 $A F = 3$ ，则点 $F$ 到矩形对角线所在直线的距离是.

查看试题解析
12. 若方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解是 ${\begin{array}{l} x = 5 \\ y = 6 \end{array}$ ，则方程组 ${\begin{array}{l} 5 a_{1} x - 3 b_{1} y = 4 c_{1} \\ 5 a_{2} x - 3 b_{2} y = 4 c_{2} \end{array}$ 的解是.

查看试题解析
13. 《九章算术》中有一道关于古代驿站送信的题目，其白话译文为：一份文件，若用慢马送到800里远的城市，所需时间比规定时间多1天；苦改为快马派送，则所需时间比规定时间少2天，已知快马的速度是慢马的 $\frac{4}{3}$ 倍，则规定时间为天.

查看试题解析
14. 小明在研究函数特性时，给出了这样的定义：对于函数图象上的点 $P (x, y)$ ，若 $| x | \leq 1$ 且 $| y | \leq 1$ ，则称点 $P$ 为该函数的“轴近点”.已知一次函数 $y = k x - 3 k$ （ $k$ 为常数）的图象上存在“轴近点”，则 $k$ 的取值范围.

查看试题解析
15. 如图，已知正方形ABCD的边长为3，P是BC中点，点 $F$ 在BD上且满足 $A F ⊥ P F$ ，延长AF分别交CD于点 $M$ ，交BC的延长线于点 $E$ ，则EM的长为.

查看试题解析
16. 如图， $△ O A B$ 为直角三角形，且 $O A ⊥ A B$ ，以 $O$ 为圆心，OA为半径作圆与OB交于点 $E$ ，过点 $A$ 作 $A F ⊥ O E$ 于点 $F$ 交圆 $O$ 于点 $C$ ，延长AO交圆 $O$ 于点 $D$ ，连结DE交AC于点 $M$ ，若圆 $O$ 的半径为 $5, t a n ∠ D = \frac{3}{4}$ ，则AM的长为.

查看试题解析
17. 已知二次函数 $y = a x^{2} + a x - 4$ ，其顶点纵坐标为 $- \frac{9}{2}$ ，点 $Q (k, h)$ 在该函数图象上，若在点 $Q$ 右侧（不含点）的函数图象上，恰好有三个点到 $x$ 轴的距离为 $\frac{7}{2}$ ，则 $k$ 的取值范围是.

查看试题解析
18. 如图所示，在 $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ，点 $D$ 为AC上一点，满足 $\frac{C D}{B C} = \frac{3}{4}$ ，且 $\frac{A D}{C D} = n$ ，过点 $C$ 作 $C P ⊥ B D$ 于 $P$ 点，连接AP交CB于点 $Q$ ，则 $t a n ∠ C P Q =$ （结果用含 $n$ 的代数式表达）

查看试题解析

三、解答题（本大题有6小题，共70分）

19. 在不透明的袋中有大小、形状和质地等完全相同的小球，它们分别标有数字 $- 2 、 - 1 、 3$ .从袋中任意摸出一个小球，然后放回，将袋中的小球搅匀后，再从袋中摸出另一小球.

(1)、请你用列表或画树状图的方法表示摸出小球上的数字可能出现的所有结果.

(2)、将第一次摸出的数字作为点的横坐标 $x$ ，第二次摸出的数字作为点的纵坐标 $y$ ，求点落在双曲线上 $y = \frac{2}{x}$ 的概率.

查看试题解析
20. 如图，在 $4 \times 4$ 的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫做格点， $△ A B C$ 的顶点均在格点上.

(1)、在 $△ A B C$ 的边AB上找到一点 $D$ ，连结CD ，使得 $△ A C D$ 的面积与 $△ B C D$ 的面积之比为3：2，请仅用无刻度的直尺在给定网格中完成画图，并保留作图迹.

(2)、在网格中找到一个格点 $E$ （ $E$ 点不同于A、B、C），连结AE、BE ，使得 $∠ A E B = 2 ∠$ ACB ，请仅用无刻度的直尺在给定网格中完成画图，并保留作图痕迹.

查看试题解析
21. 已知点 $M (x_{1}, y_{1}), N (x_{2}, y_{2})$ 在二次函数 $y = a (x - 3)^{2} + 2 (a < 0)$ 的图象上，且满足 $x_{2} - x_{1} = 5$ .

(1)、如图，若二次函数的图象经过点 $(1, 0)$ ，若 $y_{1} = y_{2}$ ，此时二次函数图象的顶点为点 $P$ ，求 $S_{△ R M N}$ ；

(2)、当 $x_{1} ⩽ x ⩽ x_{2}$ 时，二次函数的最大值与最小值的差为1，点M ， N在对称轴的异侧，求 $a$ 的取值范围.

查看试题解析
22. 在平面直角坐标系中，直线 $y = - 2 x + 4$ 文 $x$ 轴于点 $A$ ，交 $y$ 轴于点 $B$ ，点 $C$ 的坐标为 $(1, 0)$ .

(1)、求直线BC的函数表达式.

(2)、点 $D$ 是 $x$ 轴上一动点，连接BD、CD ，当 $△ B C D$ 的面积是 $△ A O B$ 面积的 $\frac{3}{2}$ 时，求点 $D$ 的坐标.

(3)、点 $E$ 坐标为 $(0, - 2)$ ，连接CE ，点 $P$ 为直线AB上一点，若 $∠ C E P = 4 5^{°}$ ，求点 $P$ 坐标.

查看试题解析
23. 如图，已知AB是 $⊙ O$ 的直径， $C$ 是 $⊙ O$ 上一点，CD是 $⊙ O$ 的切线，且 $A D ⊥$ CD于点D ，延长DA交 $⊙ O$ 于点 $M$ ，连结CM交AB于点 $F$ ，

(1)、如图1，作 $C E ⊥ A B$ 于点 $E$ ，
①求证 $△ C D A$ $≅ △ C E A$
②若 $A E = E F, C F = 3$ ，则FM的长.

(2)、若 $\frac{C F}{F M} = \frac{13}{10}$ ，求 $t a n ∠ A M C$ .

查看试题解析
24.

(1)、如图1，在 $△ A B C$ 中， $D$ 是BC上一点， $E F / / B C$ 交AD于点 $G$ ，则 $\frac{E G}{G F} =$ （用图中已有线段表示）；

(2)、如图2，在 $△ A B C$ 中，M、N是AB上的两点，且满足 $B N = N M = M A$ ，在BC上取一点 $D$ ，过点 $D$ 作 $D P / / A C$ 分别交CM的延长线、CN于点P、Q ，求 $\frac{Q D}{Q P}$ 的值；

(3)、如图3，在正方形ABCD中，点 $E$ 是BC上一点，连结AE交BD于点 $F$ ，在AF上取一点 $P$ ，使得 $∠ B P D = 13 5^{°}$ ，若 $\frac{P D}{P B} = \frac{\sqrt{10}}{2}, A D = 5$ ，求BE的长.

查看试题解析