浙江省舟山市定海区金衢山五校联考2025年初中数学毕业生第一次质量监测模拟试卷
试卷更新日期:2025-03-05 类型:中考模拟
一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
-
1. 下列两个数中,互为相反数的是( )A、和 B、和 C、和 D、和2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列说法正确的是( )A、为了解我国中学生课外阅读的情况,应采用全面调查的方式 B、一组数据1,2,5,5,5,3,3的中位数和众数都是5 C、抛掷一枚硬币200次,一定有100次"正面朝上” D、若甲组数据的方差是0.03,乙组数据的方差是0.1,则甲组数据比乙组数据稳定4. 小莉用几个体积是1立方厘米的正方体摆成了一个几何体.如图是从不同方向看到的图形.这个几何体的体积是( )立方厘米.
3. 下列说法正确的是( )A、为了解我国中学生课外阅读的情况,应采用全面调查的方式 B、一组数据1,2,5,5,5,3,3的中位数和众数都是5 C、抛掷一枚硬币200次,一定有100次"正面朝上” D、若甲组数据的方差是0.03,乙组数据的方差是0.1,则甲组数据比乙组数据稳定4. 小莉用几个体积是1立方厘米的正方体摆成了一个几何体.如图是从不同方向看到的图形.这个几何体的体积是( )立方厘米. A、4 B、5 C、6 D、75. 海平面上,有一个灯塔,测得海岛A在灯塔北偏东30°方向上,同时测得海岛B在灯塔北偏东60°的方向上,则灯塔的位置可以是( )
A、4 B、5 C、6 D、75. 海平面上,有一个灯塔,测得海岛A在灯塔北偏东30°方向上,同时测得海岛B在灯塔北偏东60°的方向上,则灯塔的位置可以是( ) A、点O1 B、点O2 C、点O3 D、点O46. 下列各式在实数范围内不能分解因式的是( )A、 B、 C、 D、7. 在长为18m,宽为15m的长方形空地上,沿平行于长方形各边的方向分别割出三个大小完全一样的小长方形花圃,其示意图如图所示,则其中一个小长方形花圃的面积为( )
A、点O1 B、点O2 C、点O3 D、点O46. 下列各式在实数范围内不能分解因式的是( )A、 B、 C、 D、7. 在长为18m,宽为15m的长方形空地上,沿平行于长方形各边的方向分别割出三个大小完全一样的小长方形花圃,其示意图如图所示,则其中一个小长方形花圃的面积为( ) A、 B、 C、 D、8. 如图,在等腰直角三角形中, . 在边 , 上分别取点D和点E,使 , , 则线段的长为( )
A、 B、 C、 D、8. 如图,在等腰直角三角形中, . 在边 , 上分别取点D和点E,使 , , 则线段的长为( ) A、 B、 C、 D、9. 如图,已知中, , 点为边上任一点,以为圆心,为半径的与交于点 , 连接并延长交于点 , 连接 , 若 , 当最大时,若的半径为 , 则的值为( )
A、 B、 C、 D、9. 如图,已知中, , 点为边上任一点,以为圆心,为半径的与交于点 , 连接并延长交于点 , 连接 , 若 , 当最大时,若的半径为 , 则的值为( ) A、 B、 C、 D、10. 已知反比例函数 的图象与一次函数的图象交于点 , . 则下列各式的值最大的是( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知反比例函数 的图象与一次函数的图象交于点 , . 则下列各式的值最大的是( )A、 B、 C、 D、二、填空题(本题有6小题,每题4分,共24分)
-
11. 用提公因式法分解因式 时,提取的公因式是12. 如图是一个正方形及其内切圆,随机地往正方形内投一粒米,落在圆内的概率为 .
 13. 圆湖周围每隔米栽棵树,共栽了棵,圆湖的周长是 .14. 实数 , 是一元二次方程的两个根,则多项式的值为 .15. 如图所示,已知直线与x、y轴交于B、C两点, , 在内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个 , 第2个 , 第3个 , …则第n个等边三角形的边长等于 .
13. 圆湖周围每隔米栽棵树,共栽了棵,圆湖的周长是 .14. 实数 , 是一元二次方程的两个根,则多项式的值为 .15. 如图所示,已知直线与x、y轴交于B、C两点, , 在内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个 , 第2个 , 第3个 , …则第n个等边三角形的边长等于 . 16. 如图,抛物线的顶点为A,与y轴交于点B,则直线AB的表达式为 .
16. 如图,抛物线的顶点为A,与y轴交于点B,则直线AB的表达式为 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17.(1)、计算:(﹣2)0+- .(2)、请你先化简( -) , 再从0,﹣2,2,1中选择一个合适的数代入,求出这个代数式的值.18. 阅读下面材料,然后解答问题:
解方程: .
分析:本题实际上一元四次方程.若展开按常规解答对于同学们来说还是有一定的挑战性.解高次方程的基本方法是“降次”,我们可以把视为一个整体设为另外一个未知数,可以把原方程降次为一元二次方程来继续解答.我们把这种换元解方程的方法叫做换元法.
解:设 , 则原方程换元为 .
, 解得: ,
或 .
解得 , , , .
请参考例题解法,解下列方程:
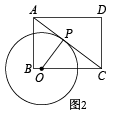
(1)、;(2)、 .19. 如图1,已知矩形中, , , 点P是对角线的中点,点O为射线上的一个动点,连接 , 以为半径作 .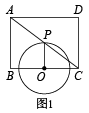
 (1)、如图2,当与相切时,求的半径长;(2)、当点O运动到何处,的半径最小?(3)、在点O的运动过程中,与的三条边有四个交点,求的取值范围.20. 丰富的社会实践活动不仅能让同学们理解生活服务社会,更能帮助同学们树立正确的劳动态度与价值观.为迎接“五一劳动节”,学校将开展以下四项实践活动:A . 博物馆小小解说员,B . 汽车南站送祝福,C . 地铁小义工,D . 警营岗位体验,并让同学们自主选择其中一项参加.以下是从全校学生中随机抽取部分学生进行调查的相关统计图(缺少部分信息).
(1)、如图2,当与相切时,求的半径长;(2)、当点O运动到何处,的半径最小?(3)、在点O的运动过程中,与的三条边有四个交点,求的取值范围.20. 丰富的社会实践活动不仅能让同学们理解生活服务社会,更能帮助同学们树立正确的劳动态度与价值观.为迎接“五一劳动节”,学校将开展以下四项实践活动:A . 博物馆小小解说员,B . 汽车南站送祝福,C . 地铁小义工,D . 警营岗位体验,并让同学们自主选择其中一项参加.以下是从全校学生中随机抽取部分学生进行调查的相关统计图(缺少部分信息).
由图中给出的信息解答下列问题:
(1)、求抽取的学生中选择参加“汽车南站送祝福”活动的人数,并补全条形统计图.(2)、求扇形统计图中“地铁小义工”活动所对应的扇形圆心角的度数.(3)、若该校共有2000名学生,请根据抽样调查的结果,估计该校选择参加“博物馆小小解说员”活动的学生约有多少人?21. 有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度. (1)、如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;(2)、爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到1cm).
(1)、如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;(2)、爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到1cm).(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
22. (1)、【情境再现】
(1)、【情境再现】如图 , 在正方形中,点、分别在边、上,且 , 求证: .
(2)、【迁移应用】如图 , 在矩形中,为常数 , 点、、、分别在矩形的边上,且 , 求证: .
(3)、【拓展延伸】如图 , 在四边形中, , , , 点、分别在边、上,且 ,
 , 求的长.23. 已知平面直角坐标系中,O为坐标原点,抛物线yx2+bx+c与x轴交于A , B两点,与y轴的正半轴交于C点,且B(4,0),BC=4 .
, 求的长.23. 已知平面直角坐标系中,O为坐标原点,抛物线yx2+bx+c与x轴交于A , B两点,与y轴的正半轴交于C点,且B(4,0),BC=4 . (1)、求抛物线的解析式;(2)、如图1,点P是抛物线在第一象限内的一点,连接PB , PC , 过点P作PD⊥x轴于点D , 交BC于点K . 记△PBC , △BDK的面积分别为S1 , S2 , 求S1﹣S2的最大值;(3)、如图2,连接AC , 点E为线段AC的中点,过点E作EF⊥AC交x轴于点F . 抛物线上是否存在点Q , 使∠QFE=2∠OCA?若存在,求出点Q的坐标;若不存在,说明理由.24. 如图,点是矩形中边上一点,沿折叠为 , 点落在上.
(1)、求抛物线的解析式;(2)、如图1,点P是抛物线在第一象限内的一点,连接PB , PC , 过点P作PD⊥x轴于点D , 交BC于点K . 记△PBC , △BDK的面积分别为S1 , S2 , 求S1﹣S2的最大值;(3)、如图2,连接AC , 点E为线段AC的中点,过点E作EF⊥AC交x轴于点F . 抛物线上是否存在点Q , 使∠QFE=2∠OCA?若存在,求出点Q的坐标;若不存在,说明理由.24. 如图,点是矩形中边上一点,沿折叠为 , 点落在上. (1)、求证:;(2)、若 , , 求的值;(3)、在(2)的条件下,在中,动点从点出发,在边上以每秒的速度向点匀速运动,同时动点从点出发,在边上以每秒的速度向点匀速运动,当其中一个点到达终点时另一个点也停止运动,设运动时间为秒,连接 , 若与以点 , , 为顶点的三角形相似,求的值.
(1)、求证:;(2)、若 , , 求的值;(3)、在(2)的条件下,在中,动点从点出发,在边上以每秒的速度向点匀速运动,同时动点从点出发,在边上以每秒的速度向点匀速运动,当其中一个点到达终点时另一个点也停止运动,设运动时间为秒,连接 , 若与以点 , , 为顶点的三角形相似,求的值.