浙江省宁波市南三县(奉化区、宁海县、象山县)2025年九年级下学期中考一模模拟数学试题
试卷更新日期:2025-03-05 类型:中考模拟
一、选择题(每题3分,共30分,每小题给出的四个选项中只有一个选项符合题目要求)
-
1. 下列说法正确的是 ( )A、任何数都不等于它的相反数 B、互为相反数的两个数的同一正偶数次幂相等 C、只有1的倒数是它本身 D、如果大于 , 那么的倒数大于的倒数2. 下列计算正确的是( )A、 B、 C、 D、3. 2024年8月8日至11日期间,椒江葭沚老街举办了台州暑期消费季活动,四天的客流量超过58万人次,现场销售额高达4580000元,其中数据“4580000”用科学记数法表示为( )A、 B、 C、 D、4. 如图是由5个相同的正方体搭成的几何体,这个几何体的左视图是( )
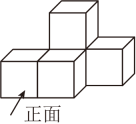 A、
A、 B、
B、 C、
C、 D、
D、 5. 某校举行了科学素质知识竞赛,进入决赛的学生共有名,他们的决赛成绩如表所示:
5. 某校举行了科学素质知识竞赛,进入决赛的学生共有名,他们的决赛成绩如表所示:决赛成绩/分
人数/名
则这10名学生决赛成绩的中位数和众数分别是( )
A、 , B、 , C、 , D、 ,6. 如果点在平面直角坐标系的第三象限内,那么的取值范围在数轴上可表示为( )A、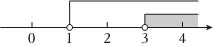 B、
B、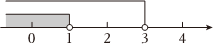 C、
C、 D、
D、 7. 我国古代数学著作《孙子算经》中记载“鸡兔同笼”问题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?若设兔子有x只,鸡有y只,则下列方程组中正确的是( )A、 B、 C、 D、8. 如图,在正方形中,点在边上,是边上的中点,平分 . 若 , 则的长为( )
7. 我国古代数学著作《孙子算经》中记载“鸡兔同笼”问题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?若设兔子有x只,鸡有y只,则下列方程组中正确的是( )A、 B、 C、 D、8. 如图,在正方形中,点在边上,是边上的中点,平分 . 若 , 则的长为( ) A、 B、 C、 D、9. 若关于的一元二次方程有实数根,则字母的取值范围是( )A、且 B、 C、 D、且10. 如图 29-9, 在边长为 1 的小正方形组成的网格中, 四个点均在格点上, 与 相交于点 , 连结 , 则 与 的周长比为 ( )
A、 B、 C、 D、9. 若关于的一元二次方程有实数根,则字母的取值范围是( )A、且 B、 C、 D、且10. 如图 29-9, 在边长为 1 的小正方形组成的网格中, 四个点均在格点上, 与 相交于点 , 连结 , 则 与 的周长比为 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 因式分解:x2y+2xy= .12. 二次根式中字母的取值范围是 .13. 一个不透明的口袋中有3个质地相同的小球,其中2个红色,1个蓝色.随机摸取一个小球是红色小球的概率是 .14. 如图是一个几何体的三视图,则该几何体的侧面积是 .
 15. 如图,长方形ABCD沿AE折叠,使点D落在BC边上的点F处.如果∠BAF=55°,那么∠DAE= , ∠AEF= , ∠EFC=.
15. 如图,长方形ABCD沿AE折叠,使点D落在BC边上的点F处.如果∠BAF=55°,那么∠DAE= , ∠AEF= , ∠EFC=. 16. 如图,在正方形ABCD中,点E是边BC上的动点(不与点B、C重合),∠BAE=∠GEF,AE=EF,FG⊥BC交BC延长线于点G,FQ⊥CD于点Q,连结AF交CD于点H,点P是AF的中点,连结BP.求:
16. 如图,在正方形ABCD中,点E是边BC上的动点(不与点B、C重合),∠BAE=∠GEF,AE=EF,FG⊥BC交BC延长线于点G,FQ⊥CD于点Q,连结AF交CD于点H,点P是AF的中点,连结BP.求: (1)、的度数为(2)、当时,.(用的代数式表示)
(1)、的度数为(2)、当时,.(用的代数式表示)三、解答题(共66分)
-
17. 计算:(1)、(2)、18. 如图, 在 Rt 中, 。
 (1)、尺规作图:作 AB 的垂直平分线 ,交 BC 于点 D ,交 AB 于点 E (不写作法,保留作图痕迹);(2)、 在(1)题图中, 连接 AD , 若 平分 , 且 , 求 的长。19. 今年郑州市受疫情影响,中小学生在家进行线上学习.为了了解学生在家主动锻炼身体的情况,某校随机抽查了部分学生,对他们每天的运动时间进行调查,并将调查统计的结果分为四类:每天运动时间t≤30分钟的学生记为A类,30分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类.收集的数据绘制如下两幅不完整的统计图,
(1)、尺规作图:作 AB 的垂直平分线 ,交 BC 于点 D ,交 AB 于点 E (不写作法,保留作图痕迹);(2)、 在(1)题图中, 连接 AD , 若 平分 , 且 , 求 的长。19. 今年郑州市受疫情影响,中小学生在家进行线上学习.为了了解学生在家主动锻炼身体的情况,某校随机抽查了部分学生,对他们每天的运动时间进行调查,并将调查统计的结果分为四类:每天运动时间t≤30分钟的学生记为A类,30分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类.收集的数据绘制如下两幅不完整的统计图,
请根据图中提供的信息,解答下列问题:
(1)、这次共抽取了名学生进行调查统计;(2)、扇形统计图中D类所对应的扇形圆心角大小为;(3)、将条形统计图补充完整;(4)、学校要求在家主动锻炼身体的时间超过30分钟才达标,若该校共有2000名学生,请你估计该校达标的学生约有多少人?20. 图1是某地下商业街的入口的玻璃顶,它是由立柱、斜杆、支撑杆组成的支架撑起的,图2是它的示意图.经过测量,支架的立柱与地面垂直 , 米,点在同一水平线上,斜杆与水平线的夹角 , 支撑杆 , 垂足为 , 该支架的边与的夹角 , 又测得米. (1)、求该支架的边的长;(2)、求支架的边的顶端到地面的距离.(结果精确到0.1米)(参考数据:)21. 某市半程马拉松比赛,甲乙两位选手的行程千米随时间小时变化的图象如图所示.
(1)、求该支架的边的长;(2)、求支架的边的顶端到地面的距离.(结果精确到0.1米)(参考数据:)21. 某市半程马拉松比赛,甲乙两位选手的行程千米随时间小时变化的图象如图所示. (1)、哪位选手先到终点? 填“甲”或“乙”;
(1)、哪位选手先到终点? 填“甲”或“乙”;
(2)、甲选手跑到千米时,用了 小时起跑 小时后,甲乙两人相遇;
(3)、乙选手在的时段内,与之间的函数关系式是 ;
(4)、甲选手经过小时后,距离起点有 千米.22. 如图,在中, . (1)、求证: .(2)、求证: .23. 小江自制了一把水枪(图1),他将水枪固定,在喷水头距离地面1米的位置进行实验.当喷射出的水流与喷水头的水平距离为2米时,水流达到最大高度3米,该水枪喷射出的水流可以近似地看成抛物线,图2为该水枪喷射水流的平面示意图.
(1)、求证: .(2)、求证: .23. 小江自制了一把水枪(图1),他将水枪固定,在喷水头距离地面1米的位置进行实验.当喷射出的水流与喷水头的水平距离为2米时,水流达到最大高度3米,该水枪喷射出的水流可以近似地看成抛物线,图2为该水枪喷射水流的平面示意图. (1)、求该抛物线的表达式.(2)、在距离喷射头水平距离3米的位置放置一高度为2米的障碍物,试问水流能越过该障碍物吗?(3)、小江通过重新调整喷头处的零件,使水枪喷射出的水流抛物线满足表达式 . 当时,y的值总大于2,请直接写出a的取值范围.24. 已知内接于 , 为的内心,延长交于点 , 交于点 . 连结 , , .
(1)、求该抛物线的表达式.(2)、在距离喷射头水平距离3米的位置放置一高度为2米的障碍物,试问水流能越过该障碍物吗?(3)、小江通过重新调整喷头处的零件,使水枪喷射出的水流抛物线满足表达式 . 当时,y的值总大于2,请直接写出a的取值范围.24. 已知内接于 , 为的内心,延长交于点 , 交于点 . 连结 , , . (1)、若求的度数;(2)、设四边形的面积记为 , 连结 , 当时,请完成下列问题.
(1)、若求的度数;(2)、设四边形的面积记为 , 连结 , 当时,请完成下列问题.①求证∶
②已知求的值.