浙江省绍兴市2025年中考一模数学模拟试题

试卷更新日期：2025-03-05 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）

1. 若 $|a - 1| = 1$ ， $b = - 3$ ，则 $a - b =$ （）

A、 $- 4$ 或 $- 2$ B、 $4$ 或 $2$ C、 $- 1$ 或 $5$ D、 $5$ 或 $3$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{8} \div a^{4} = a^{2}$ C、 ${(a^{3})}^{4} = a^{7}$ D、 ${(2 a)}^{3} = 8 a^{3}$

查看试题解析
3. 下列说法：①一个数的绝对值一定是正数；②一个角的补角一定比这个角大；③若 $A P = B P$ ，则P是线段 $A B$ 的中点；④多项式 $x^{3} + x^{2} - 5 x + 1$ 是三次四项式；⑤同角的余角相等．其中正确的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 下列语句中：
①经过一点有且只有一条直线与已知直线垂直；②过一点有且只有一条直线与已知直线平行；③互为邻补角的两个角的平分线互相垂直；④有公共顶点且相等的角是对顶角，其中错误的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 假期到了， 17 名女教师去外地培训，住宿时有 2 人间和 3 人间可供租住，每个房间都要住满，她们的租住方案有（）

A、5 种
B、4 种
C、3 种
D、2 种

查看试题解析
6. 如图，电路图上有1个小灯泡以及4个断开状态的开关A，B，C，D，现随机闭合两个开关，小灯泡发光的概率为（　）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{1}{2}$

查看试题解析
7. 某商店一月份的利润为 $50$ 万元，二、三月份的利润平均增长率为 $m$ ，则下列各式中，能正确表示这个商店第一季度的总利润的是（）

A、 $50 （ 1 + m ）$ 万元 B、 $50 {(1 + m)}^{2}$ 万元 C、 $[50 + 50 (1 + m)]$ 万元 D、 $[50 + 50 (1 + m) + 50 {(1 + m)}^{2}]$ 万元

查看试题解析
8. 如图，分别以点A，B为圆心，大于 $\frac{1}{2}$ AB 的长为半径作弧，交点分别为 M，N，连结MN交AC 于点D，下列说法一定正确的是（）

A、△ABD是直角三角形 B、△BCD是等腰三角形 C、△ABD是等腰三角形 D、△ABC是等腰三角形

查看试题解析
9. 如图， $A B ∥ C D$ ， F为 $A B$ 上一点， $F D ∥ E H$ ，且 $F E$ 平分 $∠ A F G$ ，过点F作 $F G ⊥ E H$ 于点G，且 $∠ A F G = 2 ∠ D$ ，则下列结论：① $∠ D = 30 °$ ；② $2 ∠ D + ∠ E H C = 90 °$ ；③ $F D$ 平分 $∠ H F B$ ；④ $F H$ 平分 $∠ G F D$ ．其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，正方形 $A B C D$ ，分别取 $A D$ 和 $C D$ 边的中点 $E$ 、 $F$ ，连接 $B E$ 、连接 $A F$ 相交于点 $G$ ，连接 $C G$ ，若 $∠ A B E = α$ ，则 $∠ D C G$ 的度数为（）

A、 $45 ° - \frac{1}{2} a$ B、 $45 ° + \frac{1}{2} α$ C、 $90 ° - α$ D、 $90 ° - 2 α$

查看试题解析

二、填空题（本大题共6小题，每小题5分，共30分）

11. 为备战东营市第十二届运动会，某县区对甲、乙、丙、丁四名射击运动员进行射击测试，他们射击测试成绩的平均数 $\bar{x}$ （单位：环）及方差 $S^{2}$ （单位：环²）如下表所示：

甲
乙
丙
丁

$\bar{x}$

$9.6$

$8.9$

$9.6$

$9.6$

$S^{2}$

$1.4$

$0.8$

$2.3$

$0.8$
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择．

查看试题解析
12. 如图， $△ A B C$ 中， $A B = A C = 6$ ， $∠ B A C = 60 °$ ，延长 $A B$ 至点E，连接 $C E$ ，若 $△ A E C$ 的周长为 $25$ ，则 $△ B C E$ 的周长为

查看试题解析
13. 如图，图1是由6块完全相同的三角形地砖铺成，图2是由10块完全相同的三角形地砖铺成，图3是由14块完全相同的三角形地砖铺成，…，按图中所示规律，图n所需三角形地砖数量为482块，则n的值为．

查看试题解析
14. 如图，在平面直角坐标系中，将抛物线 $C_{1}$ ： $y = x^{2}$ 绕原点 $O$ 顺时针旋转 $180 °$ 后得到 $C_{2}$ ，向右平移4个单位，向上平移2个单位得到 $C_{3}$ ．点 $A$ 为 $C_{3}$ 的顶点，作直线 $O A$ ．点 $Q (0, m)$ 为平面内一动点，将点 $Q$ 向上平移两个单位长度得到点 $B$ ，过点 $B$ 作y轴的垂线交直线 $O A$ 于点 $C$ ，以 $B C$ 、 $B Q$ 为边构造矩形 $B Q D C$ ．设 $C_{1}$ 、 $C_{2}$ 、 $C_{3}$ 的图象为 $G$ ．当矩形 $B Q D C$ 与图象 $G$ 有三个公共点时， $m$ 的取值范围为．

查看试题解析
15. 在 $R t △ A B D$ 中， $∠ A B D = 90 °$ ，点 $C$ 在线段 $A D$ 上，过点 $C$ 作 $C E ⊥ A B$ 于点 $E$ ， $C F ⊥ B D$ 于点 $F$ ，使得四边形 $C E B F$ 为正方形，此时 $A C = 3 cm$ ， $C D = 4 cm$ ，则阴影部分面积为 ${cm}^{2}$ ．

查看试题解析
16. 平面直角坐标系中有点 $A (0, 6)$ 、 $b (8, 0)$ ，连接 $A B$ ，以 $A B$ 为直角边在第一象限内作等腰直角三角形 $A B C$ ，则点C的坐标是.

查看试题解析

三、解答题（本大题有8小题，第17～20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程）

17. 先化简，再求值： $\frac{2}{x^{2} - 4} \div (1 - \frac{x}{x + 2})$ ，其中 $x = \sqrt{3} + 2$ ．

查看试题解析
18. 如图， $A B$ 是 $⊙ O$ 的直径，延长弦 $B D$ 到点 $C$ ，使 $D C = B D$ ，连接 $A C$ ，过点 $D$ 作 $D E ⊥ A C$ ，垂足为 $E$ ．

(1)、判断直线 $D E$ 与 $⊙ O$ 的位置关系，并证明你的结论；

(2)、若 $⊙ O$ 的半径为6， $∠ B A C = 60 °$ ，延长 $E D$ 交 $A B$ 延长线于点 $F$ ，求阴影部分的面积．

查看试题解析
19. 综合与实践活动中，某数学兴趣小组利用所学的知识测量矩形广告牌的高度．
如图，在地面 $A$ 处测得广告牌顶端顶点 $C$ 的仰角为 $45 °$ ，走向广告牌 $6 m$ 到达 $B$ 处，在 $B$ 处测得广告牌低端顶点 $D$ 的仰角为 $66 °$ ，已知 $C D = 2 m$ ，立柱 $G H$ 垂直于 $A B$ ，且点 $A$ ， $B$ ， $H$ 在同一条水平直线上．（矩形广告牌与立柱 $G H$ 垂直）过点 $D$ 作 $D E ⊥ A B$ ，垂足为 $E$ ．设 $D E = h$ （单位： $m$ ）．

(1)、用含有 $h$ 和 $\tan 66 °$ 的式子表示线段 $B E$ 的长；

(2)、求广告牌低端顶点 $D$ 到地面的距离 $D E$ 的长．（ $\tan 66 °$ 取 $2.25$ ，结果取整数）

查看试题解析
20. 已知甲、乙两地相距90km，A，B两人沿同一公路从甲地出发到乙地，A骑摩托车，B骑电动车，图中DE，OC分别表示A，B离开甲地的路程 $s (km)$ 与时间 $t (h)$ 的函数关系的图象，根据图象解答下列问题．

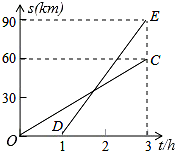(1)、A比B后出发几个小时？B的速度是多少？

(2)、在B出发后几小时，两人相遇？

查看试题解析
21. 一个不透明的口袋中装有若干个红球、 1 个白球、 1 个黑球，这些球除颜色外都相同，将球摇匀.

(1)、从中任意摸出 1 个球，恰好摸到红球的概率是 $\frac{1}{2}$ ，则红球有 ▲ 个；

(2)、在（1）的条件下，从袋中任意摸出 2 个球，请用画树状图或列表的方法求摸出的球是一个红球和一个白球的概率.

查看试题解析
22. 已知：如图， $E$ 是正方形 $A B C D$ 对角线 $B D$ 上的一点，且 $B E = B C ， E F ⊥ B D$ ，垂足为 $E$ ，交 $D C$ 于点 $F$ ．
求证： $D E = C F$ ．

查看试题解析
23. 已知：如图， $∠ A B D = ∠ A C D = 90 °, ∠ 1 = ∠ 2$ ．求证： $A D$ 平分 $∠ B A C$ ．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与y轴交于点 $C (0, 3)$ ，与x轴交于A、B两点，点B坐标为 $(4, 0)$ ，抛物线的对称轴方程为 $x = 1$ ．

(1)、求抛物线的解析式；

(2)、点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设 $△ M B N$ 的面积为S ，点M运动时间为t ，试求S与t的函数关系，并求S的最大值；

(3)、在点M运动过程中，是否存在某一时刻t ，使 $△ M B N$ 为直角三角形？若存在，求出t值；若不存在，请说明理由．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	$9.6$	$8.9$	$9.6$	$9.6$
$S^{2}$	$1.4$	$0.8$	$2.3$	$0.8$