浙江省金华市2025年中考一模数学模拟试题
试卷更新日期:2025-03-05 类型:中考模拟
一、选择题(本题共有10小题,每小题3分,共30分)
-
1. -5的相反数是( )A、-5 B、5 C、 D、-2. 下列运算中,不正确的是( )A、 B、 C、 D、3. 某同学对数据35,29,32,4■,45,45进行统计分析,发现两位数“4■”的个位数字模糊不清,则下列统计量一定不受影响的是( )A、平均数 B、中位数 C、众数 D、方差4. 港珠澳大桥东起香港国际机场附近的香港口岸人工岛,向西横跨伶仃洋海域后连接珠海和澳门人工岛,止于珠海港湾,全长55千米,设计时速100千米/小时,工程项目总投资额1269亿元,用科学记数法表示1269亿元为( )A、1269×108 B、1.269×108 C、1.269×1010 D、1.269×10115. 下列说法中错误的是( )A、两点之间线段最短 B、如果∠α=53°38',那么∠α余角的度数为36°22' C、一个锐角的余角比这个角的补角小 D、互补的两个角一个是锐角一个是钝角6. 如图 所示为一个几何体的三视图, 那么这个几何体的侧面积是( )
 A、 B、 C、 D、7. “a为正数”可以表示为( )A、 B、 C、 D、8. 如图,在数轴上,点、分别表示、 , 且.若、两点之间的距离为6,则点表示的数为( )
A、 B、 C、 D、7. “a为正数”可以表示为( )A、 B、 C、 D、8. 如图,在数轴上,点、分别表示、 , 且.若、两点之间的距离为6,则点表示的数为( ) A、 B、0 C、3 D、9. 在中, , , , 则下列三角函数值不正确的是( )A、 B、 C、 D、10. 如图,在的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则的值为( )
A、 B、0 C、3 D、9. 在中, , , , 则下列三角函数值不正确的是( )A、 B、 C、 D、10. 如图,在的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 当时,分式无意义.12. 一只自由飞行的小鸟,如果随意落在如图所示的方格地面上(每个小方格形状完全相同),那么小鸟落在阴影方格地面上的概率是 .
 13. 小华在计算时(☆代表一个有理数),误将“”看成“”,按照正确的运算顺序计算,结果为 , 则的正确结果是 .14. 如图,矩形中,点M为上一点,过点M作交于点N,将沿折叠得到 , 点B的对应点为点P,连接 , 若 , , 当为以为腰的等腰三角形时,的长为
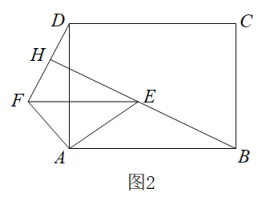
13. 小华在计算时(☆代表一个有理数),误将“”看成“”,按照正确的运算顺序计算,结果为 , 则的正确结果是 .14. 如图,矩形中,点M为上一点,过点M作交于点N,将沿折叠得到 , 点B的对应点为点P,连接 , 若 , , 当为以为腰的等腰三角形时,的长为 15. 如图1,在矩形ABCD中, , , E,F分别为AB,AD的中点,连接EF.如图2,将△AEF绕点A逆时针旋转角 , 使 , 连接BE并延长交DF于点H,则∠BHD的度数为 , DH的长为.
15. 如图1,在矩形ABCD中, , , E,F分别为AB,AD的中点,连接EF.如图2,将△AEF绕点A逆时针旋转角 , 使 , 连接BE并延长交DF于点H,则∠BHD的度数为 , DH的长为.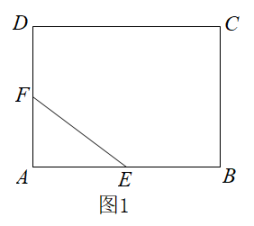
 16. 如图,在矩形中, , , 点是边上的一个动点,将沿折叠,得到 . 连接、 , 若为等腰三角形,则的长为 .
16. 如图,在矩形中, , , 点是边上的一个动点,将沿折叠,得到 . 连接、 , 若为等腰三角形,则的长为 .
三、解答题(本题共8小题,共66分)
-
17. 计算: .18. 如图,在Rt中, , , , 将扩充为等腰三角形 , 使扩充的部分是以为直角边的直角三角形,请用尺规作图画出图形,并求的长.
 19. 某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
19. 某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题: (1)、此次调查抽取了多少用户的用水量数据?(2)、补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;(3)、如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?20. 如图1,是一台小型输送机,其示意图如图2所示.已知两个支架的端点的距离 , 传输带与支架所成的角 , 支架端点离地面的高度 , 求支架端点离地面的高度 . (结果精确到0.1m;参考数据 , , ).
(1)、此次调查抽取了多少用户的用水量数据?(2)、补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;(3)、如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?20. 如图1,是一台小型输送机,其示意图如图2所示.已知两个支架的端点的距离 , 传输带与支架所成的角 , 支架端点离地面的高度 , 求支架端点离地面的高度 . (结果精确到0.1m;参考数据 , , ). 21. 如图,在中, , 以为直径作交于点 , 过点作的垂线交于点 , 交的延长线于点 .
21. 如图,在中, , 以为直径作交于点 , 过点作的垂线交于点 , 交的延长线于点 . (1)、求证:与相切;(2)、若 , , 求的长.
(1)、求证:与相切;(2)、若 , , 求的长.
