贵州省黔东南苗族侗族自治州凯里市凯里学院附属中学2024-2025学年下学期九年级数学第一次月考试卷

试卷更新日期：2025-02-27 类型：月考试卷

进入出卷网下载

一、单选题（每个小题3分，共36分）

1. $2025$ 的倒数是（）

A、 $2025$ B、 $- 2025$ C、 $\frac{1}{2025}$ D、 $- \frac{1}{2025}$

查看试题解析
2. 下图是由一个长方体和一个圆柱组成的几何体，它的俯视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 某年某月某日，我国神舟十六号飞船发射成功，神舟十六号飞船身高9米，重约8吨，飞行速度约每秒7800米，请将数7800用科学记数法表示为（）

A、 $0.78 \times 10^{4}$ B、 $7.8 \times 10^{4}$ C、 $7.8 \times 10^{3}$ D、 $0.78 \times 10^{3}$

查看试题解析
4. 如图，一块直角三角板的直角顶点放在直尺的一边上．如果 $∠ 1 = 70 °$ ，那么 $∠ 2$ 的度数是（　　）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $45 °$

查看试题解析
5. 计算 $\frac{3 x}{x - 1} - \frac{3}{x - 1}$ 的结果等于（）

A、 $3$ B、 $x$ C、 $\frac{x}{x - 1}$ D、 $\frac{3}{x^{2} - 1}$

查看试题解析
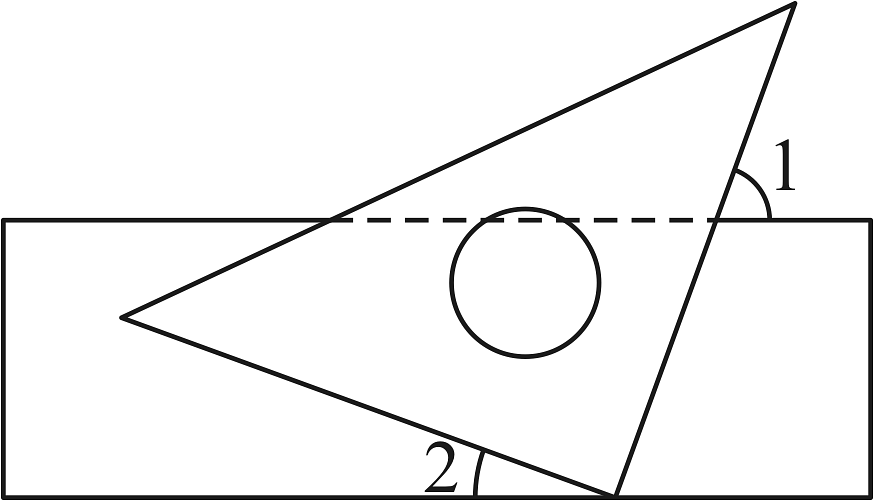6. 某校九年级选出三名同学参加学校组织的“法治和安全知识竞赛”.比赛规定，以抽签方式决定每个人的出场顺序，主持人将表示出场顺序的数字1，2，3分别写在3张同样的纸条上，并将这些纸条放在一个不透明的盒子中，搅匀后从中任意抽出一张，小星第一个抽，下列说法中正确的是（）

A、小星抽到数字1的可能性最小 B、小星抽到数字2的可能性最大 C、小星抽到数字3的可能性最大 D、小星抽到每个数的可能性相同

查看试题解析
7. 如图所示， $△ A B C$ 平移得到 $△ D E F$ ，若 $∠ D E F = 35 °$ ， $∠ A C B = 70 °$ ，则 $∠ A$ 的度数是（）

A、 $55 °$ B、 $65 °$ C、 $75 °$ D、 $85 °$

查看试题解析
8. 如图，在矩形 $A B C D$ 中， $A (- 3, 2), B (3, 2), C (3, - 1)$ ，则D的坐标为（）

A、 $(- 2, - 1)$ B、 $(4, - 1)$ C、 $(- 3, - 2)$ D、 $(- 3, - 1)$

查看试题解析
9. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ 分别在边 $A B$ ， $A C$ 上， $D E$ 与 $B C$ 不平行，添加下列条件之一仍不能判定 $△ A D E ∽ △ A C B$ 的是（　　）

A、 $\frac{A D}{A C} = \frac{A E}{A B}$ B、 $\frac{A E}{A B} = \frac{D E}{B C}$ C、 $∠ A E D = ∠ B$ D、 $∠ A D E = ∠ C$

查看试题解析
10. 在 $Rt △ A B C$ 中， $∠ C = 90 °$ ，以A为圆心，适当长为半径画弧，交 $A C, A B$ 于D，E两点，再分别以D，E为圆心，大于 $D E$ 的长为半径画弧，两弧交于点 $M ．$ 作射线 $A M$ 交 $B C$ 于点F，若 $B F = 5$ ， $B C = 9$ ，则点F到 $A B$ 的距离为（）

A、3 B、4 C、 $4.5$ D、5

查看试题解析
11. 中国古代数学名著《九章算术》中记载：“今有人共买兔，人出七，盈十一；人出五，不足十三，问人数几何？”意思是：“有若干人共同出钱买兔，如果每人出七钱，那么多了十一钱；如果每人出五钱，那么少了十三钱．问：共有几人？”设共有 $x$ 人，根据题意可列方程为（）

A、 $7 x - 11 = 5 x + 13$ B、 $7 x + 11 = 5 x - 13$ C、 $\frac{x - 11}{7} = \frac{x + 13}{5}$ D、 $\frac{x + 11}{7} = \frac{x - 13}{5}$

查看试题解析
12. 如图，抛物线 $y = a x^{2} + c$ 经过正方形 $O A B C$ 的三个顶点A，B，C，点B在 $y$ 轴上，则 $a c$ 的值为（）

A、 $- 1$ B、 $- 2$ C、 $- 3$ D、 $- 4$

查看试题解析

二、填空题（每个小题4分，4个小题，共16分）

13. 计算： $7 a - 4 a =$ ．

查看试题解析
14. 青少年科技创新大赛是一项具有30年历史的全国性青少年科技创新成果和科学探究项目的综合性科技竞赛．某校准备从甲、乙、丙、丁四个科创小组中选出一组参加青少年科技创新大赛．表格反映的是各组平时成绩的平均数 $\bar{x}$ （单位：分），及方差 $s^{2}$ ，如果要选出一个成绩较好且状态稳定的组去参赛，那么应去的组是．
甲
乙
丙
丁
$\bar{x}$
7
8
8
7
$s^{2}$
1
1.2
0.9
1.8

查看试题解析
15. 如图， $△ A B C$ 为等腰三角形， $∠ C = ∠ B = 30 °$ ，点D为 $B C$ 上一点，且 $∠ D A C = 90 °$ ， $A D = 3$ ，则 $B C$ 的长为．

查看试题解析
16. 在矩形 $A B C D$ 中， $A B = 6$ ，点 $E$ 在 $B C$ 上，点 $F$ 在平面内， $B E = 2$ ， $E F = 3$ ，连按 $A F$ ，将线段 $A F$ 绕着点 $A$ 顺时针旋转 $90 °$ 得到 $A P$ ，则线段 $P E$ 的最大值为．

查看试题解析

三、解答题（9个小题，共98分）

17. （1）计算： $\sqrt{9} - 2^{0} + |- 1| - 2 \cos 60 °$ ．
（2）已知 $M = x - 1$ ， $N = 5 x - 6$ ，若 $4 M > N$ ，求 $x$ 的取值范围．

查看试题解析
18. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ，点D为 $A B$ 边上任意一点（不与点A、B重合），过点D作 $D E ∥ B C$ ， $D F ∥ A C$ ，分别交 $A C$ 、 $B C$ 于点E、F，连接 $E F$ ．

(1)、求证：四边形 $E C F D$ 是矩形；

(2)、若 $C F = 2 ， C E = 4$ ，求点C到 $E F$ 的距离．

查看试题解析
19. 2024年12月1日在“跃动南马，壮行天下”的口号下第十六届南宁马拉松比赛正式开跑，这场赛事展示了南宁的城市魅力和文化底蕴．为此学校举办了一次南宁历史知识竞赛，并随机抽取部分学生，将竞赛成绩按以下五组进行整理（得分用x表示）： $A : 50 \leq x < 60, B : 60 \leq x < 70, C : 70 \leq x < 80, D : 80 \leq x < 90, E : 90 \leq x < 100$ ，并绘制出如图的统计图1和图2．
请根据相关信息，解答下列问题：

(1)、本次竞赛抽取学生的人数为__________，并将条形统计图补充完整．

(2)、若“ $90 \leq x < 100$ ”这一组的数据为：90，96，92，95，93，96，96，95，97，100．则这组数据的众数是__________，中位数是__________．

(3)、经过初赛，进入决赛的同学有1名女生和2名男生，现从这三位同学中决出冠亚军，请用列表或画树状图法求冠亚军的两人恰好是一男一女的概率．

查看试题解析
20. 如图，点 $A (n, 6)$ 和 $B (3, 2)$ 是一次函数 $y_{1} = k x + b$ 的图象与反比例函数 $y_{2} = \frac{m}{x} (x > 0)$ 的图象的两个交点．

(1)、求一次函数与反比例函数的表达式；

(2)、当 $x$ 为何值时， $y_{1} > y_{2}$ ？

查看试题解析
21. 在中国进出口商品交易会上，某陶瓷企业出售了A，B两种产品．已知出售1件A产品和2件B产品共收入700元，出售2件A产品和3件B产品共收入1200元．

(1)、求A产品和B产品的单价；

(2)、若出售A，B两种产品（均有销售）共收入1800元，则出售A，B两种产品各几件？

查看试题解析
22. 2024年春节期间，遵义部分县区举办“新春灯会·喜迎龙年”活动，引进了现代光电技术，让古老的彩灯艺术焕发出青春的熠熠光芒．如图是某地灯会现场部分示意图， $A B$ 为主灯塔， $B C$ 为汇展舞台， $C D ⊥ B C$ 于点C，一束灯光的光线从主灯塔A处发出，经过平面镜D处，反射到达舞台中央E处（ $M N$ 为法线）．测得水平方向 $C E = B E = 4 m ， ∠ C E D = 42 °$ ．（参考数据： $\sin 42 ° \approx 0.66$ ， $\cos 42 ° \approx 0.74$ ， $\tan 42 ° \approx 0.9$ 结果保留一位小数）

(1)、求 $C D$ 的高度；

(2)、求主灯塔 $A B$ 的高度．

查看试题解析
23. 如图， $A B$ 是 $⊙ O$ 的直径，E是 $⊙ O$ 上一点， $∠ B A E$ 的平分线 $A C$ 交 $⊙ O$ 于点C，过点C作 $C D ⊥ A E$ 交 $A E$ 的延长线于点D．

(1)、填空： $\overset{⌢}{E C}$ ______ $\overset{⌢}{B C}$ （选填“>”、“<”或“＝”）；

(2)、求证： $C D$ 是 $⊙ O$ 的切线；

(3)、若 $A B = 6 ， ∠ B A C = 30 °$ ，求阴影部分的面积．

查看试题解析
24. 已知二次函数 $y = x^{2} + 2 a x - 4$ （a为常数）．

(1)、若二次函数的图象经过点 $(1, - 5)$ ，求 $a$ 的值；

(2)、在（1）的条件下，当 $- 1 \leq x \leq 4$ 时，请求出二次函数的最大值和最小值；

(3)、当 $0 \leq x \leq 1$ 时，二次函数 $y = x^{2} + 2 a x - 4$ 图象上的点到 $x$ 轴距离的最大值为 $5$ ，求 $a$ 的值．

查看试题解析
25. 如图，在 $Rt △ A B C$ 中， $∠ A B C = 90 ° ， B O$ 为斜边上的高，在射线 $A B$ 上有一点 $M$ ，连接 $O M$ ，作 $∠ M O N = 90 ° ， O N$ 交射线 $B C$ 于点 $N$ ．
【问题发现】
（1）如图甲所示，如果 $A B = C B$ ，则 $O M$ 与 $O N$ 的数量关系 $O M$ ______ $O N$ （填“>”“<”或“=”）；
【类比探究】
（2）如图乙所示，如果改变 $Rt △ A B C$ 中两直角边的比例，使得 $A B = 2 B C$ ，则 $O M$ 与 $O N$ 还存在图甲中的关系吗？说明理由．
【拓展延伸】
（3）如图丙所示，在 $Rt △ A B C$ 中，如果已知 $B C = 2 ， A B = 2 \sqrt{3} ， N O = \sqrt{2}$ ，试求 $B M$ 的长．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	7	8	8	7
$s^{2}$	1	1.2	0.9	1.8