浙江省杭州市拱墅区2024-2025学年八年级上学期数学期末试卷
试卷更新日期:2025-02-25 类型:期末考试
一、选择题:本题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
-
1. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 杭州市秋季某日的最高气温是 , 最低气温是 , 杭州当日气温的变化范围是( )A、 B、 C、 D、3. 木工师傅要做一个三角形木架,有两根木条的长度为7cm和14cm,第三根木条的长度可以是( )A、5cm B、18cm C、21cm
D23cm
4. 一个直角三角形,若三边的平方和为200,则斜边长为( )A、8 B、9 C、10 D、115. 下列说法正确的是( )A、对应角相等的两个三角形是全等三角形 B、一个角等于的三角形是等边三角形 C、等腰三角形两腰上的高相等 D、等腰三角形的角平分线,中线和高重合6. 若 , 则( )A、 B、 C、 D、7. 已知一次函数的图象经过.若 , 则( )A、 B、 C、 D、8. 如图,在中, , 点是边AB上的一个动点,则的度数可能是( ) A、 B、 C、 D、9. 快车从甲地匀速开往乙地,慢车从乙地出发沿同一条公路匀速前往甲地.慢车先出发1小时,快车再出发.设慢车行驶的时间为小时,两车之间的距离为千米,与的函数关系如图所示.下列结论:①快车出发4.4小时后两车相遇;②慢车的速度是100千米/小时;③线段AB所在直线的函数表达式为 , 正确的有( )
A、 B、 C、 D、9. 快车从甲地匀速开往乙地,慢车从乙地出发沿同一条公路匀速前往甲地.慢车先出发1小时,快车再出发.设慢车行驶的时间为小时,两车之间的距离为千米,与的函数关系如图所示.下列结论:①快车出发4.4小时后两车相遇;②慢车的速度是100千米/小时;③线段AB所在直线的函数表达式为 , 正确的有( ) A、①② B、②③ C、①②③ D、①③10. 如图,在中,是BC边上的高线,EF垂直平分AB , 分别交于点.若 , 则( )
A、①② B、②③ C、①②③ D、①③10. 如图,在中,是BC边上的高线,EF垂直平分AB , 分别交于点.若 , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题有6个小题,每小题3分,共18分.
-
11. 在中,已知是三角形(填“锐角”,“直角”或“钝角”)。12. 如图,四盏灯笼的坐标分别是 , 要使四盏灯笼组成的图形关于轴对称,只需把灯笼向右平移个单位.
 13. 如图,在中,边AC的垂直平分线交AC于点 , 交BC于点 , 若的周长为18,则BC的长为.
13. 如图,在中,边AC的垂直平分线交AC于点 , 交BC于点 , 若的周长为18,则BC的长为. 14. 某校开展了“科技节”课外知识竞赛.一共有20道题,每答对一题加5分,不答不扣分,每答错一题倒扣2分.已知小明答错与不答的题数相同,最后比赛得分超过64分.设小明答错了道题,根据题意,可列出关于的不等式为.15. 已知函数.若函数与的图象交于轴上的一点,且函数的图象经过第二,三,四象限,则不等式的解集为.16. 如图,在中,的平分线交BC于点 , 连接AD , 过点作 , 交AC于点 , 过点作 , 交AC于点.若 , 则.
14. 某校开展了“科技节”课外知识竞赛.一共有20道题,每答对一题加5分,不答不扣分,每答错一题倒扣2分.已知小明答错与不答的题数相同,最后比赛得分超过64分.设小明答错了道题,根据题意,可列出关于的不等式为.15. 已知函数.若函数与的图象交于轴上的一点,且函数的图象经过第二,三,四象限,则不等式的解集为.16. 如图,在中,的平分线交BC于点 , 连接AD , 过点作 , 交AC于点 , 过点作 , 交AC于点.若 , 则.
三、解答题:本大题有8个小题,共72分.解答应写出文字说明,证明过程或演算步骤.
-
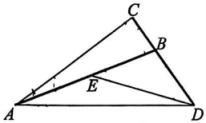
17. 解不等式(组):(1)、;(2)、.18. 如图,在中, , 点 , 点分别在边上,满足 , 连接.
 (1)、求证:.(2)、若 , 求的度数.19. 如图,在平面直角坐标系中,已知点 , 点与点关于轴对称.
(1)、求证:.(2)、若 , 求的度数.19. 如图,在平面直角坐标系中,已知点 , 点与点关于轴对称. (1)、画出点的位置,并求点的坐标.(2)、连接 , 求的面积.(3)、将点向右平移个单位得到点 , 连接CD , 若 , 请你直接写出的值.20. 如图,在中,是斜边AB上的高线,CE是斜边AB上的中线.
(1)、画出点的位置,并求点的坐标.(2)、连接 , 求的面积.(3)、将点向右平移个单位得到点 , 连接CD , 若 , 请你直接写出的值.20. 如图,在中,是斜边AB上的高线,CE是斜边AB上的中线. (1)、若 , 求证:.(2)、若 , 求CD的长.21. 某日上午,甲、乙两车先后从A地出发沿同一条公路匀速前往地(此公路全程速度限定为不超过),地与地的距离为300km.甲车在上午7点离开地,以的速度向地匀速行驶(途中不停靠).设甲车行驶的时间为 , 行驶路程为.(1)、写出关于的函数表达式,并求出甲车到地所需的时间.(2)、已知乙车在当天上午8点出发,以的速度向地匀速行驶(途中也不停靠),请判断甲,乙两车谁先到达地,并说明理由.22. 综合与实践
(1)、若 , 求证:.(2)、若 , 求CD的长.21. 某日上午,甲、乙两车先后从A地出发沿同一条公路匀速前往地(此公路全程速度限定为不超过),地与地的距离为300km.甲车在上午7点离开地,以的速度向地匀速行驶(途中不停靠).设甲车行驶的时间为 , 行驶路程为.(1)、写出关于的函数表达式,并求出甲车到地所需的时间.(2)、已知乙车在当天上午8点出发,以的速度向地匀速行驶(途中也不停靠),请判断甲,乙两车谁先到达地,并说明理由.22. 综合与实践如图,在中,.以点为圆心,AB为半径画弧,交AC于点 , 连接BD.过点作BD的垂线,交BC于点.
观察这个图形,同学们纷纷提出自己的想法.
 (1)、圆圆说:“.”你认为圆圆的说法正确吗?请说明理由.(2)、方方说:“若 , 则.”请你证明结论.(3)、小明说:“给出条件 , 就可以确定的度数.”请你直接写出的度数.
(1)、圆圆说:“.”你认为圆圆的说法正确吗?请说明理由.(2)、方方说:“若 , 则.”请你证明结论.(3)、小明说:“给出条件 , 就可以确定的度数.”请你直接写出的度数.