浙江省金华市义乌宾王中学2024-2025学年九年级第二学期数学开学检测试卷

试卷更新日期：2025-02-25 类型：开学考试

进入出卷网下载

一、填空题（共10题，每题3分，共30分）

1. ⊙O的半径为4cm ，若点P到圆心的距离为4cm ，点P在（）

A、圆内 B、圆上 C、圆外 D、无法确定

查看试题解析
2. 下列事件中，不可能事件（）

A、任意选择某一电视频道，它正播放动画片 B、任意掷一枚硬币，正面朝上 C、在只装有红球的袋子里摸出一个黑球 D、射击运动员射击一次，命中10环

查看试题解析
3. 已知 $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a + b}{b}$ 的值为（）

A、 $\frac{5}{2}$ B、 $\frac{5}{3}$ C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
4. 将二次函数y＝2x²的图象先向下平移3个单位，再向左平移4个单位所得图象的解析式为（）

A、y＝2（x﹣4）²+3 B、y＝2（x+4）²﹣3 C、y＝2（x+4）²+3 D、y＝2（x﹣4）²﹣3

查看试题解析
5. 如图，点A、B、C在⊙O上，∠ACB＝40°，弧AB的度数为（）

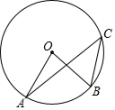A、80° B、40° C、20° D、60°

查看试题解析
6. 如图，已知AD为△ABC中BC边上的中线，过重心G作GE∥AC，交BC于点E，DE＝2，则BC的长为（）

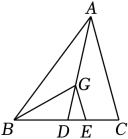A、12 B、8 C、6 D、4

查看试题解析
7. 如图是二次函数y＝ax²+bx+c的图象，则不等式ax²+bx+c＜3的解集是（）

A、x＜0 B、x＜﹣1或x＞3 C、0＜x＜2 D、x＜0或x＞2

查看试题解析
8. 如图， $△ A B C$ 中， $A B = 3$ ，将 $△ A B C$ 绕点 $A$ 逆时针旋转 $60 °$ 得到 $△ A B_{1} C_{1}$ ， $A B_{1}$ 恰好经过点 $C .$ 则阴影部分的面积为（）

A、 $\frac{2}{3} π$ B、 $\frac{3}{2} π$ C、 $\frac{4}{3} π$ D、 $\frac{3}{4} π$

查看试题解析
9. 如图，已知抛物线y＝ax²+bx+c（a≠0）交x轴于点A（﹣1，0）和x轴正半轴于点B ，且BO＝3AO ，交y轴正半轴于点C ．有下列结论：①abc＞0；②2a+b＝0；③x＝1时y有最大值﹣4a；④3a+c＝0．其中，正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
10. “青朱出入图”是东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法．如图，四边形ABCD ， BEFG ， ECHI均是正方形，A ， B ， E三点共线，CE与FG交于点J ， HI与AB交于点K ，连结KJ ，交BC于点P ，若△EJK与△CHD的面积比为10：9，则BP：CP的值是（）

A、 $\frac{7}{20}$ B、 $\frac{15}{34}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{\sqrt{10}}{10}$

查看试题解析

二、填空题（共6题，每题3分，共18分）

11. 二次函数y＝x²﹣1图象的顶点坐标是.

查看试题解析
12. 已知线段AB＝2，点P是线段AB的黄金分割点，那么较长线段AP＝．

查看试题解析
13. 如图，圆锥的底面半径OC＝5，高AO＝12，则该圆锥的侧面积等于．

查看试题解析
14. 如图，在 $∆ A B C$ 中，∠C=90⁰ ， AC=10cm，BC=8cm，点P从点C出发，以 $2 c m / s$ 的速沿着 $C A$ 向点A匀速运动，同时点Q从点B出发，以 $1 c m / s$ 的速度沿 $B C$ 向点C匀速运动，当一个点到终点时，另一个点随之停止.经过秒后， $△ P C Q$ 与 $△ A B C$ 相似.

查看试题解析
15. 如图，Rt△ABC的斜边AB与⊙O相切于点D ， ⊙O与BC交于点E ，连接DE ， DE∥AC ．已知BE＝EC＝ $\sqrt{2}$ ， AC＝4，则⊙O的直径为．

查看试题解析
16. 准备在一个“7”字型遮阳棚下安装一个喷水装置（如图1），已知遮阳棚DB与竖杆OB垂直，遮阳棚的高度OB＝3米，喷水点A与地面的距离OA＝1米（喷水点A喷出来的水柱呈抛物线型），水柱喷水的最高点恰好是遮阳棚的C处，C到竖杆的水平距离BC＝2米（如图2），此时水柱的函数表达式为，现将遮阳棚BD绕点B向上旋转45°（如图3），则此时水柱与遮阳棚的最小距离为米．（保留根号）

查看试题解析

三、解答题（17-21每题8分，22、23每题10分，24题12分）

17. 计算： ${(\frac{1}{3})}^{- 1} + | 1 - \sqrt{2} | - 2 c o s 4 5^{∘}$ ．

查看试题解析
18. 寒假，明明、亮亮准备去哈尔滨旅游，游玩以下三个景点：“冰雪大世界”、“东北虎林园”、“太阳岛风景区”，假设游玩的顺序是随机的．

(1)、“冰雪大世界”作为游玩的第一个景点的概率是；

(2)、求游玩顺序为“冰雪大世界”→“东北虎林园”→“太阳岛风景区”的概率．

查看试题解析
19. 如图，在△ABC中，延长CB至点D ，使BD＝BC ，在AC上取一点F ，连接DF交AB于点E ，过F点作FH∥AB交CD于点H ，已知AC＝DE＝3，EF＝2．

(1)、DB：DH =

(2)、求AF的长．

查看试题解析
20. 在数学综合实践活动课上，某小组要测量学校升旗台旗杆的高度．如图所示，测BC∥AD ，斜坡AB的长为6m ，坡度i＝1： $\sqrt{3}$ ，在点B处测得旗杆顶端E的仰角为70°，点B到旗杆底端C的距离为4 m ．

(1)、求斜坡AB的坡角α的度数．

(2)、求旗杆顶端离地面的高度ED ．（参考数据sin70°≈0.94，cos70°≈0.34，tan70°≈2.75，结果精确到1m）

查看试题解析
21. 如图，在8×8的正方形网格中， $△ A B C$ 的三个顶点都在格点上，请按要求完成下列作图：①仅用无刻度直尺，且不能用直尺中的直角；②保留作图痕迹.

(1)、在图甲中，画出 $△ A B C$ 的BC边上的中线AD.

(2)、在图乙中，找一点 $P$ ，连结线段BP，使得BP平分 $∠ A B C$ .

查看试题解析
22. 如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．

(1)、试判断直线BC与⊙O的位置关系，并说明理由；

(2)、若BD= $\sqrt{3}$ BF，AC=3，求阴影部分的面积（结果保留π）．

查看试题解析
23. 已知二次函数y＝ax²﹣2ax+b（a≠0）的图象经过点（﹣2，0）．

(1)、求a和b的关系式；

(2)、当﹣3≤x≤2时，函数y有最小值﹣3，求a的值；

(3)、若a＝﹣1时，将函数图象向上平移m（m＞0）个单位长度，图象与x轴相交于点A ， B（点A在y轴的左侧）．当 $\frac{A O}{B 0} = \frac{2}{3}$ 时，求m的值．

查看试题解析
24. 如图，已知AB为⊙O的直径，弦CD⊥AB于点E ， G是 $\overset{⌢}{A C}$ 上的动点，连结AD ， AG ， DG ， CG.DG与AB交于点P，延长AG ， DC相交于点F。

(1)、求证：∠ADG＝∠F；

(2)、已知CD= $\frac{3}{5}$ AB
①若AB=10，tan∠F= $\frac{3}{4},$ 求△CGF的周长；
②在点G的运动过程中，当△APG成为以AP为腰的等腰三角形时，求 $\frac{G F}{G C}$ 的值．

查看试题解析