浙江省杭州市萧山区2025年中考一模数学模拟试题
试卷更新日期:2025-02-25 类型:中考模拟
一、选择题:本题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 的相反数是( )A、 B、 C、2023 D、-20232. 据报道,浙江省举全省之力筹办杭州亚运会,共有37600名志愿者参加.其中37600用科学记数法可表示为( )A、 B、 C、 D、3. 下列立体图形中,主视图是圆的是( )A、
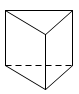 B、
B、 C、
C、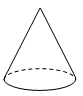 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 数学小组对校足球社团的20名成员进行年龄调查结果如图所示。其中有部分数据被墨迹遮挡,关于这20名成员年龄的统计量,仍能够分析得出的是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 数学小组对校足球社团的20名成员进行年龄调查结果如图所示。其中有部分数据被墨迹遮挡,关于这20名成员年龄的统计量,仍能够分析得出的是( ) A、平均数 B、众数 C、中位数 D、方差6. 已知为直线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 如图, , E为的中点,与相交于点F, , 则的度数是( )
A、平均数 B、众数 C、中位数 D、方差6. 已知为直线上的三个点,且 , 则以下判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 如图, , E为的中点,与相交于点F, , 则的度数是( ) A、56° B、62° C、63° D、72°8. 如图,是的内接三角形,AD是的直径,若 , 则图中阴影部分的面积为( )
A、56° B、62° C、63° D、72°8. 如图,是的内接三角形,AD是的直径,若 , 则图中阴影部分的面积为( ) A、 B、 C、 D、9. 将抛物线向下平移3个单位,再向右平移3个单位后的解析式为( )A、 B、 C、 D、
A、 B、 C、 D、9. 将抛物线向下平移3个单位,再向右平移3个单位后的解析式为( )A、 B、 C、 D、二、填空题:本题有6个小题,每小题3分,共18分.
-
10. 因式分解:3m2-12= .11. 在不透明袋子里装有颜色不同的8个球,这些球除颜色外完全相同.每次从袋子里摸出1个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.25,估计袋中白球有个.12. 如图, , 平分 , , , 则的度数是 .
 13. 圣诞节时,某班一个小组有x人,他们每两人之间互送贺卡一张,已知全组共送贺卡110张,则可列方程为 .14. 在平面直角坐标系中,关于x的函数y=-x+3a+2和y=x2-ax的图象相交于点P、Q.(1)、若点P的横坐标为1,则a= .(2)、若P、Q两点都在x轴的上方,且a≠0,则实数a的取值范围是 .15. 如图,内接于 , 点在上,平分交于 , 连结 . 若 , , 则的长为 .
13. 圣诞节时,某班一个小组有x人,他们每两人之间互送贺卡一张,已知全组共送贺卡110张,则可列方程为 .14. 在平面直角坐标系中,关于x的函数y=-x+3a+2和y=x2-ax的图象相交于点P、Q.(1)、若点P的横坐标为1,则a= .(2)、若P、Q两点都在x轴的上方,且a≠0,则实数a的取值范围是 .15. 如图,内接于 , 点在上,平分交于 , 连结 . 若 , , 则的长为 .
三、解答题:本题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤.
-
16.(1)、解方程:(2)、先化简,再求值: , 其中 .17. 合并同类项:(1)、;(2)、;(3)、 .18. 在开展“双减”活动期间,某市教育部门为了解八年级学生每 学期参加综合实践活动的情况,随机抽样调查了本市内八年级学生一个学期参加综合实践活 动的天数,并用得到的数据绘制了下面两幅不完整的统计图如下: 请你根据图中提供的信息,回答下列问题:
 (1)、补全条形统计图.(2)、通过计算估计该市八年级学生每学期参加综合实践活动的平均天数约是多少天?(3)、如果该市共有八年级学生5000人,请估计“活动时间不少于5天”的大约有多少人?19. 【背景】在一次物理实验中,小冉同学用一个固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R,RL之间关系为 , 通过实验得出如下数据:
(1)、补全条形统计图.(2)、通过计算估计该市八年级学生每学期参加综合实践活动的平均天数约是多少天?(3)、如果该市共有八年级学生5000人,请估计“活动时间不少于5天”的大约有多少人?19. 【背景】在一次物理实验中,小冉同学用一个固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R,RL之间关系为 , 通过实验得出如下数据:R(Ω)
…
1
a
3
4
6
…
I(A)
…
4
3
2.4
2
b
…
(1)、a= , b=.(2)、【探究】根据以上实验,构建出函数 , 结合表格信息,探究函数的图象与性质.①在平面直角坐标系中画出对应函数的图象.

②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)、【拓展】结合(2)中函数图象分析,当0时,的解为.20. 如图,菱形的对角线与交于点O, , . (1)、求证:四边形是矩形;(2)、若 ,求四边形的周长.21. 在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m , n为实数).(1)、求函数图象的对称轴;(2)、若m , n异号,求证:函数y的图象与x轴有两个不同的交点;(3)、已知当x=0,3,4时,对应的函数值分别为p , q , r , 若2q<p+r , 求证:m<0.22. 问题:如何将物品搬过直角过道?
(1)、求证:四边形是矩形;(2)、若 ,求四边形的周长.21. 在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m , n为实数).(1)、求函数图象的对称轴;(2)、若m , n异号,求证:函数y的图象与x轴有两个不同的交点;(3)、已知当x=0,3,4时,对应的函数值分别为p , q , r , 若2q<p+r , 求证:m<0.22. 问题:如何将物品搬过直角过道?情景:图1是一直角过道示意图,O,P为直角顶点,过道宽度都是.矩形ABCD是某物品经过该过道时的俯视图,宽AB为.
操作:
步骤
动作
目标
1
靠边
将如图1中矩形ABCD的一边AD靠在SO上
2
推移
矩形ABCD沿SO方向推移一定距离,使点在边AD上
3
旋转
如图2,将矩形ABCD绕点旋转
4
推移
将矩形ABCD沿OT方向继续推移

探究:(1)、如图2,已知BC=1.6m,OD=0.6m.小明求得后,说:“ , 该物品能顺利通过直角过道.”你赞同小明的结论吗?请通过计算说明.(2)、如图3,物品转弯时被卡住(分别在墙面PQ与PR上),若.求OD的长.(3)、求该过道可以通过的物品最大长度,即求BC的最大值(精确到0.01米,).23. 等腰三角形AFG中AF=AG,且内接于圆O,D、E为边FG上两点(D在F、E之间),分别延长AD、AE交圆O于B、C两点(如图1),记∠BAF=α,∠AFG=β. (1)、求∠ACB的大小(用α,β表示);(2)、连接CF,交AB于H(如图2).若β=45°,且BC×EF=AE×CF.求证:∠AHC=2∠BAC;(3)、在(2)的条件下,取CH中点M,连接OM、GM(如图3),若∠OGM=2α-45°,①求证:GM∥BC,GM=BC②请直接写出的值.
(1)、求∠ACB的大小(用α,β表示);(2)、连接CF,交AB于H(如图2).若β=45°,且BC×EF=AE×CF.求证:∠AHC=2∠BAC;(3)、在(2)的条件下,取CH中点M,连接OM、GM(如图3),若∠OGM=2α-45°,①求证:GM∥BC,GM=BC②请直接写出的值.