浙江省金华第五中学2024-2024学年九年级第二学期数学期初作业检查试卷

试卷更新日期：2025-02-25 类型：开学考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分．每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1. 已知⊙O的半径为3，点P在圆外，则OP的长度可能为（）

A、4 B、3 C、2 D、1

查看试题解析
2. 抛物线 $y ＝ x^{2} - 9$ 与y轴的交点坐标为（）

A、（-3，0） B、（3，0） C、（0，-9） D、（0，9）

查看试题解析
3. 如图是一个机械零部件，其俯视图为（）

A、 B、 C、 D、

查看试题解析
4. 已知圆心角为120°的扇形的半径为6，则扇形的弧长为（）

A、2π B、4π C、12π D、24π

查看试题解析
5. 如图是5张背面都相同的扑克牌，将其打乱顺序，背面朝上放在桌面上，从中随机抽取一张，抽到的花色可能性最大的是（）

A、♦ B、♠ C、♥ D、♣

查看试题解析
6. 如图，直线l₁//l₂//l₃ ， AC分别交l₁ ， l₂ ， l₃于点A ， B ， C；DF分别交l₁ ， l₂ ， l₃于点D ， E ， F ．若DE＝3，EF＝6，AB＝4，则AC的长为（）

A、6 B、8 C、9 D、12

查看试题解析
7. 如图，AB是半圆O的直径，点C在半圆上，CD是半圆的切线，OD⊥AB ，若∠CAB＝26°，则∠D的度数为（）

A、38° B、45° C、52° D、64°

查看试题解析
8. 已知二次函数 $y ＝ a x^{2} + b x (a \neq 0)$ 图象上部分点的坐标（x ， y）对应值列表如下：
x
…
-3
0
2
…
y
…
15
0
0
…
则关于x的方程 $a x^{2} + b x ＝ 15$ 的解为（）

A、 $x_{1} ＝ - 3$ ， $x_{2} ＝ 5$ B、 $x_{1} ＝ - 3$ ， $x_{2} ＝ 3$ C、 $x_{1} ＝ 0$ ， $x_{2} ＝ 2$ D、 $x_{1} ＝ - 2$ ， $x_{2} ＝ 2$

查看试题解析
9. 如图1是圆形干果盘，其示意图如图2所示，四条隔板AB ， CD ， EF ， GH长度相等，横纵隔板互相垂直交于隔板的三等分点，测得AB＝30cm，则该干果盘的半径为（）

A、 $5 \sqrt{10}$ cm B、 $10 \sqrt{2}$ cm C、 $10 \sqrt{3}$ cm D、 $10 \sqrt{10}$ cm

查看试题解析
10. 如图，将Rt△ABC以直角顶点C为旋转中心，按顺时针方向旋转90°得到Rt△DEC ，延长AB ，交DE于点F ，设 $t a n A ＝ k$ ，则 $\frac{B F}{E F}$ 的值为（）

A、 $1 - k$ B、 $k$ C、 $\frac{1 + k}{1 - k}$ D、 $\frac{1 - k}{1 + k}$

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

11. 若 $\frac{a}{b} ＝ \frac{5}{2}$ ，则 $\frac{a + b}{b}$ 的值为．

查看试题解析
12. 如图，圆锥的底面半径为4cm，母线长为6cm，则圆锥的侧面积为．

查看试题解析
13. 如图是小华用计算机模拟随机投掷一枚图钉的实验结果，若再次抛掷一枚图钉，则可以估计“钉尖向上”的概率是．（精确到0.001）

查看试题解析
14. 如图，在△ABC中，∠C＝90°，D为边BC上的一点，BD＝2CD ， AB＝9， $s i n B = \frac{2}{3}$ ．则AD= ．

查看试题解析
15. 如图，扇形AOB的圆心角∠AOB＝90°，半径OA＝6，点D是 $\overset{⌢}{A B}$ 上一点．AE⊥AO交OD的延长线于点E ， BG⊥OB交OE于点G ．若DE＝4，则BG＝．

查看试题解析
16. 已知点A（ $m$ ， $2 m$ ）（ $m > 2$ ）是二次函数 $y ＝ a x^{2} + k$ （ $a > 0$ ）图象上一点，当 $m - 4 ≤ x ≤ m$ 时，二次函数的最大值和最小值分别为6和 $- 2$ ，则 $a$ 的值为．

查看试题解析

三、解答题（本题有8小题，共72分，解答需写出必要文字说明、演算步骤或证明过程）

17.

(1)、计算：2cos60°－tan45°．

(2)、已知比例式 $x : 3 ＝ 4 : 5$ ，求x的值．

查看试题解析
18. 现有A，B，C，D四张印有青铜器的卡片，卡片除图案外其它均相同．将四张卡片背面朝上，洗匀后放在桌面上，小明从中随机抽取一张，记录图案后不放回，再抽取一张．
后母戊鼎
A
四羊青铜方尊
B
马踏飞燕
C
长信宫灯
D

(1)、请用列表或画树状图的方法，表示所有可能出现的结果．

(2)、求小明抽到的两张卡片中恰好有马踏飞燕的概率．

查看试题解析
19. 如图，在四边形ABCD中，AC平分∠BAD ，且 $A C^{2} ＝ A B \cdot A D$ ．

(1)、求证：△ABC∽△ACD ．

(2)、若∠BCD＝150°，求∠BAC的度数．

查看试题解析
20. 如图，游乐园计划在点O处安装一个高3m的喷水头OA ，使得喷出的水柱正好落到距离O点10m处的B点，且在距离O点4m处达到最高．已知水柱的形状是抛物线的一部分，现以点O为原点建立如图所示直角坐标系．

(1)、求抛物线的函数表达式．

(2)、求出水柱的最高点的高度．

查看试题解析

21. 尺规作图问题：在⊙O中作一个度数为150°的圆心角．

以下是小华的作图过程，他分两步完成，如图所示：

第一步：以⊙O上一点A为圆心，OA长为半径作弧，交

⊙O于点B ，连结OB ．

第二步：分别以A ， B为圆心，大于线段OA长度的长为

半径作圆弧交于圆内一点C ，连结OC并延长交

⊙O于点D ．

则∠AOD即为所求的圆心角．

请根据他的作图过程回答以下问题：

(1)、求∠AOB的度数．

(2)、说明∠AOD的度数为150°的理由．

查看试题解析

22. 综合实践：测量铜像高度．
工具准备：边长为100cm且一边带有刻度的正方形硬纸板、量角器．
测量步骤：如图，将正方形硬纸板ABCD斜放在地面上，使得C ， B ， G三点在同一直线上，将点D对准点G ，视线DG经过边AB上一点F ，读取AF＝10cm，测得 $∠ D C E ＝ 69 °$ ．
查阅数据：sin69°≈0.93，cos69°≈0.36，tan69°≈2.61．
计算结果：

(1)、求CG的长度．

(2)、求铜像的高度GH ．

查看试题解析
23. 点A（ $- 1$ ， b）是抛物线 $y ＝ a x^{2} - 2 x - 11$ 与直线 $y ＝ 3 x - 5$ 的一个交点．

(1)、求a ， b的值及抛物线的对称轴．

(2)、设点B（ $x_{1}$ ， $m$ ）是抛物线上一点，点D（ $x_{2}$ ， $n$ ）是直线 $y ＝ 3 x - 5$ 上一点．
①若 $x_{1} ＝ x_{2}$ ，求 $n - m$ 的最大值．
②若C（ $x_{3}$ ， $m$ ）也是抛物线上的一点，且m $＝$ n ， $x_{2} - x_{1} ＝ x_{3} - x_{2}$ ，求 $m$ 的值．

查看试题解析
24. 如图，四边形ABCD是圆内接四边形，连结AC ， BD交于点E ，过点C作CF∥BD交AD的延长线于点F ．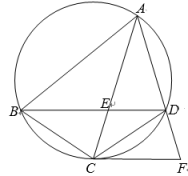

(1)、【认识图形】
求证 $：$ ∠BCA＝∠F ．

(2)、求证 $：$ △ABC∽△CDF ．

(3)、【探索关系】
当点B ， F关于AC对称时．
①若BC＝3，AF＝5，求DE的长．
②记 $\frac{B C}{A F} ＝ x$ ， $\frac{D E}{B E} ＝ y$ ，直接写出y关于x的函数表达式．

查看试题解析

x	…	-3	0	2	…
y	…	15	0	0	…